苏科版八年级上册数学期中考试测试题 4页

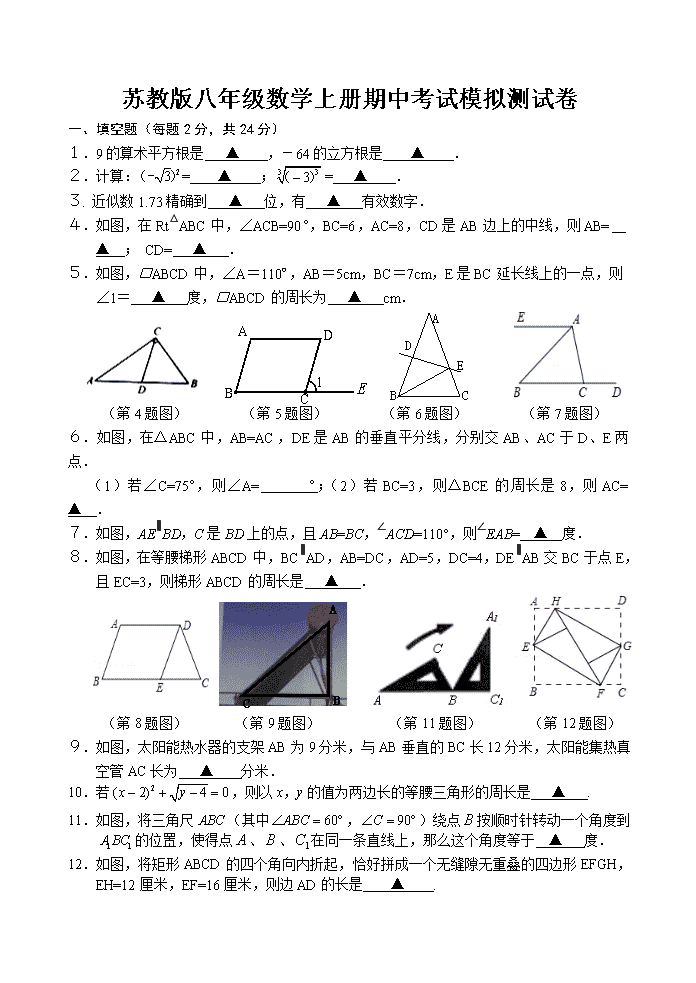
苏教版八年级数学上册期中考试模拟测试卷 一、填空题（每题 2 分，共 24 分） １．9 的算术平方根是 ▲ ，－64 的立方根是 ▲ ． ２．计算： 23（- ）= ▲ ； 3 33（ ） = ▲ ． ３. 近似数 1.73 精确到 ▲ 位，有 ▲ 有效数字． ４．如图，在 Rt△ABC 中，∠ACB=90，BC=6，AC=8，CD 是 AB 边上的中线，则 AB= ▲ ； CD= ▲ ． ５．如图，□ABCD 中，∠A＝110º，AB＝5cm，BC＝7cm，E 是 BC 延长线上的一点，则 ∠1＝ ▲ 度，□ABCD 的周长为 ▲ cm． （第 4 题图） （第 5 题图） （第 6 题图） （第 7 题图） ６．如图，在△ABC 中，AB=AC，DE 是 AB 的垂直平分线，分别交 AB、AC 于 D、E 两点． （1）若∠C=75，则∠A= ；（2）若 BC=3，则△BCE 的周长是 8，则 AC= ▲ ． ７．如图，AE∥BD，C 是 BD 上的点，且 AB=BC，∠ACD=110°，则∠EAB= ▲ 度． ８．如图，在等腰梯形 ABCD 中，BC∥AD，AB=DC，AD=5，DC=4，DE∥AB 交 BC 于点 E，且 EC=3，则梯形 ABCD 的周长是 ▲ ． （第 8 题图） （第 9 题图） （第 11 题图） （第 12 题图） ９．如图，太阳能热水器的支架 AB 为 9 分米，与 AB 垂直的 BC 长 12 分米，太阳能集热真 空管 AC 长为 ▲ 分米． 10．若 2( 2) 4 0x y    ，则以 x，y 的值为两边长的等腰三角形的周长是 ▲ . 11．如图，将三角尺 ABC （其中 60ABC   ， 90C   ）绕点 B 按顺时针转动一个角度到 1 1A BC 的位置，使得点 A 、 B 、 1C 在同一条直线上，那么这个角度等于 ▲ 度． 12．如图，将矩形 ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形 EFGH， EH=12 厘米，EF=16 厘米，则边 AD 的长是 ▲ . 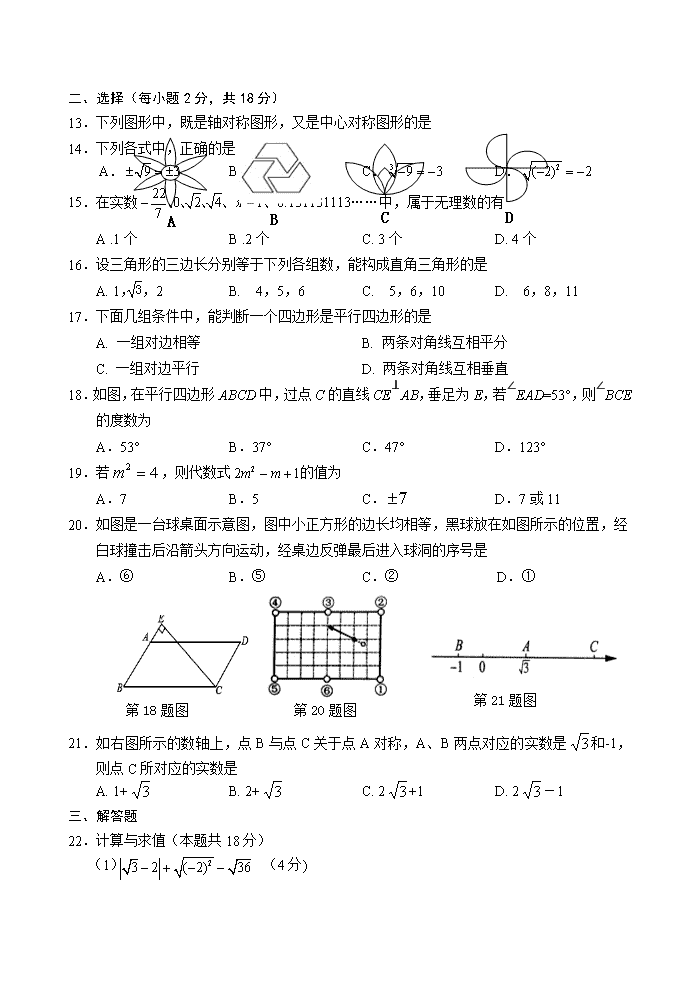二、选择（每小题 2 分，共 18 分） 13．下列图形中，既是轴对称图形，又是中心对称图形的是 A B C D A BC A B C D E E 14．下列各式中，正确的是 A． 9 3   B． 2( 2) 4  C． 3 9 3   D． 2( 2) 2   15．在实数 22 0 2 4 17  、、 、 、 、0.131131113……中，属于无理数的有 A .1 个 B .2 个 C. 3 个 D. 4 个 16．设三角形的三边长分别等于下列各组数，能构成直角三角形的是 A. 1，3，2 B. 4，5，6 C. 5，6，10 D. 6，8，11 17．下面几组条件中，能判断一个四边形是平行四边形的是 A. 一组对边相等 B. 两条对角线互相平分 C. 一组对边平行 D. 两条对角线互相垂直 18．如图，在平行四边形 ABCD 中，过点 C 的直线 CE⊥AB，垂足为 E，若∠EAD=53°，则 ∠BCE 的度数为 A．53° B．37° C．47° D．123° 19．若 2 4m  ，则代数式 22 1m m  的值为 A．7 B．5 C． 7 D．7 或 11 20．如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经 白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是 A．⑥ B．⑤ C．② D．① 21．如右图所示的数轴上，点 B 与点 C 关于点 A 对称，A、B 两点对应的实数是 3 和-1， 则点 C 所对应的实数是 A. 1+ 3 B. 2+ 3 C. 2 3 +1 D. 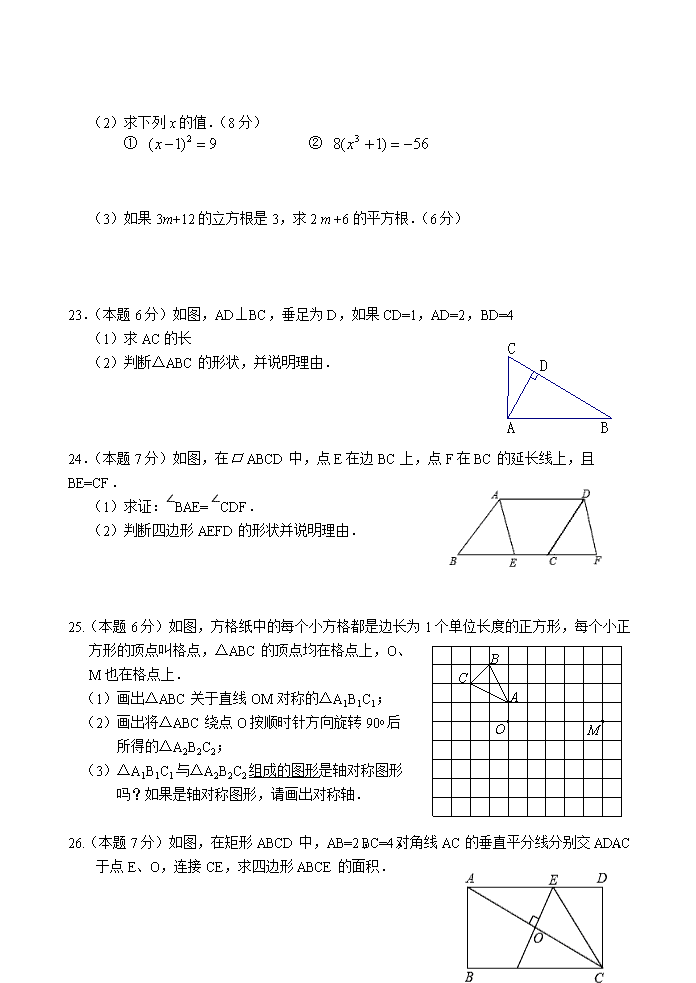2 3 －1 三、解答题 22．计算与求值（本题共 18 分） （1） （4 分) （2）求下列 x 的值．（8 分） 23 2 ( 2) 36    第 18 题图 第 20 题图 第 21 题图 ① 2( 1) 9x   ② 56)1(8 3 x （3）如果 3m+12 的立方根是 3，求 2 m +6 的平方根．（6 分） 23．（本题 6 分）如图，AD⊥BC，垂足为 D，如果 CD=1，AD=2，BD=4 （1）求 AC 的长 （2）判断ΔABC 的形状，并说明理由． 24．（本题 7 分）如图，在口 ABCD 中，点 E 在边 BC 上，点 F 在 BC 的延长线上，且 BE=CF． （1）求证：∠BAE=∠CDF． （2）判断四边形 AEFD 的形状并说明理由． 25.（本题 6 分）如图，方格纸中的每个小方格都是边长为 1 个单位长度的正方形，每个小正 方形的顶点叫格点，△ABC 的顶点均在格点上，O、 M 也在格点上． （1）画出△ABC 关于直线 OM 对称的△A1B1C1； （2）画出将△ABC 绕点 O 按顺时针方向旋转 90o 后 所得的△A2B2C2； （3）△A1B1C1 与△A2B2C2 组成的图形是轴对称图形 吗？如果是轴对称图形，请画出对称轴． 26.（本题 7 分）如图，在矩形 ABCD 中，AB=2，BC=4，对角线 AC 的垂直平分线分别交 AD、AC 于点 E、O，连接 CE，求四边形 ABCE 的面积． D C B A A C B O M 图 1 图 2 27.（本题 7 分）如图 1，在梯形 ABCD 中，AB∥CD，∠BCD＝90O，这样的梯形称作直角梯 形．在该梯形中 AB＝AD＝10cm，BC＝8cm． (1) 求 CD 的长； （2）若点 P 从点 A 出发，以每秒 2cm 的速度沿折线 AB 方向运动，点 Q 从点 D 出发， 以每秒 3cm 的速度沿线段 DC 方向向点 C 运动．已知动点 P、Q 同时发，当点 P 运 动到点 B 时，P、Q 运动停止，设运动时间为 t．①当 t 为何值时，四边形 PBQD 为 平行四边形．②是否存在某一时刻 t，使四边形 APQD 为直角梯形。若存在求出 t 的值；若不存在，说明理由． 28. （本题 7 分） 我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角 线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边． （1）写出你所了解的特殊四边形中是勾股四边形的两种图形的名称 ▲ ， ▲ ； （2）如图 28（1），已知格点（小正方形的顶点） (0 0)O ， ， (3 0)A ， ， (0 4)B ， ，请你画出 以格点为顶点，OA OB， 为勾股边且对角线相等的勾股四边形OAMB ； （3）如图 28（2），将 ABC△ 绕顶点 B 按顺时针方向旋转 60，得到 DBE△ ，连结 AD DC、 ， 30DCB  ∠ ．求证： 2 2 2DC BC AC  ，即四边形 ABCD 是勾股四边形． y B O A x 图 28（1）