八年级数学上册第12章一次函数12-3一次函数与二元一次方程课件（新版）沪科版 23页

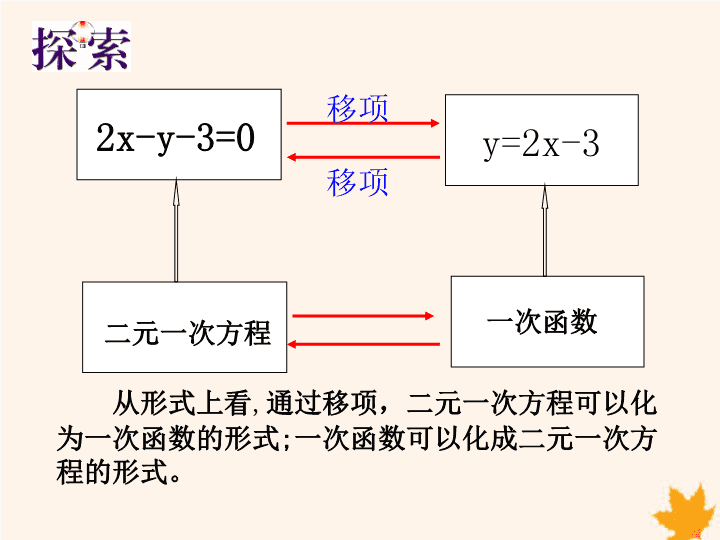
12.3 一次函数与二元一次方程 第十二章 1. 一次函数y=2x-5的图象是 ，通常过（ ，0 ）、 （0， ）两点画直线即可. 一条直线 2.5 -5 2.在下列各组一次函数中，图象是相互平行的直线的一组是 （ ） （A） y=4x-4和y=-4x+4 （B） y=2x-3和y=2x+7 （C） y=3x-1和y=-2x-4 （D）y=4x-1和y= x+5 B 3 2  那么,其他各组的两条直线的位置关系是 .相交 回顾 复习 2x-y-3=0 y=2x-3 移项 移项 二元一次方程 一次函数 从形式上看,通过移项，二元一次方程可以化 为一次函数的形式;一次函数可以化成二元一次方 程的形式。 把下列二元一次方程写成y=kx＋b的形式： (1)3x＋y=7 (2)3x＋2y=6 解:(1) y=－3x+7 (2) 移项 得:2y=－3x+6 y= x+3- 2 3 思考： • 方程3x+2y=6的解有多少个？你能画出以这 个方程的解为坐标的所有点组成的图象吗？ • 我们把方程3x+2y=6化成一次函数的形式 • • 对于这个函数，任意给出自变量x的一些值， 可以求得相应的y值，列表如下 y= x+3- 2 3 …－1.501.534.567.5… …3210－1－2－3…x y= x+3- 3 2 思考： • 表中每一对x、y的值代入 方程3x+2y=6都成立，所 以每组有序数对都是方程 3x+2y=6的解. • 以这些有序数对为坐标， 在坐标平面内找出点作图， 就得到直线3x+2y=6. • 1 2 3 4 5 6 7 o 4321-1-2-3-4 x -1 -2 -3 -4 -5 8 3x+2y=6 由上可知，以二元一次方 程3x+2y=6的每组解为坐 标的点都在直线y= x+3 上.直线y= x+3 上点的 坐标所对应的数组都是方 程3x+2y=6的解. - 3 23- 2 y 二元一次方程kx-y+b=0的解与一次函数y=kx+b图 象上的点有什么关系？ 你认为应如何表述? 一般地，一次函数y=kx＋b的图象上 任意一点的坐标都是二元一次方程kx- y+b=0 的一个解; 以二元一次方程kx－y＋b=0的解为坐 标的点都在一次函数y=kx＋b的图象上. 把下列二元一次方程转化成一次函数的形式. 0)1(  yx 0)2(  yx 63)3(  yx 01054)4(  yx xy  xy  63  xy 2 5 4  xy 63  yx下面有序数对，哪个是二元一次方程 的解？（即哪个点在函数 63  xy 的图象上？） A（2，0）、B（3，－3）、C（5，-9）、 D（6，-10）、E（-2，10）、F（-3、15） Ø点A、点B、点C、点F 一般地，任何一个二元一次方程都 可以转化为一次函数的形式，所以每个二 元一次方程都对应一条直线. 通过以上回顾我们可以得出如下结论： 下面我们就利用图象来探究二元一次 方程组的解法. 两个一次函数表达式可以写成 一个二元一次方程组 这两个一次函数的图象 问题?? 相应的二元一次方程组的解与 有什么关系？ 问题： 1.一次函数图象与二元一次方程有何关系. 2.在同一个直角坐标系中，画出下列一次函数的图象. 22)1(  yx 62)2(  yx 3.两条直线有交点吗？ 写出交点的坐标P（ ） 检验点P的坐标是不是方程组      62 22 yx yx 的解？ 22yx1 ：l 622  yxl ： －2，2 （－2，2） 通过上面的验证，我们发现这两条直线的交点 坐标就是这个方程组的解你能说出其中的道理吗？ 直线 1l 是一次函数 22  yx 图象，因此，直线 1l 上的任意 一点的坐标都是方程 的解；同理，直线 2l 上的每个点的 坐标都是方程 62  yx 的解.所以直线 1l 与 2l 的交点P的 坐标就是方程 22  yx 与 62  yx 的公共解.      62 22 yx yx 也就是二元一次方程组 的解. 这就是利用作图象求解二元一次方程组的方法，由此 我们发现数和形有着密不可分的联系. 22  yx 例1 利用图象解法解方程组      12 1 yx yx ② ① 解： 0 2 1 3 x y -1 0 3 1 x y 方程①所对应的直线是通过A（0， 1）和B（2，3）两点的直线 1l 方程②所对应的直线是通过C（－1，3） 和D（0，1）两点的直线 2l 由图可知，1l 2l与 交于（0，1） 所以，原方程组的解是      1 0 y x 11  yxl： 122  yxl ： 交点（0，1） 方程 ① 可化为 1 xy 方程② 可转化为 12  xy 通过以上探讨我们知道，用图象法解二元 一次方程组时，应先在同一平面直角坐标系内 画出相应的函数图象，这两条直线若相交，其 交点的坐标，就是方程组的解. 你能归纳运用图象法解二元一次方程组的 一般步骤吗？ 一般步骤 ①方程化成函数 ②画出函数图象 ③找出图象的交点坐标 ④写出方程组的解 1.利用函数图象：求出方程组      pnymx cbyax ① ② 的解. 答：此方程组的解是      1 2 y x -1 2 2.用图象法解下列二元一次方程组：      1 5 yx yx 解： 画出x+y=5的所对应的直线 画出x-y=1的所对应的直线 如图两条直线的交点坐 标是（3，2） 所以此方程组 的解是：      2 3 y x x+y=5 x-y=1 3 例2 利用图象法解方程组 5x-2y=4 10x-4y=8 解 对于方程①，有 3-2y 20x 过(0, -2)和(2, 3)画出 表示方程①的直线 同样，(0, -2)和(2, 3) 也在表示方程②的 直线上，所以方程 ①、 ②对应的直线 是通过(0, -2)和(2, 3) 两点的直线l，就是 说，这两条直线重 合，显然，直线l上 每一个点的坐标都 是原方程组的解， 所以原方程组有无 穷多组解 y 1 2 3 4 o 4321-1-2-3-4 x -1 -2 -3 -4 l：5x-2y=4 (10x-4y=8) 例3 利用图象法解方程组 3x+2y=-2 6x+4y=4 方程组中两个方程的所 对应的直线有怎样的位 置关系？方程组的情况 怎样？ 解：作出这两条直线 1 2 3 4 5 6 7 o 4321-1-2-3-4 x -1 -2 -3 -4 -5 8 3x+2y = -2 6x+4y = 4 如图，两条直线平行，所 以方程组无解 思考： • 以上几个方程组可以写成如下标准形式， 你能说出在什么情况下，方程有唯一的解， 在什么情况下方程有无数个解，在什么情 况下，方程无解吗？ a1x+b1y=c1 a2x+b2y=c2 x-y=-1 2x+y=1 5x-2y=4 10x-4y=8 3x+2y=-2 6x+4y=4 通过以上各例及练习，你能说说二元一次 方程组的解的情况吗？有什么样的规律吗？ 二元一次方程组 a1x+b1y=c1 a2x+b2y=c2 的解的情况有三种： 1.当 a1：a2 ≠b1：b2 时 ，方程组有唯一解； 2.当 a1：a2=b1：b2 =c1 :c2时，有无穷多解； 3.当a1：a2=b1：b2 ≠c1 :c2时，无解。 u通过以上学习你能发现二元一次方 程组的解有几种情况？ 二元一次方程组的解有以下三种情况 ①只有一组解（两直线只有一个交点） ②有无穷多组解（两直线重合） ③无解（两直线平行） Ø请问这节课你学到了那些知识和 数学方法？ Ø用图象法解方程组是数形结合的 一个典型应用. Ø用图象法解方程组的方法步骤你 会了吗？ Ø二元一次方程组的解有几种情况？ 课堂 小结