北师版八年下多边形及其角度计算 课后练习二及详解 4页

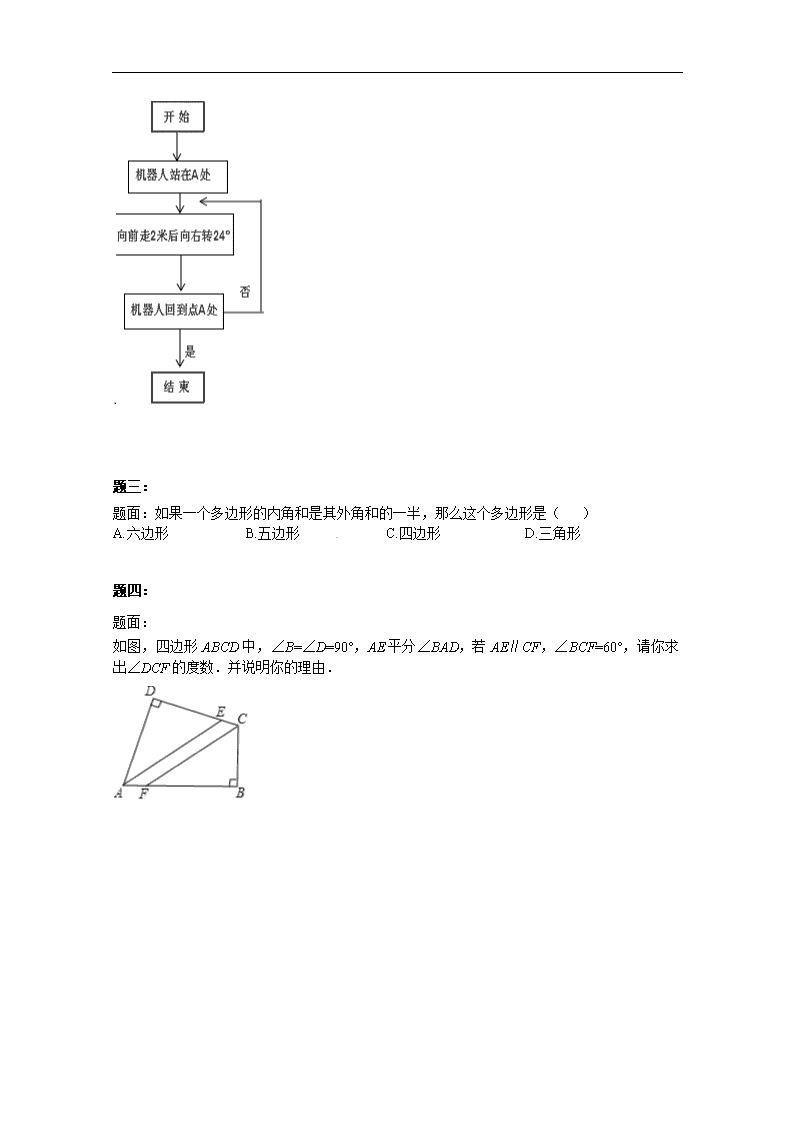
学科：数学 专题：多边形及其角度计算 主讲教师：傲德 [来源:www.shulihua.netwww.shulihua.net] 重难点易错点解析 题一： 题面：已知一个正多边形的一个内角是 120°，则这个多边形 的边数是 ． 金题精讲 题一： 题面：在下面四种正多边形的瓷砖中，用同一种瓷砖能镶嵌成一个平面图案的是（ ） A．①②③ B．①②④ C．①③④ D．②③④ 题二： 题面：有一程序，如果机器人在平地上按如图的步骤行走，那么机器人回到 A 点处共走的路 程是（ ） A．24 米 B．48 米 C．15 米 D．30 米 题三： 题面：如果一个多边形的内角和是其外角和的一半，那么这个多边形是（ ）[来源:www.shulihua.net] A.六边形 B.五边形 C.四边形 D.三角形 题四： 题面： 如图，四边形 ABCD 中，∠B=∠D=90°，AE 平分∠BAD，若 AE∥CF，∠BCF=60°，请你求 出∠DCF 的度数．并说明你的理由． [来源:www.shulihua.netwww.shulihua.net] 思维拓展 题面：四边形的四个内角中，最多有 个锐角，在四边形的四个外角中，最多有 ________________个锐角． 课后练习详解 重难点易错点解析 题一： 答案：六． 详解：外角是 180﹣120=60 度， 360÷60=6，则这个多边形是六边形． 故答案为：六． 金题精讲 题一： 答案：B. 详解：①正三角形的每个内角是 60°，能整除 360°，能密铺； ②正四边形的每个内角是 90°，4 个能密铺； ③正五边形的每个内角是 108°，不能整除 360°，不能密铺； ④正六边形的每个内角是 1 20°，能整除 360°，能密铺． 故同一种瓷砖能镶嵌成一个平面图案的是：①，②，④． 故选 B． 题二： 答案：D. 详解：利用多边形的外角和等于 360°，可知机器人回到 A 点时，恰好沿着 360°÷24°=15 边形 的边走了一圈，即可求得路程．2×(360°÷24°)=30 米．故本题选 D． 题三： 答案：D． 详解：任何多边形的外角和是 360 度，内角和等于外角和的一半则内角和是 180 度，可知此 多边形为三角形．根据题意，得 (n﹣2)•180°=180°，解得：n=3．故选 D． 题四： 答案：60°．[来源:www.shulihua.net] 详解：∠DCF=60°，理由如下： 如图，∵∠B =90° ∴∠1+∠BCF=90° ∵∠BCF=60° ∴∠1=30°． ∵AE∥CF ∴∠2=∠1=30° ∵AE 平分∠BAD ∴∠3=∠2=30° 又∵∠D=90° ∴∠3+∠4=90° ∴∠4=60° ∵AE∥CF ∴∠DCF=∠4=60°．[来源:www.shulihua.net] 思维拓展 答案： 3；3. 详解：根据四边形的内角和为 360°可知：一个四边形的四个内角中最多有 3 个钝角，最多有 3 个锐角． 在四边形的四个外角中，最多有 3 个锐角，最多有 3 个钝角． 故答案为：3，3．