八年级下数学课件：第十七章 勾股定理 复习（共27张PPT）_人教新课标 27页

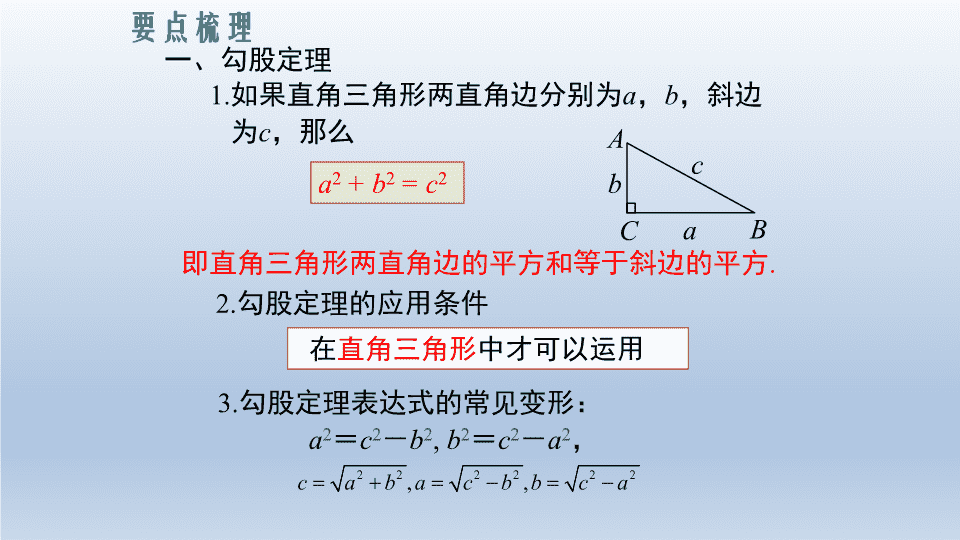
复习课件 第十七章 勾股定理 知识框架 勾股定理　 直角三角形边 长的数量关系　　 勾股定理 的逆定理　　 直角三角 形的判定　　 互逆定理 要点梳理 1.如果直角三角形两直角边分别为a，b，斜边 为c，那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方. 在直角三角形中才可以运用 2.勾股定理的应用条件 一、勾股定理 3.勾股定理表达式的常见变形： a2＝c2－b2, b2＝c2－a2， 2 2 2 2 2 2, ,c a b a c b b c a      A BC c a b 二、勾股定理的逆定理 1.勾股定理的逆定理 如果三角形的三边长a，b，c满足 a2 +b2=c2 ，那么这个三角形是直角三角形. 满足a2 +b2=c2的三个正整数，称为勾股数. 2.勾股数 3.原命题与逆命题 如果两个命题的题设、结论正好相反，那么把其中 一个叫做原命题，另一个叫做它的逆命题. A BC c a b 例1 在Rt△ABC中，∠ACB=90°，CD⊥AB于D， AC=20，BC=15. （1）求AB的长； （2）求BD的长． 解：（1）∵在Rt△ABC中，∠ACB=90°， （2）方法一：∵S△ABC= AC•BC= AB•CD， ∴20×15=25CD， ∴CD=12． ∴在Rt△BCD中， 2 2 2 220 15 25;AB AC BC      1 2 1 2 2 2 2 215 12 9.BD BC CD     考点一 勾股定理及其应用 考点讲练 方法二：设BD=x，则AD=25-x. 2 2 2 2 2 2, ,AC AD CD BC BD CD    2 2 2 2 ,AC AD BC BD     22 2 220 25 15 , 50 =450x x x     即 ， 解得x=9.∴BD=9. 方法总结 对于本题类似的模型，若已知两直角边求斜边上的 高常需结合面积的两种表示法起来考查，若是同本 题(2)中两直角三角形共一边的情况，还可利用勾 股定理列方程求解. 针对训练 1.Rt△ABC中，斜边BC=2，则AB2+AC2+BC2的值为 （　　） A.8 B.4 C.6 D.无法计算 A 3.一直角三角形的三边分别为2、3、x，那么以x为边 长的正方形的面积为___________. 2.如图，∠C=∠ABD=90°，AC=4，BC=3，BD=12， 则AD的长为______． 13或5 13 4．已知Rt△ABC中，∠C=90°，若a +b=14cm， c=10cm，求△ABC的面积. 解：∵a+b=14， ∴(a+b)2=196. 又∵a2+b2=c2=100， ∴2ab=196-(a2+b2)=96， ∴ ab=24．1 2 例2 我国古代数学著作《九章算术》中记载了一道有 趣的问题，这个问题的意思是：有一个水池，水面是 一个边长为10尺的正方形，在水池的中央有一根新生 的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸 边，它的顶端恰好到达岸边的水面，请问这个水池的 深度和这根芦苇的长度各是多少？ 解：如图，设水池的水深AC为x尺， 则这根芦苇长AD=AB=（x+1）尺， 在直角三角形ABC中，BC=5尺 由勾股定理得BC2+AC2=AB2, 即 52+ x2= (x+1)2 25+ x2= x2+2x+1， 2x=24， ∴ x=12， x+1=13. 答：水池的水深12尺，这根芦苇长13尺. D BC A 例3 如图所示，一只蚂蚁从实心长方体的顶点A出发， 沿长方体的表面爬到对角顶点C1处，问怎样走路线最 短？最短路线长为多少？ 解析：蚂蚁由A点沿长方体的表面 爬行到C1点，有三种方式： ①沿ABB1A1和A1 B1C1D1面；②沿ABB1A1和BCC1B1面； ③沿AA1D1D和A1B1C1D1面，把三种方式分别展成平 面图形如下： 解：在Rt△ABC1中， 2 2 2 2 2 1 1 4 3 25AC AB BC     ， 1 5.AC  在Rt△ACC1中， 2 2 2 2 2 1 1 6 1 37AC AC CC     ， 1 37.AC  在Rt△AB1C1中， 2 2 2 2 2 1 1 1 1 5 2 29AC AB B C     ， 1 29.AC  5 29 37 ＜ ＜ ， ∴沿路径走路径最短，最短路径长为5. 化折为直：长方体中求两点之间的最短距离，展开方 法有多种，一般沿最长棱展开，距离最短. 方法总结 针对训练 5.现有一长5米的梯子架靠在建筑物的墙上，它们 的底部在地面的水平距离是3米，则梯子可以到 达建筑物的高度是______米．4 在Rt△ABO中，OA＝2米，DC＝OB＝1.4米， ∴AB2＝22－1.42＝2.04. ∵4－2.6＝1.4，1.42＝1.96， 2.04＞1.96， 答：卡车可以通过，但要小心． 解：如图，过半圆直径的中点O，作直径的垂线交下 底边于点D，取点C，使CD＝1.4米，过C作OD的平 行线交半圆直径于B点，交半圆于A点. 6.如图，某住宅社区在相邻两楼之间修建一个上方 是一个半圆，下方是长方形的仿古通道，现有一辆 卡车装满家具后，高4米，宽2.8米，请问这辆送家 具的卡车能否通过这个通道？ 7.在O处的某海防哨所发现在它的北偏东60°方向相 距1000米的A处有一艘快艇正在向正南方向航行，经 过若干小时后快艇到达哨所东南方向的B处. （1）此时快艇航行了多少米(即AB 的长)？ 北 东 O A B 60° 45° C = 500 500 3AB AC BC   ( )米. 2 21000 500 500 3( ).OC    米 解：根据题意得∠AOC=30°， ∠COB=45°，AO=1000米. ∴AC=500米，BC=OC. 在Rt△AOC中，由勾股定理得 ∴BC=OC= 500 3 ,米 在O处的某海防哨所发现在它的北偏东60°方向相距 1000米的A处有一艘快艇正在向正南方向航行，经过 若干小时后快艇到达哨所东南方向的B处. （2）距离哨所多少米（即OB的长） ？ 北 东 O A B 60° 45° C    2 2 2 2 500 3 500 3 500 6( ). OB OC OB     米 解：在Rt△BOC中，由勾股定理得 例4 在△ABC中，AB=c，BC=a，AC=b， ， 2c-b=12，求△ABC的面积． 3 4 5 a b c  解：由题意可设a=3k，则b=4k，c=5k， ∵2c-b=12， ∴10k-4k=12， ∴k=2， ∴a=6，b=8，c=10， ∵62+82=102， ∴a2+b2=c2， ∴△ABC为直角三角形， ∴△ABC的面积为 ×6×8=24．1 2 考点二 勾股定理的逆定理及其应用 例5 B港有甲、乙两艘渔船，若甲船沿北偏东60°方 向以每小时8 n mile的速度前进，乙船沿南偏东某个 角度以每小时15 n mile的速度前进，2 h后，甲船到 M岛，乙船到P岛，两岛相距34 n mile，你知道乙船 是沿哪个方向航行的吗？ 解：甲船航行的距离为BM= 16（n mile）, 乙船航行的距离为BP= 30（n mile）． ∵162+302=1156，342=1156, ∴BM2+BP2=MP2, ∴△MBP为直角三角形，∴∠MBP=90° , ∴乙船是沿着南偏东30°方向航行的． 8.下列各组数中，是勾股数的为（　　） A．1，2，3 B．4，5，6 C．3，4，5 D．7，8，9 9.已知下列图形中的三角形的顶点都在正方形的 格点上，可以判定三角形是直角三角形的有 ________． 针对训练 (2)(4) C 10.如图，在四边形ABCD中，AB=20cm，BC=15cm， CD=7cm，AD=24cm，∠ABC=90°．猜想∠A与∠C 关系并加以证明． 解：猜想∠A+∠C=180°． 连接AC. ∵∠ABC=90°， ∴在Rt△ABC中，由勾股定理得 ∵AD2+DC2=625=252=AC2， ∴△ADC是直角三角形，且∠D=90°， ∵∠DAB+∠B+∠BCD+∠D=360°， ∴∠DAB+∠BCD=180°， 即∠A+∠C=180°． 2 2 2 2AC= 20 15AB BC = =25, 考点三 勾股定理与折叠问题 例6 如图，在长方形ABCD中，AB=3cm，AD=9cm， 将此长方形折叠，使点B与点D重合，折痕为EF，求 △ABE的面积. 解：∵长方形折叠，使点B与点D重合， ∴ED=BE. 设AE=xcm，则ED=BE=(9-x)cm， 在Rt△ABE中， AB2+AE2=BE2， ∴32+x2=(9-x)2， 解得x=4. ∴△ABE的面积为3×4× =6(cm2).1 2 方法总结 勾股定理可以直接解决直角三角形中已知两边求 第三边的问题；如果只知一边和另两边的关系时， 也可用勾股定理求出未知边，这时往往要列出方程 求解． 针对训练 11.如图，有一张直角三角形纸片， 两直角边AC＝6 cm，BC＝8 cm， 将△ABC折叠，使点B与点A重合， 折痕是DE，则CD的长 为 ． 1.75cm 考点四 本章解题思想方法 方程思想 例7 如图，在△ABC中，AB=17，BC=9，AC=10， AD⊥BC于D.试求△ABC的面积． 解：在Rt△ABD和Rt△ACD中， AB2-BD2=AD2，AC2-CD2=AD2， 设DC=x，则BD=9+x， 故172-(9+x)2=102-x2， 解得x=6. ∴AD2= AC2−CD2 = 64，∴AD=8. ∴S△ABC= ×9×8=36．1 2 解：当高AD在△ABC内部时，如图①. 在Rt△ABD中，由勾股定理， 得BD2＝AB2－AD2＝202－122＝162， ∴BD＝16. 在Rt△ACD中，由勾股定理， 得CD2＝AC2－AD2＝152－122＝81， ∴CD＝9.∴BC＝BD＋CD＝25， ∴△ABC的周长为25＋20＋15＝60. 例8 在△ABC中，AB＝20，AC＝15，AD为BC边上的高， 且AD＝12，求△ABC的周长． 分类讨论思想 题中未给出图形，作高构造直角三角形时，易漏掉钝 角三角形的情况．如在本例题中，易只考虑高AD在 △ABC内的情形，忽视高AD在△ABC外的情形． 当高AD在△ABC外部时，如图②. 同理可得 BD＝16，CD＝9. ∴BC＝BD－CD＝7， ∴△ABC的周长为7＋20＋15＝42. 综上所述，△ABC的周长为42或60. 方法总结 例9 有一圆柱体高为8cm，底面圆的半径为2cm，如 图.在AA1上的点Q处有一只蜘蛛，QA1=3cm，在BB1 上的点P处有一只苍蝇，PB=2cm．求蜘蛛爬行的最 短路径长(π取3). 解：如图，沿AA1剪开，过Q作QM⊥BB1于M，连接QP. 则PM=8-3-2=3(cm)， QM=A1B1= ×2×π×2=6(cm)， 在Rt△QMP中，由勾股定理得 答：蜘蛛爬行的最短路径长是 cm． 1 2 2 2 3 5cm.PQ QM PM   转化思想 3 5 谢 谢