2019八年级数学下册 第九章 中心对称图形—平行四边形小结与思考（1）导学案 5页

课题：第九章小结与思考（1）‎ 班级： 姓名： ‎ 一、学习目标 ‎1. 掌握图形的旋转、中心对称与中心对称图形的概念，并会作一个图形的旋转后的图形和关于一个点的对称图形 ‎2. 掌握平行四边形的性质与判定 ‎3. 进一步掌握综合法的证明格式以及分析的综合的思考方法 二、预习导航 ‎ ‎1.P90 阅读理解 三、课堂探究 ‎1.例题精讲 例1： 如图，在△ABC中，D是边AB的中点，E是AC上一点，EF∥AB，DF∥BE.‎ 试猜想DF与AE之间的关系，并说明你的猜想.‎ O 例2： 如图1，在□ABCD中，对角线AC、BD相交于点O，直线EF过点O与AB、CD分别相交于E、F.试探究OE与OF的大小关系并说明理由.‎ ‎ 图（1）‎ 变式训练 ‎ ‎1：在上述问题中，若直线EF绕点O旋转到与边DA、BC的延长线交于点E、F（如图2），上述结论是否仍然成立？试说明理由.‎ 5‎ ‎ 图（2）‎ ‎2：在上述问题中，若将直线EF绕点O旋转到如图（3）的位置，上述结论是否仍然成立？试说明理由.‎ ‎ 图（3）‎ 练一练 ‎1.已知：如图，在四边形ABCD中，AB∥CD，以AD，AC为邻边作□ACED，延长DC交EB于F，求证：EF＝FB.‎ 归纳小结：‎ 四、随堂演练 ‎【基础题】 ‎ ‎1. 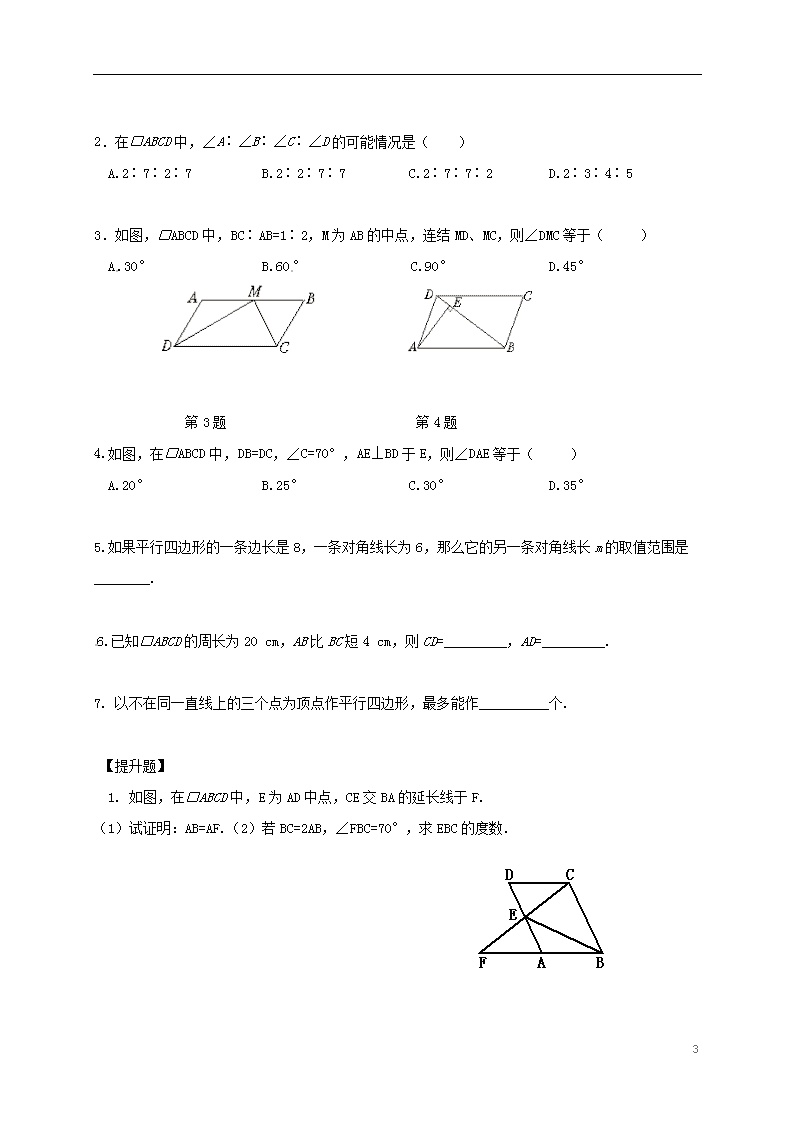下列几何图形中：（1）两条互相平分的线段；（2）两个互相交叉的圆；（3）两个有公共顶点的角；（4）有一个公共顶点的两个正方形.其中一定是中心对称图形的有 （   ）‎ A.1个 B.2个 C.3个 D.4个 5‎ ‎2．在□ABCD中，∠A∶∠B∶∠C∶∠D的可能情况是（ ）‎ A.2∶7∶2∶7 B.2∶2∶7∶‎7 C.2∶7∶7∶2 D.2∶3∶4∶5‎ ‎3．如图，□ABCD中，BC∶AB=1∶2，M为AB的中点，连结MD、MC，则∠DMC等于（ ）‎ A.30° B.60° C.90° D.45°‎ ‎ 第3题 第4题 ‎4.如图，在□ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE等于（ ）‎ A.20° B.25° C.30° D.35°‎ ‎5.如果平行四边形的一条边长是8，一条对角线长为6，那么它的另一条对角线长m的取值范围是________.‎ ‎6.已知□ABCD的周长为‎20 cm，AB比BC短‎4 cm，则CD=_________，AD=_________.‎ ‎7. 以不在同一直线上的三个点为顶点作平行四边形，最多能作__________个.‎ ‎ 【提升题】‎ ‎1. 如图，在□ABCD中，E为AD中点，CE交BA的延长线于F.‎ ‎（1）试证明：AB=AF.（2）若BC=2AB，∠FBC=70°，求EBC的度数.‎ 5‎ ‎【课后巩固】‎ ‎1. 用一副扑克牌做实验，选其中的黑桃5和方块4，是中心对称图形是 ( ) ‎ A.黑桃5 B.方块‎4 ‎ C.黑桃5和方块4 D.以上都不对 ‎2．判断一个四边形是平行四边形的条件是（ ）‎ A.一组对边相等，另一组对边平行 B. 一条对角线平分另一条对角线，且一组对边平行 C. 一组邻边相等，一组对边相等 D.一条对角线平分另一条对角线，且一组对边相等 ‎3. 如图，□ABCD中，GH过对角线的交点O，AB=5，AD=4，OH=2，则四边形BCGH的周长为（ ）‎ A.11 B‎.13 ‎ C.16 D.17‎ ‎ 第3题 第4题 第5题 第7题 ‎4. 如图，从等腰△ABC底边上任意一点D，作DE∥AC交AB于E，DF∥AB交AC于F，则□AEDF的周长（ ）‎ A.等于三角形周长 B.是三角形周长的一半 C.等于三角形腰长 D.是腰长的2倍 ‎5. 如图，若□ABCD的一内角∠BCD的平分线交AD于F，且CF=FD，则∠B的度数为_________.‎ ‎6. 延长△ABC的中线AD到E，使AE=2AD，则四边形ABEC是__________.‎ ‎7. 如图，E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件：___________，使四边形AECF是平行四边形.‎ ‎8. 如图，□ABCD的对角线AC、BD相交于点O，点E、F是OB、OD的中点，过点O任作一直线分别交AB、CD于点G、H. 求证：GF∥EH.‎ 5‎ ‎9. 如图，在□ABCD中，∠DAB=60°，点F、E分别在AB、CD的延长线上，且CF=BC，AE=AD.‎ ‎（1）四边形AFCE是平行四边形吗？说明理由.‎ ‎（2）若去掉已知条件的“∠DAB=60°”，上述结论还成立吗？成立，写出证明过程；不成立，说明理由.‎ 学后/教后思：‎ 5‎