- 1.04 MB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
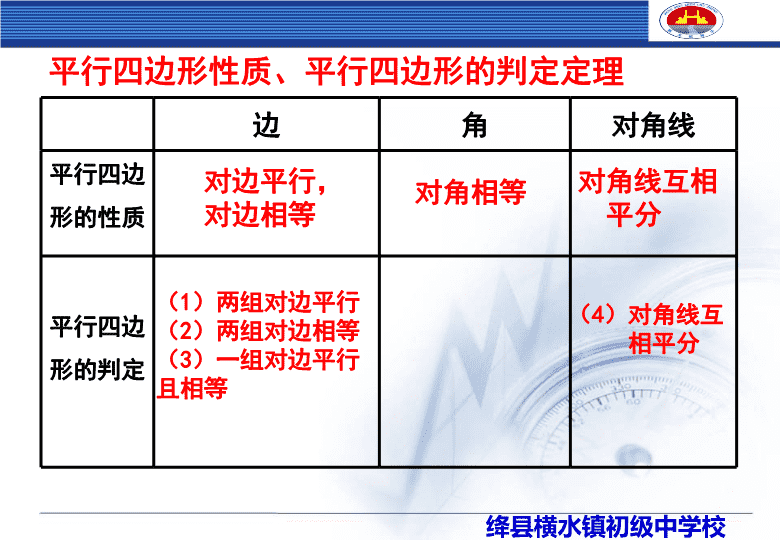
平行四边形性质、平行四边形的判定定理
边 角 对角线
平行四边
形的性质
平行四边
形的判定
对边平行,
对边相等 对角相等 对角线互相
平分
(1)两组对边平行
(2)两组对边相等
(3)一组对边平行
且相等
(4)对角线互
相平分
绛县横水镇初级中学校
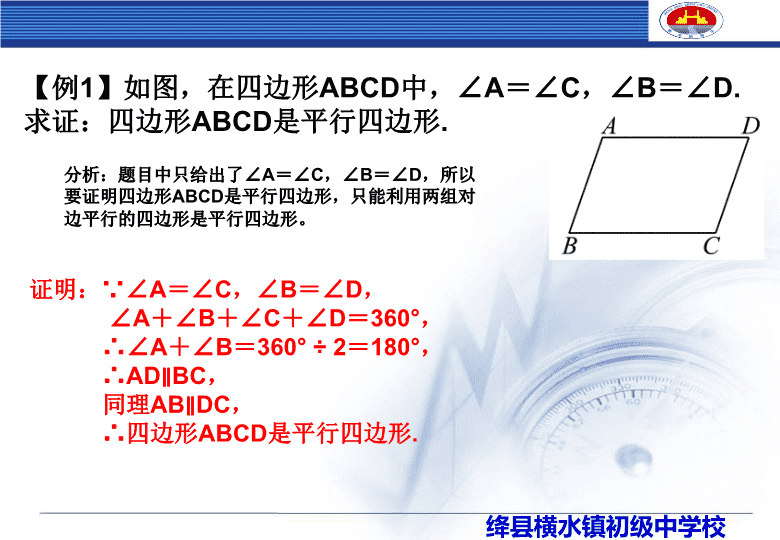
证明:∵∠A=∠C,∠B=∠D,
∠A+∠B+∠C+∠D=360°,
∴∠A+∠B=360° ÷ 2=180°,
∴AD∥BC,
同理AB∥DC,
∴四边形ABCD是平行四边形.
【例1】如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
绛县横水镇初级中学校
分析:题目中只给出了∠A=∠C,∠B=∠D,所以
要证明四边形ABCD是平行四边形,只能利用两组对
边平行的四边形是平行四边形。
【例2】如图,已知BD是△ABC的角平分
线,点E、F分别在边AB、BC上,
ED∥BC,EF∥AC.求证:BE=CF.
证明:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
∴EB=CF.
绛县横水镇初级中学校
【例3】如图所示,在平行四边形ABCD中,点E、F是对角
线AC上的两点,且AF=CE.求证:DE=BF.
解析:由已知想到连接DB,与AC相交于点O,
则有OD=OB,OE=OF;再利用判定定理4证明
四边形EBFD是平行四边形,进而结合平行四边
形的性质证明OE=OF.
证明:如图,连接BD,交AC于点O,连接DF、BE.
∵四边形ABCD是平行四边形,且点O为对角线的交点,
∴OD=OB,AO=CO.
又∵AF=EC,
∴AF-AO=CE-CO,
∴OF=OE,
∴四边形DEBF是平行四边形,
∴DE=BF.
绛县横水镇初级中学校
地址:山西省绛县横水镇
(外网)http://202.97.136.249:8001
(内网)http://172.30.0.30:8001
绛县横水镇初级中学校
相关文档
- 八年级下数学课件八年级下册数学课2021-11-0117页
- 八年级下数学课件八年级下册数学课2021-11-0120页
- 八年级下数学课件《二次根式的乘除2021-11-0112页
- 八年级下数学课件:19-1-1 变量与函2021-11-0123页
- 八年级下数学课件《统计的初步认识2021-11-019页
- 八年级下数学课件八年级下册数学课2021-11-0121页
- 八年级下数学课件《样本的可靠性》2021-11-0124页
- 八年级下数学课件2-1 多边形_湘教2021-11-0116页
- 八年级下数学课件《探索三角形相似2021-11-0111页
- 八年级下数学课件八年级下册数学课2021-11-0134页