2020年秋九年级数学上册 第3章 圆的基本性质 11页

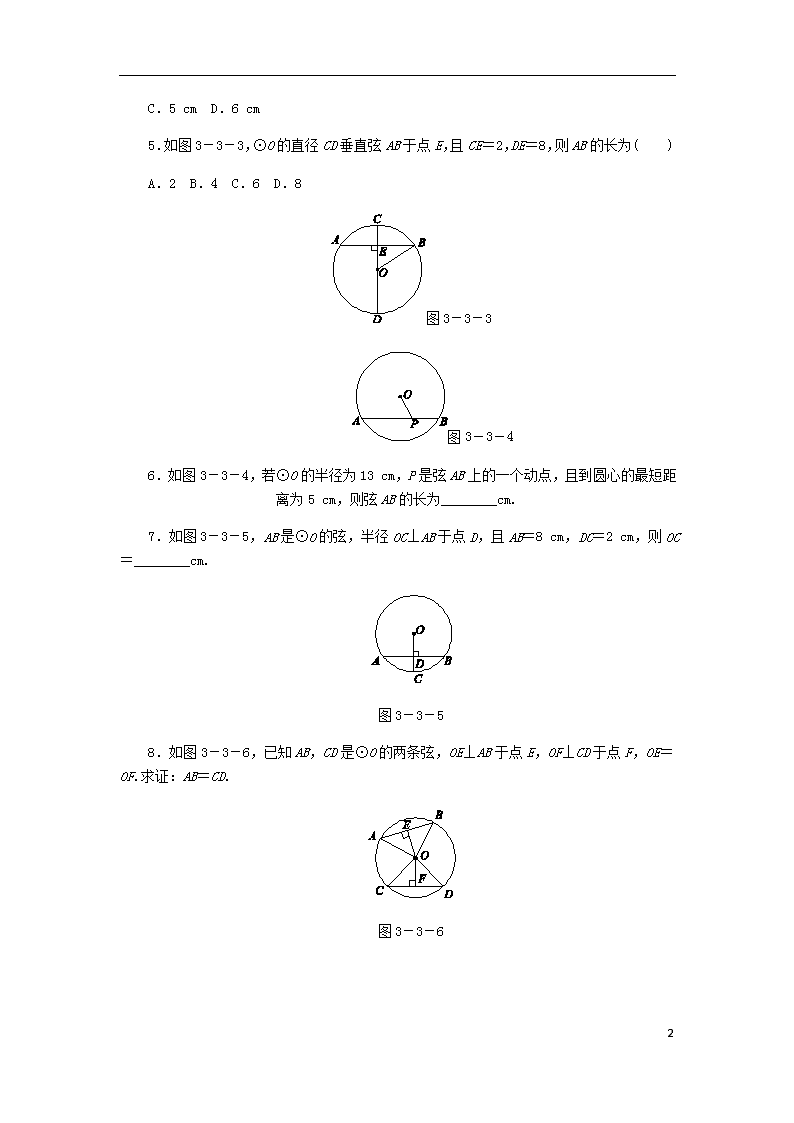
第3章　圆的基本性质 ‎3.3　垂径定理 第1课时　垂径定理 知识点1　圆的轴对称性 ‎1．圆的对称轴有(　　)‎ A．1条 B．2条 C．4条 D．无数条 ‎2．下列说法中，正确的是(　　)‎ A．直径是圆的对称轴 B．经过圆心的直线是圆的对称轴 C．与圆相交的直线是圆的对称轴 D．与半径垂直的直线是圆的对称轴 知识点2　垂径定理 ‎3．如图3－3－1，AB是⊙O的直径，弦CD⊥AB于点E，则CE＝________，＝________，＝________，△OCE≌________.‎ 图3－3－1‎ ‎　　　图3－3－2‎ ‎4．如图3－3－2，在半径为‎5 cm的⊙O中，弦AB＝‎6 cm，OC⊥AB于点C，则OC的长为(　　)‎ A．‎3 cm B．‎‎4 cm 11‎ C．‎5 cm D．‎‎6 cm ‎5．如图3－3－3，⊙O的直径CD垂直弦AB于点E，且CE＝2，DE＝8，则AB的长为(　　)‎ A．2 B．‎4 C．6 D．8‎ 图3－3－3‎ ‎　　　图3－3－4 ‎ ‎6．如图3－3－4，若⊙O的半径为‎13 cm，P是弦AB上的一个动点，且到圆心的最短距离为‎5 cm，则弦AB的长为________cm.‎ ‎7．如图3－3－5，AB是⊙O的弦，半径OC⊥AB于点D，且AB＝‎8 cm，DC＝‎2 cm，则OC＝________cm.‎ 图3－3－5‎ ‎8．如图3－3－6，已知AB，CD是⊙O的两条弦，OE⊥AB于点E，OF⊥CD于点F，OE＝OF.求证：AB＝CD.‎ 图3－3－6‎ 11‎ 知识点3　垂径定理在实际生活中的应用 ‎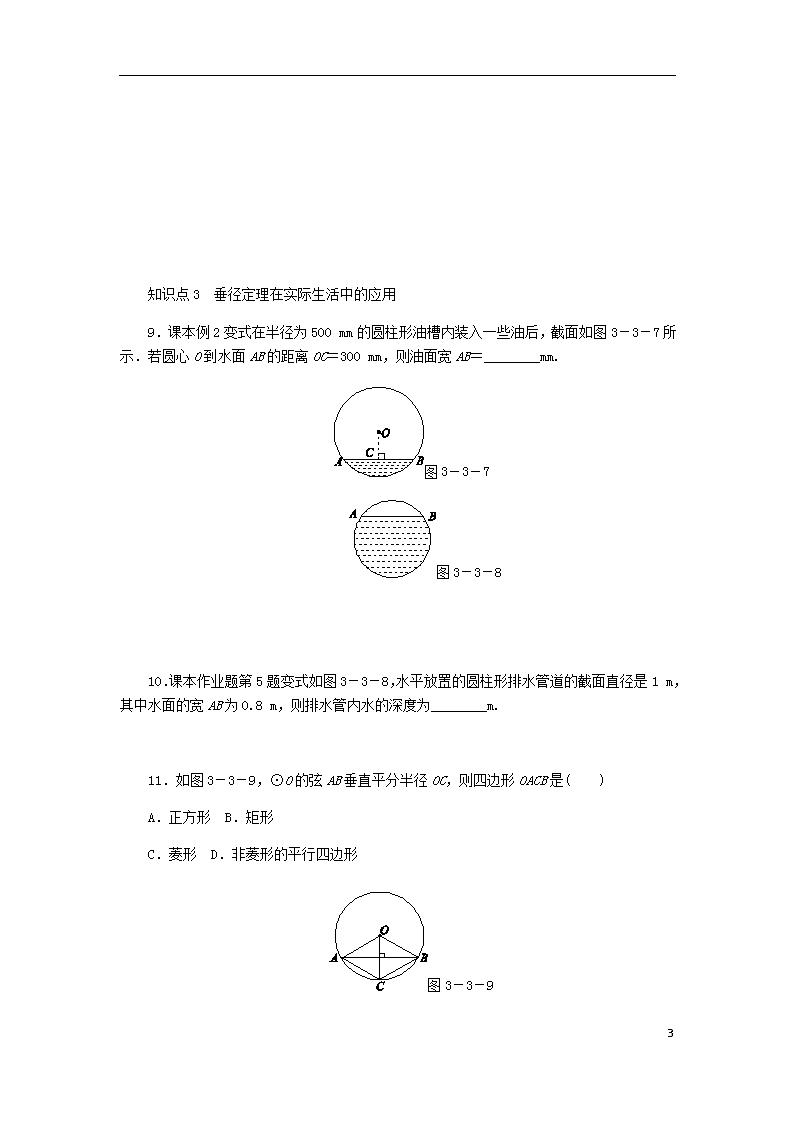9．课本例2变式在半径为‎500 mm的圆柱形油槽内装入一些油后，截面如图3－3－7所示．若圆心O到水面AB的距离OC＝‎300 mm，则油面宽AB＝________mm.‎ 图3－3－7‎ ‎　　图3－3－8‎ ‎10．课本作业题第5题变式如图3－3－8，水平放置的圆柱形排水管道的截面直径是‎1 m，其中水面的宽AB为‎0.8 m，则排水管内水的深度为________m.‎ ‎11．如图3－3－9，⊙O的弦AB垂直平分半径OC，则四边形OACB是(　　)‎ A．正方形 B．矩形 C．菱形 D．非菱形的平行四边形 图3－3－9‎ 11‎ ‎　　　图3－3－10‎ ‎12．如图3－3－10所示，AB，AC为⊙O中互相垂直的两条弦，且AB＝AC，OM⊥AB，ON⊥AC，垂足分别为M，N，OM＝3，则⊙O的半径为(　　)‎ A．3 B．‎2 C．3 D．2 图3－3－11‎ ‎13．2017·杭州模拟如图3－3－11，AB是⊙O的弦，C是AB上一点，∠AOC＝90°，OA＝8，OC＝6，则AB＝________．‎ ‎14．2016·杭州大江东期中在直径为20的⊙O中，弦AB，CD相互平行．若AB＝16，CD＝10，则弦AB，CD之间的距离是________．‎ ‎15．如图3－3－12，在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D.‎ ‎(1)求证：AC＝BD；‎ ‎(2)若大圆的半径R＝10，小圆的半径r＝8，且圆心O到直线AB的距离为6，求AC的长．‎ 图3－3－12‎ ‎16．如图3－3－13是一个半圆形桥洞的截面示意图，圆心为O，直径AB是河底线，弦CD 11‎ 是水位线，CD∥AB，且AB＝‎26 m，OE⊥CD于点E.水位正常时测得OE∶CD＝5∶24.‎ ‎(1)求CD的长；‎ ‎(2)现汛期来临，水面要以每小时‎4 m的速度上升，则经过多长时间桥洞会刚刚被灌满？‎ 图3－3－13‎ ‎17．如图3－3－14，在半径为5的扇形OAB中，∠AOB＝90°，C是上的一个动点(不与点A，B重合)，OD⊥BC，OE⊥AC，垂足分别为D，E.‎ ‎(1)当BC＝6时，求线段OD的长．‎ ‎(2)在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．‎ 图3－3－14‎ 11‎ 11‎ 详解详析 ‎1．D　2.B ‎3．DE　　　△ODE ‎4．B　[解析] 如图，连结OA.‎ ‎∵AB＝6 cm，OC⊥AB于点C，‎ ‎∴AC＝AB＝×6＝3(cm)．‎ ‎∵⊙O的半径为5 cm，‎ ‎∴OC＝＝＝4(cm)．‎ 故选B.‎ ‎5．D　[解析] ∵CE＝2，DE＝8，∴CD＝2＋8＝10，∴⊙O的半径为5，∴OE＝OC－CE＝5－2＝3.∵CD⊥AB，∴AE＝BE，∠OEB＝90°.在Rt△OEB中，OB＝5，OE＝3，根据勾股定理，得BE＝＝＝4，∴AB＝4＋4＝8.故选D.‎ ‎6．24‎ ‎7．5　[解析] 连结OA，因为半径OC⊥AB于点D，所以AD＝AB＝×8＝4(cm)．设⊙O的半径为x cm，在Rt△OAD中，OA2＝OD2＋AD2，即x2＝(x－2)2＋42，解得x＝5，所以OC＝‎5 cm.‎ ‎8．证明：∵OE⊥AB，OF⊥CD，‎ ‎∴AE＝BE，CF＝DF.‎ 在Rt△OBE与Rt△ODF中， ‎∴Rt△OBE≌Rt△ODF，‎ ‎∴BE＝DF，∴2BE＝2DF，即AB＝CD.‎ 11‎ ‎9．800‎ ‎10．0.8　[解析] 如图，过点O作OC⊥AB，C为垂足，直线OC交⊙O于点D，E，连结OA，则OA＝‎0.5 m.‎ ‎∵OC⊥AB，‎ ‎∴AC＝BC＝AB＝0.4 m.‎ 在Rt△AOC中，OA2＝AC2＋OC2，‎ ‎∴OC＝0.3 m，‎ ‎∴CE＝0.3＋0.5＝0.8(m)．‎ 即排水管内水的深度为0.8 m.‎ ‎11C‎　[解析] 由垂径定理知，OC垂直平分AB，即OC与AB互相垂直平分，所以四边形OACB是菱形．‎ ‎12．A　[解析] 要求圆的半径，连结OA，构造直角三角形OMA，已知OM＝3，故只需求出AM的长即可．由题意可得四边形OMAN为正方形，故AM＝OM＝3，所以OA＝3 .‎ ‎13．12.8　[解析] 如图，过点O作OD⊥AB，可得AD＝BD.‎ 在Rt△AOC中，OA＝8，‎ OC＝6，‎ 根据勾股定理得AC＝10.‎ ‎∵S△AOC＝OA•OC＝AC•OD，‎ 11‎ ‎∴OD＝4.8.‎ 在Rt△AOD中，根据勾股定理，得 AD＝＝6.4，‎ 则AB＝2AD＝12.8.‎ ‎14．[全品导学号：70392103]5 ±6‎ ‎[解析] 过点O作OE⊥AB于点E，交CD于点F，连结OA，OC，如图，‎ ‎∵AB∥CD，‎ ‎∴OF⊥CD，‎ ‎∴AE＝BE＝AB＝8，CF＝DF＝CD＝5.‎ 在Rt△AOE中，OE＝＝6.‎ 在Rt△OCF中，OF＝＝5 .‎ 当点O在AB和CD之间时，EF＝OE＋OF＝5 ＋6；‎ 当点O在AB，CD同一侧时，EF＝OF－OE＝5 －6.‎ ‎∴弦AB，CD之间的距离为5 ±6.‎ ‎15．解：(1)证明：如图，过点O作OE⊥AB于点E，则CE＝DE，AE＝BE，‎ ‎∴AE－CE＝BE－DE，‎ 即AC＝BD.‎ ‎(2)如图，连结OC，OA.‎ 由(1)可知，OE⊥AB且OE⊥CD，‎ 11‎ ‎∴CE＝＝＝2 ，‎ AE＝＝＝8，‎ ‎∴AC＝AE－CE＝8－2 .‎ ‎16．解：(1)如图，连结OD，‎ ‎∵直径AB＝26 m，‎ ‎∴OD＝AB＝×26＝13(m)．‎ ‎∵OE⊥CD，∴DE＝CD.‎ ‎∵OE∶CD＝5∶24，∴OE∶DE＝5∶12，‎ 设OE＝5x，DE＝12x，‎ ‎∵在Rt△ODE中，OE2＋DE2＝OD2，‎ ‎∴(5x)2＋(12x)2＝132，‎ 解得x＝1，‎ ‎∴CD＝2DE＝2×12×1＝24(m)．‎ ‎(2)由(1)得OE＝1×5＝5(m)．‎ 如图，延长OE交⊙O于点F，‎ 则EF＝OF－OE＝13－5＝8(m)．‎ ‎∵＝2(时)，‎ ‎∴经过2小时桥洞会刚刚被灌满．‎ ‎17．[全品导学号：70392107]解：(1)∵OD⊥BC，‎ ‎∴BD＝BC＝×6＝3.‎ 11‎ ‎∵∠BDO＝90°，OB＝5，BD＝3，‎ ‎∴OD＝＝4，‎ 即线段OD的长为4.‎ ‎(2)存在，DE的长保持不变．如图，连结AB.‎ ‎∵∠AOB＝90°，OA＝OB＝5，‎ ‎∴AB＝＝5 .‎ ‎∵OD⊥BC，OE⊥AC，‎ ‎∴D，E分别是线段BC，AC的中点，‎ ‎∴DE是△ABC的中位线，‎ ‎∴DE＝AB＝，‎ ‎∴DE的长保持不变，DE＝.‎ 11‎