江西专版2020中考数学复习方案第二单元方程组与不等式组第07课时不等式组的解法及不等式的应用课件 29页

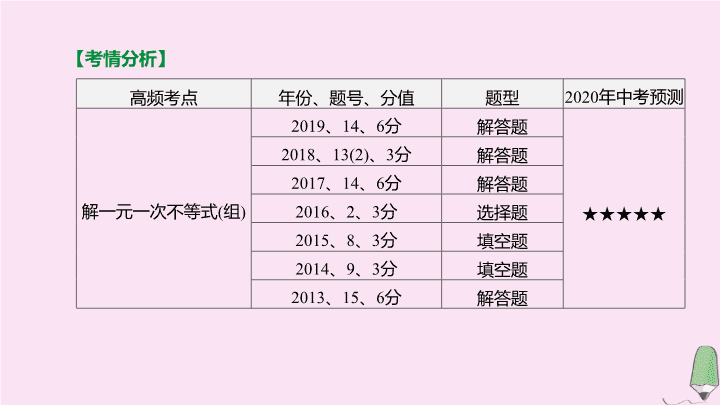
第 7 课时 不等式 ( 组 ) 的解法及不等式的应用 第二单元　方程 ( 组 ) 与不等式 ( 组 ) 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 解一元一 次不等式 ( 组 ) 2019 、 14 、 6 分 解答题 ★★★★★ 2018 、 13(2) 、 3 分 解答题 2017 、 14 、 6 分 解答题 2016 、 2 、 3 分 选择题 2015 、 8 、 3 分 填空题 2014 、 9 、 3 分 填空题 2013 、 15 、 6 分 解答题 5 . 一元一次不等式 : 含有一个未知数 , 未知数的次数是 ① 　　　　 的不等式 , 叫做一元一次不等式 .  1 . 不等式 : 用符号 “ < ”“ > ” 表示大小关系的式子 , 以及用 “≠” 表示不等关系的式子 , 叫做不等式 . 考点一　不等式的有关概念 1 考点聚焦 2 . 不等式的解 : 使不等式成立的未知数的值 . 3 . 不等式的解集 : 一个含有未知数的不等式的所有的解 , 组成这个不等式的解集 . 4 . 不等式组的解集 : 不等式组中所有不等式的解集的公共部分 . 考点二　不等式的性质 > > > < < 考点三　一元一次不等式 ( 组 ) 的解法 1 . 解一元一次不等式的一般步骤 : (1) 去分母 ;(2) 去括号 ;(3) 移项 ;(4) 合并同类项 ;(5) 系数化为 1 . 2 . 解一元一次不等式组的一般步骤 : (1) 解每个一元一次不等式 ; (2) 确定各不等式解集的公共部分 ; (3) 写出一元一次不等式组的解集 . x>b x ≤ a a ≤ x 小于 , 少于 , 不足 , 低于 < 至少 , 不低于 , 不小于 , 不少于 ≥ 至多 , 不超过 , 不高于 , 不大于 ≤ 题组一　必会题 对点演练 D B 2 . 某个关于 x 的一元一次不等式组的解集在数轴上的表示如图 7-2, 则该解集是 ( 　　 ) 图 7-2 A . -2 ” 还是 “≥” . A B 图 7-3 [ 答案 ] A 　 8 . 某校计划购买篮球和足球共 50 个 , 购买资金不超过 3000 元 . 若每个篮球 80 元 , 每个足球 50 元 , 则篮球最多可购买 ( 　　 ) A . 16 个 B . 17 个 C . 33 个 D . 34 个 考向一　解一元一次不等式 解 : x -5+2 > 2 x -6, x -2 x> -6+5-2, - x> -3, x< 3 . 所以原不等式的解集是 x< 3, 在数轴上表示如下 : 【 方法点析 】 解一元一次不等式的一般步骤 : 去分母、去括号、移项、合并同类项、系数化为 1 . 值得注意的是 , 去分母、系数化为 1 时 , 如果两边同乘负数 , 不等号一定要改变方向 ; 用数轴表示不等式的解集时 , 包含临界点时需用实心圆点 , 不包含临界点时需用空心圆圈 . | 考向精练 | 图 7-4 D 解 : 去分母 , 得 2( x -1)≥ x -2+6, 去括号 , 得 2 x -2≥ x -2+6, 移项 , 得 2 x - x ≥2-2+6, 合并同类项 , 得 x ≥6 . 考向二　解一元一次不等式组 | 考向精练 | -3