九年级数学上册第四章图形的相似阶段复习习题课件新版北师大版 44页

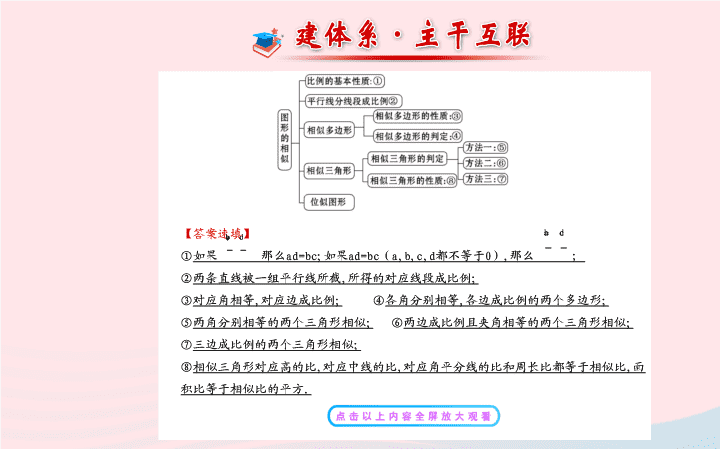
阶段复习课 第 四 章 主题 1 相似三角形 【 主题训练 1】 (2013 · 菏泽中考 ) 如图所示 , 在△ ABC 中 ,BC=6, E,F 分别是 AB,AC 的中点 , 动点 P 在射线 EF 上 ,BP 交 CE 于 D,∠CBP 的平分线交 CE 于 Q, 当 CQ= CE 时 ,EP+BP= 　　　　 . 【 自主解答 】 如图 , 当 CQ= CE 时 , 延长 BQ 交射线 EF 于点 G. ∵BQ 平分∠ CBP,∴∠CBQ=∠QBP, ∵E,F 是 AB,AC 的中点 , ∴EF∥BC,∴∠CBQ=∠QGP, ∴∠QBP=∠QGP,∴PB=PG. ∴EP+BP=EP+PG=EG. ∵EF∥BC,∴△BCQ∽△GEQ,∴ ∵CQ= CE, ∴ ∴EG=2BC,∵BC=6,∴EG=2×6=12. 答案 : 12 【 主题升华 】 1. 相似三角形的性质 (1) 对应角相等 , 对应边成比例 . (2) 对应高、中线、角平分线的比都等于相似比 . (3) 周长的比等于相似比 . (4) 面积之比等于相似比的平方 . 2. 相似三角形的判定 (1) 两个对应角相等的两个三角形相似 . (2) 两边对应成比例且夹角相等的两个三角形相似 . (3) 三边对应成比例的两个三角形相似 . 1.(2013 · 重庆中考 ) 如图 , 在平行四边形 ABCD 中 , 点 E 在 AD 上 , 连接 CE 并延长与 BA 的 延长线交于点 F, 若 AE=2ED,CD=3cm, 则 AF 的长为　 ( 　　 ) A.5 cm B.6 cm C.7 cm D.8 cm 【 解析 】 选 B.∵ 四边形 ABCD 是平行四边形 , ∴AB∥CD,∴∠F=∠ECD,∠FAE=∠CDE, ∴△AFE∽△DCE,∴ ∵AE=2ED,CD=3,∴ 解得 AF=6. 【 变式训练 】 (2013 · 安顺中考 ) 如图 , 在 □ ABCD 中 , 点 E 在 DC 上 , 若 DE∶EC=1∶2, 则 BF∶BE= 　　　　　 . 【 解析 】 因为四边形 ABCD 是平行四边形 , 所以 AB∥CD, 所以△ ABF∽△CEF. 又 DE∶EC=1∶2, 所以 BF∶EF=AB∶CE=CD∶CE=3∶2, 所以 BF∶BE=BF∶(BF+EF)=3∶5. 答案 : 3∶5 2.(2013 · 长春中考 ) 如图 ,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3, BD=2, 则 CD 的长为　 ( 　　 ) C.2 D.3 【 解析 】 选 B.∵∠ABD=∠BDC=90°,∠A=∠CBD, ∴△ABD∽△BDC,∴ 3.(2013 · 自贡中考 ) 如图 , 在平行四边 形 ABCD 中 ,AB=6,AD=9, ∠BAD 的平分线 交 BC 于 E, 交 DC 的延长线于 F,BG⊥AE 于 G, BG=4 , 则△ EFC 的周长为　 ( 　　 ) A.11 B.10 C.9 D.8 【 解析 】 选 D.∵AE 平分∠ BAD, ∴∠BAE=∠DAE,∵AD∥BC, ∴∠AEB=∠DAE,∴∠BAE=∠AEB, ∴AB=BE=6,∴EC=9-6=3,∵BG⊥AE, ∴AG=GE,∵ 则 AE=4.∴△ABE 的周长为 16, ∵AB∥DF,∴△EAB∽△EFC,∴△EFC 的周长为 8. 4.(2013 · 聊城中考 ) 如图 , 点 D 是△ ABC 的边 BC 上任一点 , 已知 AB=4,AD=2,∠DAC=∠B. 若 △ ABD 的面积为 a, 则△ ACD 的面积为　 ( 　　 ) 【 解析 】 选 C.∵∠DAC=∠B,∠ACD=∠BCA, ∴△ACD∽△BCA,∴ 因此△ ACD 与△ BCA 的相似比是 , 即面积比是 , 设△ ACD 的面积为 S, 则△ ABC 的面积为 S+a, 因此 解得 S= a. 5.(2013 · 恩施中考 ) 如图 , 在平行四边形 ABCD 中 ,AC 与 BD 交于点 O,E 为 OD 的中点 , 连接 AE 并延长交 DC 于点 F, 则 DF∶FC= 　 ( 　　 ) A.1∶4 B.1∶3 C.2∶3 D.1∶2 【 解析 】 选 D.∵ 四边形 ABCD 是平行四边形 , ∴AB∥CD,AB=CD,DO=BO. ∵ E 为 OD 的中点 ,∴DE∶EB=1∶3. ∵AB∥CD,∴△DEF∽△BEA, ∴DF∶AB=DE∶EB=1∶3, ∴DF∶DC=1∶3, 即 DF∶FC=1∶2. 6.(2013 · 龙东中考 ) 如图所示 ,D,E 分别是△ ABC 的边 AB,AC 上的点 , 试添加一个条件 : 　　　　　　　　 , 使得△ ABC∽△AED. 【 解析 】 ∵∠A=∠A,∴ 当∠ AED=∠B 或∠ ADE=∠C 时 , 根据 “ 两角对应相等两三角形相似 ” 可使△ ABC∽△AED. ∵∠A=∠A,∴ 当 时 , 根据 “ 两边对应成比例并且夹角相等的两三角形相似 ” , 可使△ ABC∽△AED. 答案 : ∠AED=∠B( 或∠ ADE=∠C 或 答案不唯一 ) 【 知识归纳 】 相似三角形判定的两种方法 7.(2012 · 衢州中考 ) 如图 , ▱ ABCD 中 ,E 是 CD 的延长线上一点 ,BE 与 AD 交于点 F,CD=2DE. 若△ DEF 的面积为 a, 则 ▱ ABCD 的面积为 　　　　 ( 用 a 的代数式表示 ). 【 解析 】 ∵ 四边形 ABCD 是平行四边形 , ∴AB∥CD,AD∥BC,AB=CD. ∴△DEF∽△CEB,△DEF∽△ABF, ∴ ∵CD=2DE,∴DE∶CE=1∶3,DE∶AB=1∶2. ∵S △DEF =a,∴S △CBE =9a,S △ABF =4a. ∴S 四边形 BCDF =S △CEB -S △DEF =8a, ∴S ▱ ABCD =S 四边形 BCDF +S △ABF =8a+4a=12a. 答案 : 12a 8.(2013 · 眉山中考 ) 如图 ,△ABC 中 ,E,F 分别是 AB,AC 上的两点 , 且 若△ AEF 的面积为 2, 则四边形 EBCF 的面积为 　　　　 . 【 解析 】 ∵ ∠A=∠A, ∴△AEF∽△ABC,∴ ∵△AEF 的面积为 2,∴S △ABC =18. ∴S 四边形 EBCF =S △ABC -S △AEF =18-2=16. 答案 : 16 主题 2 相似三角形的应用 【 主题训练 2】 (2013 · 滨州中考 ) 某高中学校为高一新生设计的学生板凳的正面视图如图所示 . 其中 BA=CD,BC=20cm,BC,EF 平行于地面 AD 且到地面 AD 的距离分别为 40cm,8cm, 为使板凳两腿底端 A,D 之间的距离为 50cm, 那么横梁 EF 应截取多长 ?( 材质及其厚度等暂忽略不计 ) 【 自主解答 】 过点 C 作 CM∥AB, 分别交 EF,AD 于 N,M, 作 CP⊥AD, 分别交 EF,AD 于 Q,P. 由题意 , 得四边形 ABCM 是平行四边形 , ∴EN=AM=BC=20(cm), ∴MD=AD-AM=50-20=30(cm). 由题意知 CP=40cm,PQ=8cm,∴CQ=32cm. ∵EF∥AD,∴△CNF∽△CMD.∴ 即 解得 NF=24cm. ∴EF=EN+NF=20+24=44(cm). 答 : 横梁 EF 应为 44cm. 【 主题升华 】 相似三角形的应用 1. 相似三角形的相关知识在生活中有着广泛的应用 , 如测量高度、宽度等 . 2. 解答步骤为 : 首先把实际问题转化为数学模型 , 然后构造相似三角形 , 再依据相似三角形的对应线段成比例列式求解 . 【 知识拓展 】 常见的相似三角形模型如下 1.(2013 · 巴中中考 ) 如图 , 小明在打网球时 , 使球恰好能打过网 , 而且落在离网 4m 的位置上 , 则球拍击球的高度 h 为 　　　　　 . 【 解析 】 ∵DE∥BC,∴△ADE∽△ACB, 即 ∴ h=1.5. 答案 : 1.5m 2.(2013 · 牡丹江中考 ) 劳技课上小敏拿出了一个腰长为 8cm, 底边为 6cm 的等腰三角形 , 她想用这个等腰三角形加工成一个边长比是 1∶2 的平行四边形 , 平行四边形的一个内角恰好是这个等腰三角形的底角 , 平行四边形的其他顶点均在三角形的边上 , 则这个平行四边形的较短的边长为 　　　　　　 . 【 解析 】 如图 1, 在等腰三角形 ABC 中 ,AB=AC=8,BC=6, 四边形 BDEF 为平行四边形 , 且 BD∶BF=1∶2, 设 BD=x, 则 DE=BF=2x. ∵DE∥BC,∴△ADE∽△ABC,∴ 即 如图 2, 同理可得 这个平行四边形的较短的边长为 答案 : 3.(2012 · 青海中考 ) 如图 , 利用标杆 BE 测量建筑物的高度 , 标杆 BE 高 1.5m, 测得 AB=2m,BC=14m, 则楼高 CD 为 　　　　 m. 【 解析 】 ∵CD∥EB, ∴△ABE∽△ACD, ∴ ∵AB=2m,BC=14m,EB=1.5m, ∴CD=12m, 故楼高 CD 为 12m. 答案 : 12 主题 3 位似 【 主题训练 3】 (2013 · 南宁中考 ) 如图 , △ABC 三个顶点坐标分别为 A(-1,3), B(-1,1),C(-3,2). (1) 请画出△ ABC 关于 y 轴对称的△ A 1 B 1 C 1 . (2) 以原点 O 为位似中心 , 将△ A 1 B 1 C 1 放大 为原来的 2 倍 , 得到△ A 2 B 2 C 2 , 并求出 的值 . 【 自主解答 】 (1) 如图所示 : (2) 如 (1) 中图所示 ( 也可在第一象限将原三角形放大二倍 ) 方法一 : 方法二 :∵△A 1 B 1 C 1 ∽△A 2 B 2 C 2 .∴ 【 主题升华 】 位似的三种规律 1. 位似判断 : 相似是前提 , 对应点的连线都过同一点是保证 . 2. 作图原理 : 位似中心、对应点连线共线且两对应点与位似中心的距离之比等于位似比 . 3. 位似与坐标 : 在平面直角坐标系中 , 如果位似变换是以原点为位似中心 , 相似比为 k, 那么位似图形对应点的坐标的比等于 k 或 -k. 1.(2012 · 玉林中考 ) 如图 , 正方形 ABCD 的两 边 BC,AB 分别在平面直角坐标系的 x 轴、 y 轴 的正半轴上 , 正方形 A′B′C′D′ 与正方形 ABCD 是以 AC 的中点 O′ 为中心的位似图形 , 已知 AC=3 , 若点 A′ 的坐标为 (1,2), 则正方形 A′B′C′D′ 与正方形 ABCD 的相似比是　 ( 　　 ) 【 解析 】 选 B.∵ 在正方形 ABCD 中 ,AC=3 , ∴BC=AB=3, 延长 A′B′ 交 BC 于点 E, ∵ 点 A′ 的坐标为 (1,2), ∴OE=1,EC=3-1=2=A′E, ∴OE∶BC=1∶3,∴AA′∶AC=1∶3, ∵O′A=O′C,∴O′A′∶AO′=1∶3, ∴ 正方形 A′B′C′D′ 与正方形 ABCD 的相似比是 . 2.(2012 · 钦州中考 ) 图中两个四边形是位似图形 , 它们的位似中心是　 ( 　　 ) A. 点 M B. 点 N C. 点 O D. 点 P 【 解析 】 选 D. 点 P 在对应点 M 和点 N 所在直线上 , 再利用连接另两个对应点 , 得出相交于 P 点 , 即可得出 P 为两图形位似中心 .