中考数学专题复习练习：二次根式教材分析 13页

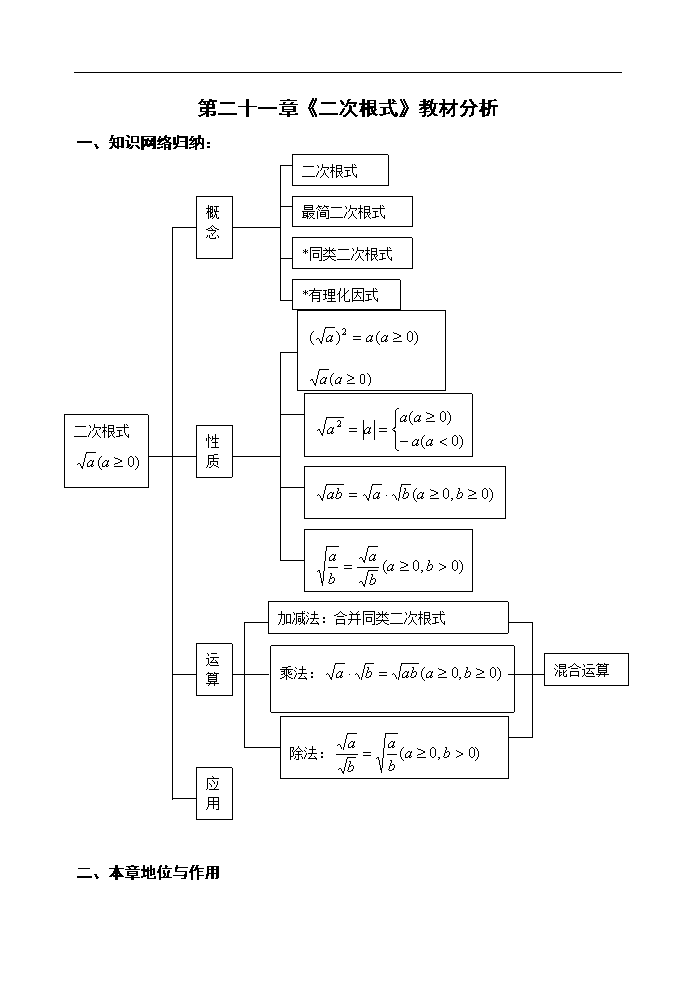
‎ ‎ 第二十一章《二次根式》教材分析 ‎ 二次根式 一、知识网络归纳：‎ 最简二次根式 概 念 ‎*同类二次根式 ‎*有理化因式 性 质 二次根式 加减法：合并同类二次根式 乘法：‎ 混合运算 运 算 除法：‎ 应用 二、本章地位与作用 ‎ ‎ 承上启下的作用，与前面学过的实数、整式两章有非常紧密的联系，二次根式的化简对勾股定理的应用是很好的补充；二次根式的概念、性质、化简与运算是后续学习解直角三角形、一元二次方程和二次函数的基础.‎ 三、中考考试要求及本章内容在近年中考中所占分值:‎ 基 本 要 求 略 高 要 求 二次根式及其性质 了解二次根式的概念，会确定二次根式有意义的条件 会利用二次根式的性质进行化简；能根据二次根式的性质对代数式做简单变形，在特定条件下确定字母的值 二次根式的 化简和运算 理解二次根式的加减乘除运算法则 会进行二次根式的化简，会进行二次根式的混合运算（不要求分母有理化）‎ 四、关注几个问题 ‎1．（1）教材中有代数式的概念，但没有同类二次根式的概念和分母有理化的概念； ‎ ‎(2)教材中去掉了对的化简；‎ ‎(3)教材中去掉了复杂的混合运算；‎ ‎(4)教材中没有二次根式比大小的问题.‎ ‎2．教学难度的降低 教材中删去了复杂的混合运算和的化简，从而降低了教学难度，将难点放在正确理解二次根式的性质和运算法则的合理性。‎ 五、教学建议 ‎（一）加强与实际的联系，突出二次根式的数学本质 例1．①在交通事故的处理中，交通警察往往用公式来判断该车是否超速，其中 表示车速（单位km/s）,表示刹车后车轮划过的距离（单位：）,表示摩擦系数；某日，在一段限速60km/s的公路上，发生了一起两车追尾的事故，警察赶到后，经过测量，得出其中一辆车的，，请问该车超速了吗？(,该车超速)‎ ‎ ‎ ‎ ②某人用一架不等臂天平称一块铁的质量，把铁块放在天平左盘时，称得它的质 量为300克；把铁块放在天平右盘时，称得它的质量为90 克，利用所学知识，求这块铁的实际质量.（约520克）‎ ‎ ③我们人体含有多少脂肪才算适当？据科学研究表明，可以利用身体的体重（，单位：千克）和身高（，单位：米）来计算身体脂耪水平，也称为身体质量指数（BMI）.计算公式是BMI=，而且男性的BMI指数范围是24~27，如果一位男生体重是70千克，身体脂肪属于正常，那么请你估计他的身高大约在哪个范围内？（精确到0.01米）（）‎ ‎ ④有一块如图所示的大理石板，请你把它切成三块，然后拼成一个 正方形的桌面.‎ ‎ ⑤如图，将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm ‎ 和10cm的长方体无盖盒子中，则细木棒露在盒外面的最短长 度是　　　　cm.‎ ‎ (二)加强知识间的纵向联系，充分理解概念与性质 ‎1．关于二次根式的概念，要注意以下几点：‎ ‎ （1）从形式上看，二次根式是以根号“”表示的代数式,这里的开方运算是最后一步运算.如等不是二次根式,而是含有二次根式的代数式或二次根式的运算;‎ ‎ （2）当一个二次根式前面乘有一个有理数或有理式（整式或分式）时，虽然最后运算不是开方而是乘法，但为了方便起见，我们把它看作一个整体仍叫做二次根式，而前面与其相乘的有理数或有理式就叫做二次根式的系数；‎ ‎ （3）二次根式的被开方数，可以是某个确定的非负实数，也可以是某个代数式表示的数，但其中所含字母的取值必须使得该代数式的值为非负实数；‎ ‎ （4）象“”等虽然可以进行开方运算，但它们仍属于二次根式。‎ ‎2．二次根式的主要性质：‎ ‎(1)； (2)； (3)；‎ ‎ ‎ ‎(4) 积的算术平方根的性质：；‎ ‎(5) 商的算术平方根的性质：；(6)若，则.‎ ‎3．注意与的逆用.‎ ‎4．注意本章知识与已学过知识的综合.‎ 例2．在实数范围内分解因式：‎ ‎ （1） （2） （3） ‎ o ‎（4） （5） (6)‎ 例3．右图是直线：（、是常数）的图象，‎ 化简：‎ 例4．如果把表示成，，表示成,‎ 求：的值.‎ ‎ 例5．如图，数轴上A、B两点表示的数分别为1和，点B关于点A的对称点为点C，则点C所表示的数是（ ）‎ A． B． C． D．‎ ‎ (三)注意对教材中的小贴士的处理:‎ ‎1. 最简二次根式的概念中,学生对于“开得尽方的因数或因式”不容易理解, 教材在 p.11及p.13两次出现同一个小贴士解释开得尽方的因数或因式:可以开方后移到根 号外的因数或因式.‎ ‎ 2. 小贴士中有对于运算结果有明确的规定:教材p.13: “在二次根式的运算中,最后结果一般要求分母中不含二次根式”.‎ ‎3. 对于二次根式的运算, 教材利用小贴士类比了它与实数、整式运算的联系:‎ ‎ ‎ ‎ 教材p.17: “在有理数范围内成立的运算律,在实数范围内仍成立”;‎ ‎ 教材p.20: “在二次根式的运算中,多项式乘法法则和乘法公式仍然适用”. ‎ ‎(四)加强运算能力，培养学生的观察能力、灵活的运算能力及估算能力 ‎1．二次根式的乘除运算:二次根式相乘除,把被开方数相乘除,根指数不变.‎ ‎(1)加大学生的探索空间，由特殊到一般，理解二次根式乘除运算法则的合理性；‎ ‎ (2)根据教学内容逐步明确运算结果的要求,不断归纳运算结果应满足的两个要求：‎ ‎ ①应为最简二次根式(包括两个条件)或有理式；‎ ‎ ②分母中不含根号.‎ ‎(3)注意让学生知道每一步运算的算理；‎ ‎(4)注意公式的推广： ‎ ‎ .‎ ‎2．二次根式的加减运算:先将二次根式化为最简二次根式,再将被开方数相同的二次根式 ‎ ‎ 进行合并.‎ ‎(1)用实例引入，体现研究二次根式 ‎ (2)可补充同类二次根式的概念.‎ ‎ (3)二次根式的加减运算需要先化为最简二次根式，再类比整式加减运算中的合并同类 ‎ 项，明确二次根式加减运算的实质是合并同类二次根式.‎ ‎3．二次根式的混合运算 ‎(1) 明确整式的运算顺序、运算法则、公式和运算律在二次根式的运算中同样适用, 教学中要注意本章内容与“整式”中相关内容的联系，使学生的学习形成正迁移.在讲述实例时与整式的相关运算类比:‎ 例6．先将化简，然后自选一个合适的值代入求值.‎ 例7．如果，那么=_____.‎ 例8．(08，宁波)若实数满足，则的值是 .‎ ‎(2)控制运算的难度.‎ ‎ ‎ ‎4. 掌控学生易错的环节，及时分析错因，不断巩固提高.‎ ‎ 例．下列根式化简是否正确？如果不正确，请你把正确的答案写下来：‎ ‎ （1） （2）‎ ‎ （3） （4）‎ ‎※5．分母有理化:将分母中的根号化去,分数值不变,叫做分母有理化.‎ ‎(1)常用的二次根式的有理化因式：‎ ‎ ①与互为有理化因式;‎ ‎ ②与、与互为有理化因式;‎ ‎ ③与、与互为有理化因式.‎ ‎(2) 在进行分母有理化时，应先将二次根式尽量化简；在找有理化因式时，找分母最简有理化因式；计算或化简的结果应化为最简形式。‎ ‎6．教会学生运算的技巧.‎ ‎ 例9. 计算：① ; ② ;‎ ‎ ③ .‎ ‎ 例10. 化简：‎ ‎ 例11．化简 ‎7．精讲多练，为后续学习打基础，二次根式的加、减、乘、除运算是后续学习解直角三角形、一元二次方程和二次函数的重要基础。‎ ‎（五）重视二次根式的化简 ‎1．二次根式的化简是本章的主要内容之一，掌握化简的方法需要进行一定的训练；‎ ‎ ‎ ‎2. 二次根式的化简求值问题, 要考虑字母取值的化简, 二次根式的化简, 二次根式的 ‎ ‎ 适当变形, 整体代入等多方面因素, 要先观察算式,选择合适的方法使运算简化.‎ ‎ 例12. ①已知: , , 求x2 - xy + y2 的值 ‎ ②已知: , 求: (1) 的值; (2) 的值 ‎ ③已知: x + y = -3, xy = 2, 求的值 ‎ ④已知 , 求的值. ‎ ‎ ⑤已知++= , 求x、y、z的值.‎ ‎ ⑥已知x＝ , y＝ , 求的值. ‎ ‎ ⑦已知 , 求的值. ‎ ‎（六）适当补充二次根式比大小的内容：‎ ‎1. 引导学生总结常用的比较大小的方法 ‎ 两个实数a,b比较大小，一般有“比”与“较”两种方法：‎ ‎①将两个实数相除（比）：若，当b>0时，则a>b；当b<0时，则a0时，则ab.‎ ‎②将两个实数相减（较）：若a-b>0，则a>b；‎ ‎ 若a-b=0，则a=b；‎ ‎ 若a-b<0，则a0，b>0）‎ ‎（七）思想方法总结 ‎(1)“特殊到一般”与“一般到特殊”； (2)类比思想； (3)转化思想.‎ 七、相关练习：‎ ‎（一）．二次根式的概念和性质 ‎1. 下列各式中，哪些是二次根式？哪些不是二次根式？为什么？‎ ‎ ‎ ‎ ‎ ‎2．x是怎样的实数时，下列各式在实数范围内有意义？‎ ‎ (1) ; (2); (3) ; (4)； (5);‎ ‎ (6)； （7）－ （8）－； （9）．‎ ‎3. 当时，.‎ ‎ ‎ ‎4. 在、、、、、中，最简二次根式有_______.‎ ‎5. 在实数范围内分解因式：=_____________；‎ ‎*6.把根号外的因式移到根号内：=____________.()‎ ‎7．若x、y为实数，y＝＋＋3．求yx的值．‎ ‎8．已知＋＋＝0．求a、b、c的值．‎ ‎9．根据下列条件，求字母x的取值范围：‎ ‎（1）＝1－x； （2）＝1．‎ ‎10．已知为三角形的三边，则= ‎ ‎11．比较大小(1); (2)‎ ‎12.( 08，济宁)若，则的取值范围是 A． B． C． D．‎ ‎※13.已知a<0，化简二次根式的正确结果是（ ）‎ A． B． C． D．‎ ‎14．若最简二次根式与最简二次根式可以合并，则的取值为____.‎ ‎15．已知都为正整数，且，则的值为_______.‎ ‎（二）二次根式的运算 ‎1．计算：（1）． （2）＋(－1)3－2× ‎ (3)． (4)．‎ ‎ ‎ ‎ (5)． (6). ‎ ‎(7)． (8). ‎ ‎(9).－―＋（a＞0，b＞0） （10）‎ ‎※（11）. ※(12)． ‎ ‎2．计算：(1); (2); ‎ ‎ (3); (4); (5); ‎ ‎ (6) ; (7) ; (8)‎ ‎3．计算：(1) (2) ‎ ‎(3) (4) *(5)‎ ‎4．解方程（组）：① ② ‎ ‎5. 若的整数部分是a，小数部分是b，则 ‎ ‎6．在数轴上与表示的点的距离最近的整数点所表示的数是___________‎ ‎7．若一个正方体的长为，宽为，高为，则它的体积为 .‎ ‎ ‎ ‎※8．的关系是 ‎ ‎9．甲、乙两人对题目“化简并求值：，其中”有不同的解答，‎ 甲的解答：，乙的解答：‎ ‎,谁的解答是错了?为什么?‎ ‎※10. 先观察下列分母有理化：，‎ 从计算结果中找出规律，再利用这一规律计算下列式子的值：‎ ‎11. 观察下列各式的特点：‎ ‎，，，……‎ ‎(1)请根据以上规律填空 ‎ ‎(2)请根据以上规律写出第
个不等式，并证明你的结论.‎ ‎※(3)计算下列算式：‎ ‎（三）二次根式的化简求值 ‎1．若，求的值.‎ ‎2．若求的值.‎ ‎3．已知，求的值.‎ ‎ ‎ ‎4．已知，，求(1)的近似值； ‎ ‎(2)的近似值； (3) 的近似值.(精确到0.01)‎ ‎5．已知，，求的值.‎ ‎6．已知：，求(1)的值； *(2)的值.‎ ‎7．已知：，求的值.‎ ‎8．已知：，求的值.‎ ‎（四）二次根式的应用 ‎1．设等腰三角形的腰长为a，底边长为b，底边上的高为h．‎ ‎（1）如果a＝2，b＝，求h；A B C D E F G H J I （2）如果b＝，h＝2，求a．（）‎ ‎2．ABCD是边长为1的正方形，以对角线AC为边作第2个正 方形ACEF, 再以对角线AE为边作第3个正方形, 如此下去…‎ ‎（1）记正方形ABCD的边长a1=1，按上述方法所做的正方形 的边长依次为a2，a3，a4，…an请求出a2，a3，a4的长；‎ ‎（2）根据以上规律写出an表达式.‎ ‎3．先阅读下列的解答过程，然后作答：‎ 有这样一类题目：将化简，若你能找到两个数和，使且，则可变为，即变成开方，从而使得化简。‎ 例如： ==，‎ ‎ ‎ ‎∴‎ 请仿照上例解下列问题：（1）； （2）‎