初中数学中考总复习课件PPT：第11课时　一次函数及其应用 43页

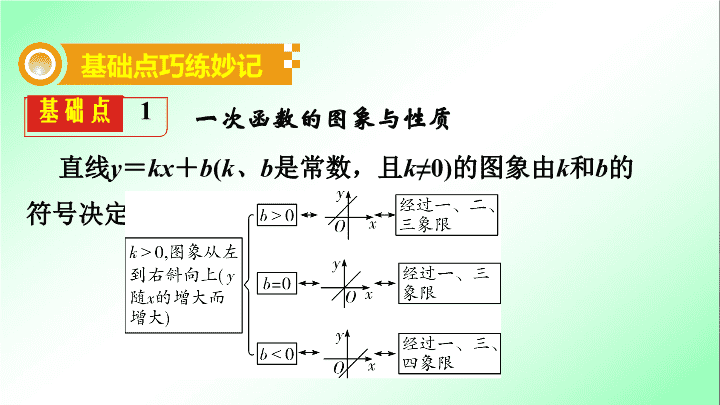
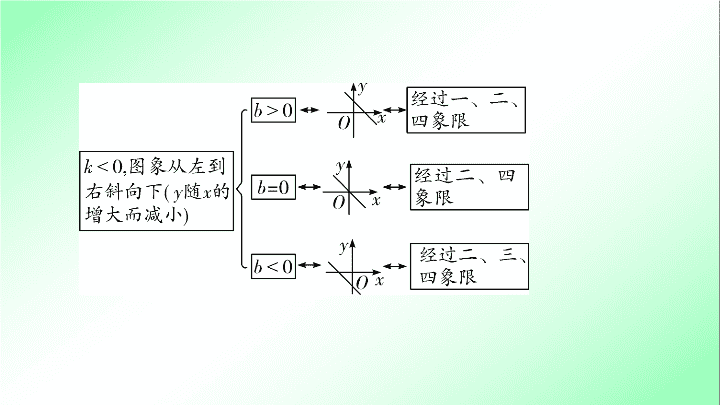
第一部分 夯实基础　提分多 第 三 单元 函数 第1 1 课时 一次函数及其应用 直线 y ＝ kx ＋ b ( k 、 b 是常数，且 k ≠0) 的图象由 k 和 b 的符号决定： 基础点 1 一次函数的图象与性质 基础点巧练妙记 一次函数 y ＝ kx ＋ b ( k ≠ 0) 与坐标轴的交点坐标： 与 x 轴的交点坐标：令 y ＝ 0 ，得 x ＝－ ，则交点坐标为 ( － ， 0) ； 与 y 轴的交点坐标：令 x ＝ 0 ，则 y ＝ b ，则交点坐标为 (0 ， b) ；特别地，正比例函数经过原点 (0 ， 0) ．            练 提 分 必 1. 已知函数 y ＝ kx 的函数值随 x 的增大而增大，则函数的图象经过 ( 　　 ) A. 第一、二象限 B. 第一、三象限 C. 第二、三象限 D. 第二、四象限 B            练 提 分 必 2 ．关于直线 l ： y ＝ kx ＋ k ( k ≠0) ，下列说法不正确的是 ( 　 ) A ．点 (0 ， k ) 在 l 上 B ． l 经过定点 ( － 1 ， 0) C ．当 k ＞ 0 时， y 随 x 的增大而增大 D ． l 经过第一、二、三象限 D            练 提 分 必 3 ．已知点 M (1 ， a ) 和点 N (2 ， b ) 是一次函数 y ＝－ 2 x ＋ 1 图象上的两点，则 a 与 b 的大小关系是 _______ ． 4 ．在一次函数 y ＝ (1 － m ) x ＋ 1 中，若 y 的值随 x 值的增大而减小，则 m 的取值范围为 ________ ． a > b m ＞ 1 1 ． 待定系数法求表达式 (1) 设： 设一次函数一般式 y ＝ kx ＋ b ； (2) 代： 把已知条件 ( 关键是图象上两个点的坐标 ) 代入解析式得到关于待定系数 k ， b 的方程 ( 组 ) ； (3) 求： 解方程 ( 组 ) ，求出待定系数 k ， b 的值； (4) 写： 依据 k ， b 值写出一次函数表达式． 基础点 2 一次函数表达式的确定 2 ．一次函数图象的平移 左右平移： y ＝ kx ＋ b y ＝ k ( x － m ) ＋ b ； 上下平移： y ＝ kx ＋ b y ＝ kx ＋ b ＋ n ， 口诀： 左加右减，上加下减． 向上平移 n 个单位 表达式右边加 n 向右平移 m 个单位 x 换为 x-m            练 提 分 必 5 ．已知一次函数的图象经过点 (2 ， 3) 和点 ( － 2 ，－ 5) ，则这个函数解析式为 ______________ ． 6 ．把直线 y ＝ 2 x － 1 向上平移 2 个单位，所得直线的解析式是 ____________ ；再将平移后的解析式向左平移 3 个单位，所得直线的解析式是 ____________ ． y ＝ 2 x － 1 y ＝ 2 x ＋ 1 y ＝ 2 x ＋ 7 1 ． 一次函数与一次方程 ( 组 ) 的关系 (1) 一次函数 y ＝ ax ＋ b ( a ， b 是常数， a ≠0) 的图象与① ______ 交点的横坐标⇔一元一次方程 ax ＋ b ＝ 0 的解； (2) 两个一次函数图象的交点坐标⇔两个一次函数表达式所组成的二元一次方程组的解． 基础点 3 一次函数与方程 ( 组 ) 、不等式的关系 x 轴 2 ． 一次函数与一元一次不等式的关系 (1) 如图①，不等式 kx ＋ b >0 的解集⇔一次函数图象位于 x 轴上方部分对应 x 的取值范围；不等式 kx ＋ b <0 的解集⇔一次函数图象位于 x 轴下方部分对应 x 的取值范围； 图① (2) 如图②，设点 C 的坐标为 ( m ， n ) ，那么不等式 k 1 x ＋ b 1 ≤ k 2 x ＋ b 2 的解集是 ② _______ ． x≥m 图② 重难点精讲优练 类型 1 一次函数的图象与性质 例 1 　 已知一次函数 y ＝ 2 x ＋ 4. (1) 在如图所示的平面直角坐标系中，画出函数的图象； 例 1 题图 例 1 题解图 解： (1) 如解图 (2) 求图象与 x 轴的交点 A 的坐标，与 y 轴的交点 B 的坐标； 解： 对于 y ＝ 2 x ＋ 4 ，令 x ＝ 0 ，则 y ＝ 4 ； 令 y ＝ 0 ，则 x ＝－ 2 ， 函数图象 y ＝ 2 x ＋ 4 经过 (0 ， 4) ， ( － 2 ， 0) 两点， ∴ A ( － 2 ， 0) ， B (0 ， 4) ； (3) 在 (2) 条件下，求△ AOB 的面积； 解： ∵ A ( － 2 ， 0) ， B (0 ， 4) ， ∴ OA ＝ 2 ， OB ＝ 4 ， ∴ S △ AOB ＝ • OA • OB ＝ ×2×4 ＝ 4 ， 故△ AOB 的面积为 4 ； (4) 利用图象直接写出：当 y ＜ 0 时， x 的取值范围． 【 解法提示 】 由函数图象可看出，当 x ＜－ 2 时，函数图象在 x 轴的下方，此时 y ＜ 0 ；当 x ＞－ 2 时，函数图象在 x 轴的上方，此时 y ＞ 0 解： x ＜－ 2. 练习 1 　 已知一次函数 y ＝ kx ＋ b － x 的图象与 x 轴的正半轴相交，且函数值 y 随自变量 x 的增大而增大，则 k ， b 的取值情况为 ( 　　 ) A .k ＞ 1 ， b ＜ 0 B . k ＞ 1 ， b ＞ 0 C. k ＞ 0 ， b ＞ 0 D. k ＞ 0 ， b ＜ 0 A 练习2　一次函数 y ＝ x － b 与 y ＝ x －1的图象之间的距离等于3，则 b 的值为(　　) A. －2或4 B. 2或－4 C. 4或－6 D. －4或6 【解析】 设直线 y ＝ x －1与 x 轴交点为 C ，与 y 轴交点为 A ，过点 A 作 AD ⊥直线 y ＝ x － b 于点 D ，如解图所示． 练习 2 题解图 ∵直线 y ＝ x －1与 x 轴交点为 C ，与 y 轴交点为 A ， ∴点 A (0，－1)，点 C ( ，0) ， ∴ OA ＝ 1 ， OC ＝ 34 ， AC ＝ ＝ 54 ， ∴ cos ∠ ACO ＝ ＝ 35 ， ∵∠ BAD 与∠ CAO 互余，∠ ACO 与∠ CAO 互余， ∴∠ BAD ＝∠ ACO ， ∵ AD ＝ 3 ， cos ∠ BAD ＝ ＝ ， ∴ AB ＝ 5 ， ∵直线 y ＝ x － b 与 y 轴的交点为 B (0 ，－ b) ， ∴ AB ＝ | － b － ( － 1)| ＝ 5 ， 解得： b ＝－ 4 或 b ＝ 6. 练习 3 　 已知直线 y ＝ 2 x ＋ (3 － a ) 与 x 轴的交点在 A (2 ， 0) ， B (3 ， 0) 之间 ( 包括 A 、 B 两点 ) ，则 a 的取值范围是 ________ ． 7≤ a ≤9 【 解析 】 ∵ 直线 y ＝ 2 x ＋ (3 － a ) 与 x 轴的交点在 A (2 ， 0) 、 B (3 ， 0) 之间 ( 包括 A 、 B 两点 ) ，∴ 2≤ x ≤3 ，令 y ＝ 0 ，则 2 x ＋ (3 － a ) ＝ 0 ，解得 x ＝ ，则 2≤ ≤3 ，解得 7≤ a ≤9. 类型 2 一次函数的实际应用 例 2 　 (2017 连云港 ) 某蓝莓种植生产基地产销两旺，采摘的蓝莓部分加工销售，部分直接销售，且当天都能销售完．直接销售是 40 元 / 斤，加工销售是 130 元 / 斤 ( 不计损耗 ) ．已知基地雇佣 20 名工人，每名工人只能参与采摘和加工其中一项工作，每人每天可以采摘 70 斤或加工 35 斤，设安排 x 名工人采摘蓝莓，剩下的工人加工蓝莓． (1) 若基地一天的总销售收入为 y 元，求 y 与 x 的函数关系式； 【 信息梳理 】 安排 x 名工人采摘蓝莓，则加工蓝莓人数为 (20 － x ) 名，根据题意可得： 售价 数量 收入 直接销售 40 70 x － 35(20 － x ) 加工销售 130 35(20 － x ) 40×[70x － 35(20 － x)] 130×35(20 － x) 解 ： (1)∵ 已知基地雇佣 20 名工人，安排 x 名工人采摘蓝莓， ∴加工蓝莓的工人为 (20 － x ) 名， 又∵销售总收入＝直接销售收入＋加工销售收入， ∴根据题意得： y ＝ [70 x － (20 － x )×35]×40 ＋ (20 － x )×35×130 ＝－ 350 x ＋ 63000 ； (2) 试求如何分配工人，才能使一天的销售收入最大？并求出最大值． 解 ： ∵ 70 x ≥35(20 － x ) ， 解得 x ≥203 ， 又∵ x 为正整数，且 x ≤20 ， ∴ 7≤ x ≤20 ，且 x 为正整数 ， ∵由 (1) 知 y ＝－ 350 x ＋ 63000 ，－ 350<0 ， ∴ y 随 x 的增大而减小， ∴当 x ＝ 7 时， y 取最大值， 最大值为－ 350×7 ＋ 63000 ＝ 60550. 答：安排 7 名工人进行采摘， 13 名工人进行加工，才能使一天的收入最大，最大收入为 60550 元． 例 3 　 为了追求更舒适的出行体验，利用网络呼叫专车的打车方式受到大众欢迎．据了解在非高峰期时，某种专车所收取的费用 y ( 元 ) 与行驶里程 x (km) 的函数关系如图所示，请根据图象解答下列问题： 例 3 题图 (1) 求 y 与 x 之间的函数关系式； 【 思维教练 】 根据所给函数图象可知在 0 ＜ x ≤3 和 x ＞ 3 这两段所对应的函数图象不同，可考虑分别计算 0 ＜ x ≤3 ， x ＞ 3 对应的函数关系式，根据图象上数据信息，运用待定系数法即可得出函数关系式． 【 自主解答 】 解： (1) 由函数图象可得，当 0 ＜ x ≤3 时， y ＝ 12 ， 设当 x ＞ 3 时， y 与 x 的函数关系式为 y ＝ kx ＋ b ， 根据题意得 ， 解得 ， 即 y ＝ 2.2 x ＋ 5.4 ， ∴ y 与 x 之间的函数关系式为 y ＝ 3 k ＋ b ＝ 12 8 k ＋ b ＝ 23 k ＝ 2.2 b ＝ 5.4 12 （ 0 ＜ x ≤3 ） 2.2 x ＋ 5.4 （ x ＞ 3 ） (2) 若专车低速行驶 ( 时速≤ 12 km/h) ，每分钟另加 0.4 元的低速费 ( 不足 1 分钟的部分按 1 分钟计算 ) ．某乘客有一次在非高峰期乘坐专车，途中低速行驶了 6 分钟，共付费 32 元，求这位乘客乘坐专车的行驶里程． 【 思维教练 】 要求这位乘客的行驶里程，应先根据专车行驶的费用＋另外收取的低速费用＝ 32 元，判断该行驶里程属于 (1) 中的哪一区间 (0 ＜ x ≤3 或 x ＞ 3) ，然后运用相应的函 数关系式，求出 x 的值即可． 【 自主解答 】 解： 由 (1) 知若该乘客乘坐专车的行驶里程不超过 3 km ，则应付费 12 ＋ 0.4×6 ＝ 14.4( 元 ) ＜ 32( 元 ) ， ∴其行驶里程数大于 3 km ， ∴由 (1) 可得： 2.2 x ＋ 5.4 ＋ 6×0.4 ＝ 32, 解得 x ＝ 11. 答：这位乘客乘坐专车的行驶里程是 11 km . 练习 4 　 某酒厂每天生产 A 、 B 两种品牌的白酒共 600 瓶， A 、 B 两种品牌的白酒每瓶的成本和利润如下表： A B 成本 ( 元 / 瓶 ) 50 35 利润 ( 元 / 瓶 ) 20 15 设每天生产 A 种品牌的白酒 x 瓶，每天获利 y 元． (1) 请写出 y 关于 x 的函数关系式； 解： (1) 由题意可知：每天生产 A 种品牌的白酒 x 瓶，则每天生产的 B 种品牌的白酒 (600 － x ) 瓶， 则有： y ＝ 20 x ＋ 15(600 － x ) ＝ 5 x ＋ 9000 ， 其中 ，解得 0≤ x ≤600 ， x 为整数， ∴ y 关于 x 的函数关系式： y ＝ 5 x ＋ 9000(0≤ x ≤600 ， x 为整 x ≥0 600 － x ≥0 数 ) ； (2) 如果该酒厂每天至少投入成本 26400 元，那么每天至少获利多少元？ 解： 由题意可知： 50 x ＋ 35(600 － x )≥26400(0≤ x ≤600 ， x 为整数 ) ， 解得： x ≥360 ， ∴ x 的范围为： 360≤ x ≤600 ，且 x 为整数， ∵每天获利 y ＝ 5 x ＋ 9000 ， y 随着 x 的增大而增大， ∴ x ＝ 360 时， y 有最小值为 10800 元． 答：该酒厂每天至少获利 10800 元．            导 方 法 指 1 ．求函数解析式，先设函数解析式 y ＝ kx ＋ b ： ①文字型：从题干中，提取两组有关的量 ( 不同的自变量及对应的函数值 ) ，将其代入解析式中列方程组求解；            导 方 法 指 ②表格型：运输分配类表格一般涉及到两种货物和两个目的地，使用 x 分别表示出两种货物分别运往两个目的地的数量，然后写出函数解析式．自变量和函数值的对应表格则直接从表格中任选 2 组对应值，使用待定系数法求解析式；            导 方 法 指 ③图象型：任意找出函数图象上的两个点，常用到的有图象与坐标轴的交点，起点，转折点，终点等；将其坐标分别代入解析式中列方程组求出函数解析式；若函数图象为分段函数，注意要选同一段函数图象上两点坐标，代入求值，依照此方法分别计算出各段函数的解析式，最后记得加上各段函数图象对应的自变量的取值范围；            导 方 法 指 2 ．利润最大或费用最小问题： 此类问题都是利用一次函数增减性来解决，在自变量的取值范围内，根据函数图象的增减性及自变量取值，确定函数的最小 ( 大 ) 值；            导 方 法 指 3 ．方案选取问题：通常每种方案对应一个一次函数解析式 ①求最大或最小值：根据解析式分类讨论，比较各种方案在给定的自变量取值下的最优结果；            导 方 法 指 ②写出最优方案：根据题意列不等式求出自变量的取值，再看题中给出的自变量值在哪个范围内，进而选取方案． 温馨提示：点击完成练习册 word 习题