- 332.00 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
27.2 与圆有关的位置关系
2.直线与圆的位置关系
知|识|目|标
1.经历探索直线和圆的位置关系的过程,了解直线和圆的三种位置关系.
2.通过观察、思考,会利用圆心到直线的距离判断直线和圆的位置关系.
3.在掌握了直线和圆的位置关系的基础上,会应用直线和圆的位置关系求半径的值或取值范围.
目标一 了解直线和圆的位置关系
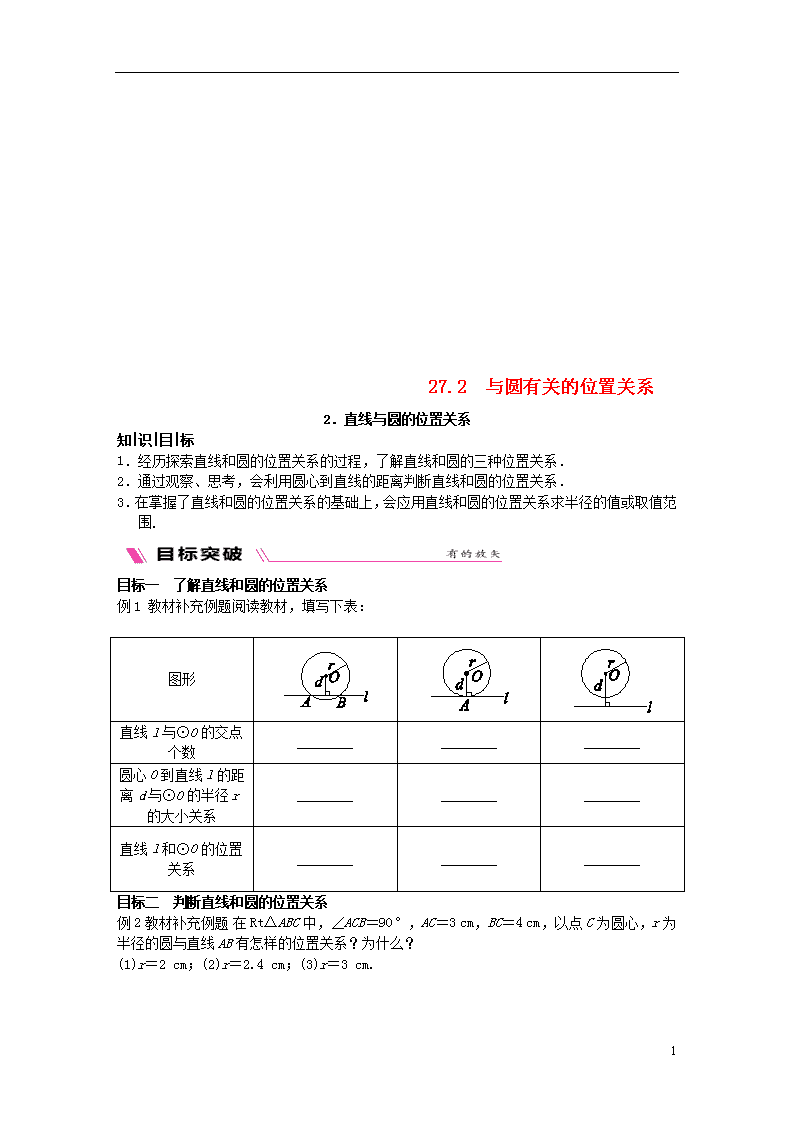
例1 教材补充例题阅读教材,填写下表:
图形
直线l与⊙O的交点个数
________
________
________
圆心O到直线l的距离d与⊙O的半径r的大小关系
________
________
________
直线l和⊙O的位置关系
________
________
________
目标二 判断直线和圆的位置关系
例2 教材补充例题 在Rt△ABC中,∠ACB=90°,AC=3 cm,BC=4 cm,以点C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
4
【归纳总结】判断直线和圆的位置关系的“三个步骤”:
图27-2-3
目标三 由直线与圆的位置关系求半径的值或取值范围
例3 教材补充例题 如图27-2-4,在Rt△ABC中,∠C=90°,AC=3,AB=5,若以点C为圆心,r为半径作圆,则:
(1)当直线AB与⊙C相切时,求r的值;
(2)当直线AB与⊙C相离时,求r的取值范围.
图27-2-4
【归纳总结】根据直线和圆的位置关系求圆的半径的值或取值范围的步骤:
(1)过圆心作已知直线的垂线;
(2)求出圆心到直线的距离;
(3)根据直线与圆的位置关系求出半径的值或取值范围.
4
知识点一 直线与圆的位置关系及有关概念
(1)如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离(如图27-2-5①).
(2)如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆________(如图27-2-5②),此时这条直线叫做圆的________,这个公共点叫做________;
(3)如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆________(如图27-2-5③),此时这条直线叫做圆的________.
图27-2-5
[注意] 直线与圆相切是指直线与圆有一个并且只有一个公共点.
知识点二 利用圆心到直线的距离d与圆的半径r的大小关系确定直线和圆的位置关系
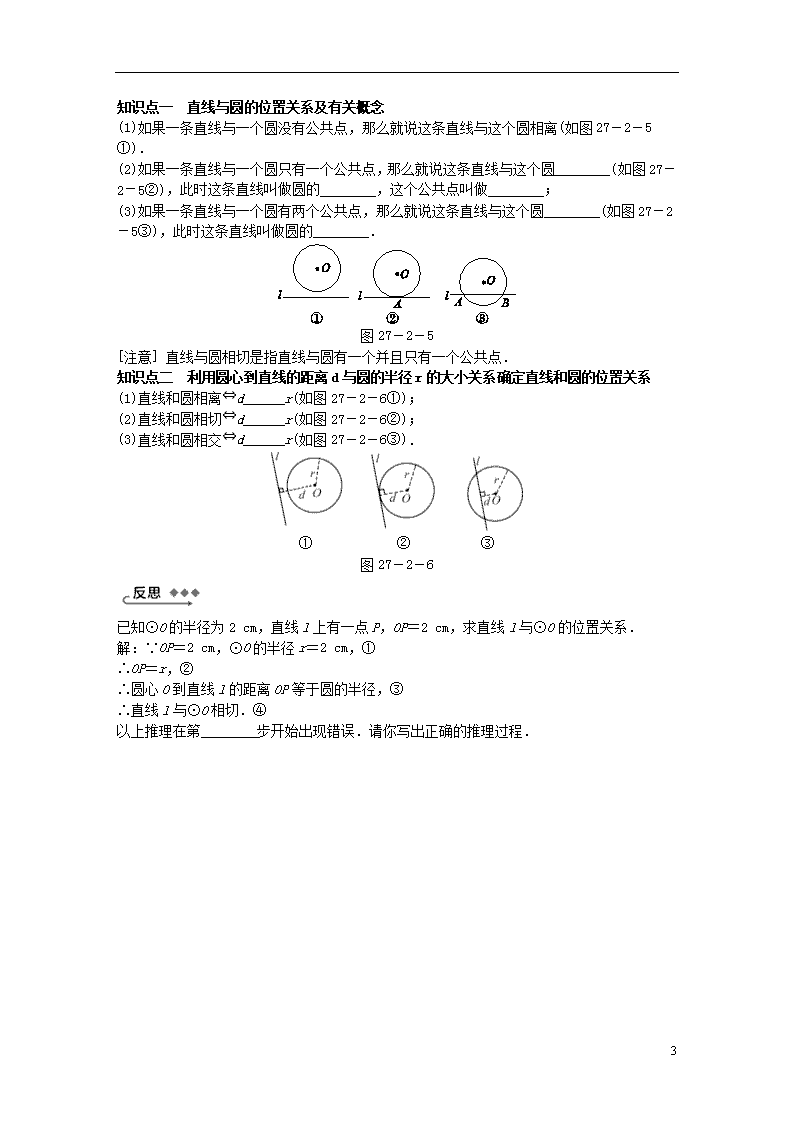
(1)直线和圆相离⇔d______r(如图27-2-6①);
(2)直线和圆相切⇔d______r(如图27-2-6②);
(3)直线和圆相交⇔d______r(如图27-2-6③).
① ② ③
图27-2-6
已知⊙O的半径为2 cm,直线l上有一点P,OP=2 cm,求直线l与⊙O的位置关系.
解:∵OP=2 cm,⊙O的半径r=2 cm,①
∴OP=r,②
∴圆心O到直线l的距离OP等于圆的半径,③
∴直线l与⊙O相切.④
以上推理在第________步开始出现错误.请你写出正确的推理过程.
4
教师详解详析
【目标突破】
例1 [答案] 2 1 0 dr 相交 相切 相离
例2 解:过点C作CD⊥AB于点D.
∵∠ACB=90°,
∴AB==5 cm.
∵AC·BC=AB·CD,
∴CD=d=2.4 cm.
(1)∵当r=2 cm时,d>r,
∴⊙C与直线AB相离.
(2)∵当r=2.4 cm时,d=r,
∴⊙C与直线AB相切.
(3)∵当r=3 cm时,dr,
∴0 (2)= (3)<
[反思] ③ 正确的推理过程如下:
∵OP=2 cm,⊙O的半径r=2 cm,
∴OP=r.
当OP⊥l时,圆心O到直线l的距离d=r,此时直线l与⊙O相切;当OP不垂直于l时,圆心O到直线l的距离d<r,此时直线l与⊙O相交.故直线l与⊙O的位置关系是相切或相交.
4
相关文档
- 2020九年级数学下册 二次函数的图2021-11-104页
- 2020九年级数学下册 二次函数的图2021-11-105页
- 华师版数学九年级下册课件-第26章 2021-11-1022页
- 福建专版2020中考数学复习方案第三2021-11-1034页
- 华师版数学九年级下册课件-第26章 2021-11-1033页
- 中考数学总复习专题课件:二次函数的2021-11-0610页
- 2020九年级数学下二次函数的图象与2021-11-066页
- 江西专版2020中考数学复习方案第三2021-11-068页
- 2020九年级数学下册 二次函数的图2021-11-064页
- 2020九年级数学下册 第26章 二次函2021-11-064页