广东省深圳市罗湖区2020-2021学年九年级上学期期末考数学试卷(Word版详解) 8页

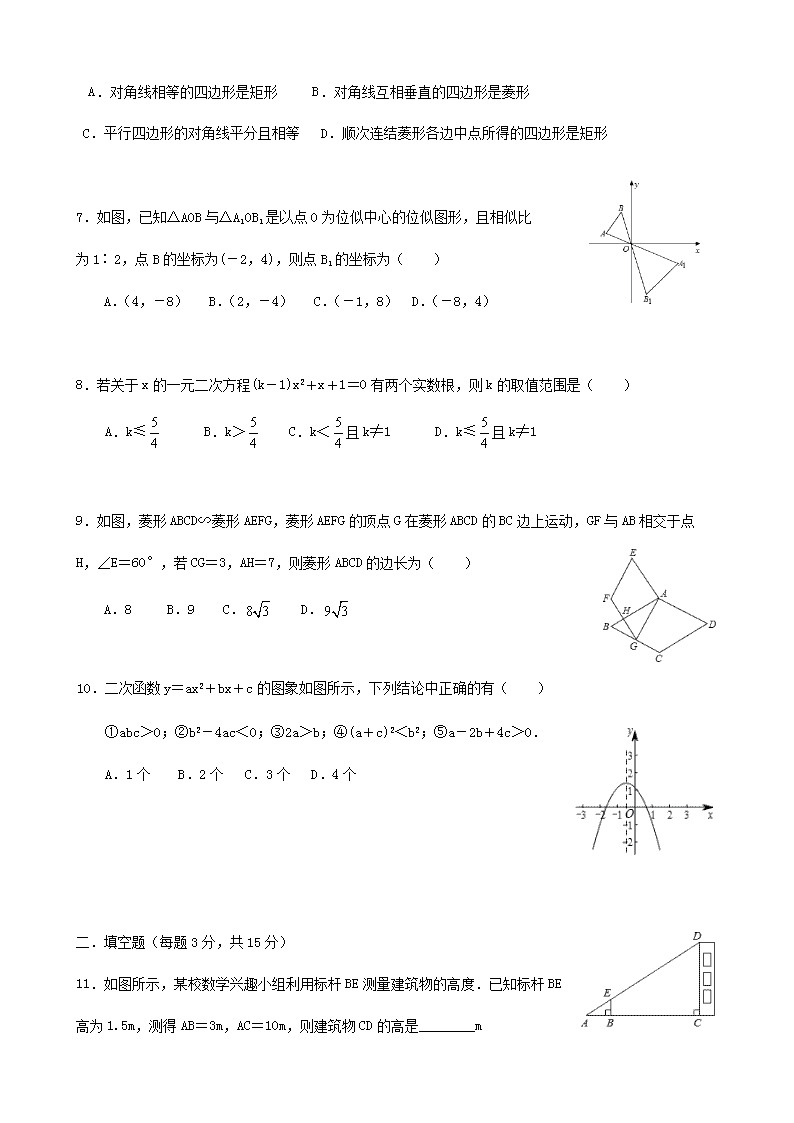
2020-2021 学年罗湖区九上期末考数学试卷(Word 版详解) 一．选择题（每题 3 分，共 30 分） 1．一元二次方程 x 2 ＋2x＝0的解是（ ） A．x1＝x2＝－2 B．x1＝2，x2＝0 C．x1＝－2，x2＝0 D．x1＝2，x2＝－2 2．下面立体图形中，从正面、侧面、上面看，都不能看到长方形的是（ ） A．长方体 B．圆柱 C．圆锥 D．正四棱锥 3．在同一副扑克牌中抽取 2张“方块”，3 张“梅花”，1 张“红桃”，将这 6张牌背面朝上，从中任意 抽取 1 张，是“梅花”的概率为（ ） A． B． C． D． 4．若反比例函数 y＝ ‸ㄴ 的图象分布在第二、四象限，则 k 的取值范围是（ ） A．k＜－2 B．k＜2 C．k＞－2 D．k＞2 5．国家实施“精准扶贫”政策以来，很多贫困人口走向了致富的道路．某地区 2017 年底有贫困人口 10 万人，通过社会各界的努力，2019 年底贫困人口减少至 1 万人．设 2017 年底至 2019 年底该地区贫困人 口的年平均下降率为 x，根据题意列方程得（ ） A．10(1－2x)＝1 B．10(1－x) 2 ＝1 C．10(1＋2x)＝D．10(1＋x) 2 ＝1 6．下列命题中，真命题是（ ） A．对角线相等的四边形是矩形 B．对角线互相垂直的四边形是菱形 C．平行四边形的对角线平分且相等 D．顺次连结菱形各边中点所得的四边形是矩形 7．如图，已知△AOB 与△A1OB1是以点 O为位似中心的位似图形，且相似比 为 1∶2，点 B的坐标为(－2，4)，则点 B1的坐标为（ ） A．（4，－8） B．（2，－4） C．（－1，8） D．（－8，4） 8．若关于 x 的一元二次方程(k－1)x 2 ＋x＋1＝0 有两个实数根，则 k的取值范围是（ ） A．k≤ 5 4 B．k＞ 5 4 C．k＜ 5 4 且 k≠1 D．k≤ 5 4 且 k≠1 9．如图，菱形 ABCD∽菱形 AEFG，菱形 AEFG 的顶点 G 在菱形 ABCD 的 BC 边上运动，GF 与 AB 相交于点 H，∠E＝60°，若 CG＝3，AH＝7，则菱形 ABCD 的边长为（ ） A．8 B．9 C．8 3 D．9 3 10．二次函数 y＝ax 2 ＋bx＋c的图象如图所示，下列结论中正确的有（ ） ①abc＞0；②b 2 －4ac＜0；③2a＞b；④(a＋c) 2 ＜b 2 ；⑤a－2b＋4c＞0． A．1个 B．2 个 C．3个 D．4 个 二．填空题（每题 3 分，共 15 分） 11．如图所示，某校数学兴趣小组利用标杆 BE 测量建筑物的高度．已知标杆 BE 高为 1.5m，测得 AB＝3m，AC＝10m，则建筑物 CD 的高是________m 12．将抛物线 y＝－2x 2 ＋5向左平移 1 个单位长度，再向下平移 2 个单位长度，所得到的抛物线为____ 13．已知 a，b 为有理数，如果规定一种新的运算“※”，规定：a※b＝3b－5a，例如：1※2＝3×2－5 ×1＝6－5＝1，计算：(2※3)※5＝________． 14．如图，在平面直角坐标系中，菱形 OABC 的边 OA 在 x 轴上，OA＝5，tan∠COA＝ 4 ．若反比例函数 y＝ k x (k＞0，x＞0)经过点 C，则 k 的值等于________． 15．如图，矩形 ABCD 中，AE＝ AD，将△ABE 沿 BE 折叠后得到△GBE，延长 BG 交 CD 于 F 点，若 CF＝FD＝3， 则 BC 的长为________． 三．解答题（共 7小题，共 55 分） 16．（5 分）计算： 11( ) 2 － －2tan45°＋4sin60°－ 2 12 ． 17．（6 分）化简分式：( 2 2 3 6 9 a a a a － － ＋ ＋ 2 3 a－ )÷ 2 2 9 a a － － ，并在 2，3，4，5 这四个数中取一个合适的数作为 a 的值代入求值． 18．（8 分）在刚刚结束的“东门 68 小时不打烊”活动中，某商场为了扩大销售额，举办抽奖活动，规则 如下：在不透明的袋子中有 2 个红球和 2个黑球，这些球除颜色外都相同，顾客每次摸出一个球，若摸 到红球，则获得 1份奖品，若摸到黑球，则没有奖品． （1）如果小芳只有一次摸球机会，那么小芳获得奖品的概率为________； （2）如果小芳有两次摸球机会(摸出后不放回)，求小芳获得 2份奖品的概率．（请用“画树状图”或“列 表”等方法写出分析过程） 19．（8 分）如图，一次函数 y＝－x＋3 的图象与反比例函数 y＝ k x (k≠0)在第一象限的图象交于 A(1，a) 和 B 两点，与 x 轴交于点 C． （1）求反比例函数的解析式； （2）求 AB BC 的值． 20．（8 分）如图，某数学兴趣小组为测量一棵古树 BH 和教学楼 CG 的高，先在 A 处用高 2 米的测角仪测得 古树顶端 H 的仰角∠HDE 为 45°，此时教学楼顶端 G 恰好在视线 DH 上，再向前走 6 米到达 B 处，又 测得教学楼顶端 G的仰角∠GEF 为 60°，点 A、B、C 三点在同一水平线上． （1）计算古树 BH 的高； （2）计算教学楼 CG 的高．（结果保留根号） 21．（10 分）如图，在平面直角坐标系中，矩形 OABC 中，OA＝8，OC＝6，点 D是对角线 AC 的中点，过点 D 的直线分别交 OA、BC 边于点 E、F． （1）求证：四边形 EAFC 是平行四边形； （2）当 CE＝CF 时，求 EF 的长； （3）在条件（2）的情况下，点 P 为 x 轴上一点，当以 E、F、P 为顶点的三角形是等腰三角形时，请求出点 P 的坐标． 22．（10 分）在平面直角坐标系中，抛物线 y＝ax 2 ＋bx＋c 经过点 A、B、C，已知 A（－1，0），B（6，0）， C（0，－6）． （1）求此抛物线的函数表达式； （2）若点 D 为第四象限内抛物线上一动点，当△BCD 面积最大时，求△BCD 面积最大值； （3）在 x 轴上是否存在点 M，使∠OCM＋∠ACO＝45°，若存在，请求出点 M 的坐标；若不存在，请说明理 由． 答案详解 1. 解析：解一元二次方程可得 x=0 或-2,选 C 2. 解析：圆锥的三视图分别是圆和三角形，故选 C 3. 解析：依概率公式可解答。故选 C 4. 解析：反比例函数位于第二、四象限时，2-k<0,k>2，故选 D 5. 解析：依元二次方程增长率应用题公式解答，故选 B 6. 解析：选项 A:可能是筝形;选项 B:可能是筝形;选项 C:平行四边形对角线只平分;故选 D 7.解析：当位似中心是原点时，位似图形的对应点的对应坐标之比就是相似比，注意符号。故选 A 8. 解析：由题可得△≥0且 k-1≠0,故选 D 9.解析：中等难度题，菱形典型题型：含特殊角的菱形计算题型：盯特殊三角形. 连接 AC，由题易知△ABC 是等边三角形，则 AB=BC=AC，找含有 CG、AH、与菱形边长联系最紧密的三角 形相似，不难找到△BGH 与△CAG，由外角定理可得∠BHG=∠AGC=60º+∠HAG，∠B=∠ACG=60º， 由△BGH∽△CAG，可得 BG AC = BH CG ，即 BC‸ BC = BC‸7 ,解得 BC=9，故选 B 10. 解析：由开口方向可知 a<0，由对称轴“左同右异”可知 b<0，与 y 轴交于下半轴可知 c>0 （1）则 abc>0,①正确； （2）图像与 x 轴有两个交点，则b ‸ 4ac > 0，②错误； （3）对称轴 y =‸ b a >‸ 可得 b a < 可得 b>2a，③错误； （4）原式可变形为(a + c) ‸ b < 0，即(a+b+c)(a-b+c)<0；由图可知当x=1时 a+b+c<0，当x=-1时，a-b+c>0, ∴(a+b+c)(a-b+c)<0,④正确； （5）a-2b+4c=2(a-b+c)-a+2c,∵a-b+c>0, -a >0, 2c>0,∴2(a-b+c)-a+2c>0，⑤正确 综上所述，正确结论是①④⑤，选 C 11. 解析：由相似的“A字模型”可得： BE AB = DC AC ，得 DC=5m 12. 解析：依平移规律可得y =‸ (x + )+5-2=y =‸ (x + ) + 13. 解析：定义新运算题型。分步算：2※3＝3×3－5×2＝-1，-1※5＝3×5－5×（-1）＝20 14. 解析：有三角函数，必构造 Rt△,故作 CD⊥x 轴于点 D，由 OC=OA=5, tan∠COA＝ 4 易得 OD=4,CD=3，则 C（4，3）,则 k=12 15.解析：数学典型题型：折叠问题. （一）代数方法（解方程）：折叠性质+方程思路+勾股定理或相似. 由折叠性质及方程思路可表示出如图各边，在 Rt△BCF 中，由勾股定理得： + (a) = ( + 9 + a). 方程看似复杂，其实很好解，过程如下： 去平方得：9+9a=36+12 9 + a+9+a，化简得 9 + a=a ‸ 两边平方得：36+12a=a4 ‸ a + ,得a=24，得 a=2 ，则 BC=6 （二）几何方法（相似）题目条件中出现“AE＝ AD”,即 AE:AD=1:3,相似典型题型：“线段比问题”，构 造三角形相似，利用相似性质解题. 作 EN⊥BC 于点 N，交 BF 于点 M，由 MN//CF 可得 BM BF = MN FC = BN BC = AE AD = ,∵CF=3,∴MN=1，由 BN=AE=EG，∠ BMN=∠EMG,∠BNM=∠EGM 可得△BNM≌△EGM，则 MG=MN=1，则 BM=BG-MG=AB-MG=6-1=5，由 BM BF = 可得 FB=15，在 Rt△BCF 中由勾股定理可得 BC==6 . 16. 解析：原式=2-2×1+4× -2×2 =-2 17. 解析：原式= (a‸)(a‸) (a‸)(a‸) × (a+)(a‸) a‸ = a + ,∵a≠3,a≠2,∴当 a=4 时，原式=7；或当 a=5 时原式=8 18. 解析：（1）由概率公式可解答：小芳获得奖品的概率为 （2））画树状图为： 共有 12 种等可能的结果数，其中两次摸到红球的结果数为 2，所以两次摸到红球的概率＝ ． 19. 解析：（1）将 A 点坐标代入一次函数中可得 a=2，则 k=1×2=2,反比例函数解析式为 y= x （2）联立方程 y = x y＝－x＋ ，可得 B 点坐标为（2，1）.由一次函数可得 C 点坐标为（3，0）， 由两点间的距离公式可得 AB= ,BC= ,∴ AB BC = 20. 解析：（1）由题可知 AD=BE=2 米，DE=6 米，△EDH 是等腰直角三角形，则 EH=DE=6 米，∴BH=8 米； （2）设 GF=x 米，在 Rt△EFG 中，由 tan60º= x EF可得 EF= x，由 EH//CG 可得 DE DF = EH GF ，即 + x = x，解得： x=9+3 ,∴CG=9+3 +2=11+3 21.解析：（1）△CDF≌△ADE（ASA）可得 DE=DF，由对角线互相平分的四边形是平行四边形可得四边形 EAFC 是平行四边形。 （2）当 CE=CF时，平行四边形EAFC是菱形。设 OE=a，则 AE=CE=8-a，在 Rt△OCE中，由勾股定理可得 + a = (8 ‸ a)，解得 a= 7 4 ,则 AE=CF=8- 7 4 = 5 4 ，可得 E( 7 4 ,0),F( 5 4 ,6)，由两点之间的公式可得 EF= 5 （3）初二的“两圆一线”即可求解 ①当 EF=EP= 5 时，（以点 E为圆心，EF 为半径画圆，交 x 轴于点P、P）则 OP=EP-OE= 5 - 7 4 = 4 , OP=EP+OE= 5 + 7 4 = 7 4 ,∴P( ‸ 4 ,0)、P( 7 4 ,0) ②当 FE=FP 时，（以点 F 为圆心，EF 为半径画圆，交 x轴于点P）作 FM⊥x 轴于点 M，则 EM=MP=4,则 OP=OE+EP= 7 4 +8= 9 4 ,∴ P( 9 4 ,0) ③当 PE=PF 时，∵四边形 AECF 是菱形，AE=AF，则 P 与 A 重合，∴P4(8,0) 综上所述，P的坐标为P( ‸ 4 ,0)、P( 7 4 ,0)、( 9 4 ,0)或（8，0） 22.解析：（1）设交点式，代入点 B 坐标即可得抛物线解析式：y = x ‸ 5x ‸ （2） “铅垂法”+配方法解题。 如图 1 作 DE//y 轴交 BC 于点 E，设 D(a, a ‸ 5a ‸ )，由 B,C 可得直线 BC 的解析式为 y=x-6，则 E （a,a-6），则 DE=a-6-(a ‸ 5a ‸ )=‸ a + a, 则S∆BCD = OB ∙ DE = × ‸ a + a =‸ a + 8a =‸ a ‸ ++ 7，当 a=3 时，S∆BCD有最 大值，最大值为 27. （3）二次函数典型题型：点角存在性问题。先把角的和差问题转化成一个角的问题，再按点角存在性问 题的典型思路解题。 由 B,C 两点坐标可知，∠OCB=45º, ①当点 M在 y轴右侧时，∠OCM＋∠ACO＝45°，∠OCM+∠BCM=45º,∴∠ACO=∠BCM，则 tan∠ACO=tan ∠BCM= OA OC = ，作 BF⊥BC 交 CM 于点 F，过 B 作 GP⊥x 轴，作 FG⊥GP 于点 G，作 CP⊥GP 于点 P，则由“一 线三垂直模型”易得△FGB∽△BPC，则 FG BP = GB CP = FB BC = tan∠BCM = ,∵CP=BP=6，∴FG=GB=1,∴F(5,1), ∴直线 CF 的表达式为 y= 7 5 x ‸ ,∴M( 0 7 ，0) ②作 M 关于点 O 的对称点 M`，连接 CM`，则∠OCM=∠OCM`，由∠OCM＋∠ACO＝45°可得∠OCM`＋∠ACO＝ 45°，点 M`符合题目要求，则 M`(‸ 0 7 ，0) 综上所述，点 M 的坐标为( 0 7 ，0)或(- 0 7 ，0)