九年级数学上册第四章图形的相似8图形的位似教学案无答案新版北师大版 2页

‎4.8 图形的位似 ‎【教学目标】‎ 知识与技能 掌握位似图形的定义并掌握位似图形的性质；‎ 过程与方法 学生经历将一个图形放大或缩小的方法，并且在学习和运用过程中发展数学应用意识。‎ 情感、态度与价值观 培养学生动手操作的良好习惯，以积极进取的思想探究数学学科知识，体会本节知识的实际应用价值和文化价值。‎ ‎【教学重难点】‎ 教学重点：能够利用作位似图形等方法将一个图形放大或缩小。‎ 教学难点：位似图形的画法。‎ ‎【导学过程】‎ ‎【创设情景，引入新课】‎ 展示课件：是上海高楼的画面，演示图片的缩放过程。‎ ‎　　（回顾相似多边形的有关概念和性质，为新课引入进行铺垫，同时渗透爱国主义教育，激发学生的学习兴趣和爱国热情）‎ ‎【自主探究】‎ 操作实验：指导全班同学动手操作、进行实验，每位同学拿出自备的两个相似图形纸片，位置任意摆放，连接对应点，观察对应点的连线是否经过一点。同时请三位同学上黑板前台选取不同类型的相似图形（三角形、四边形、五边形）进行演示，供班级同学参考并猜想。‎ 这几副图片表示出了图形之间的什么特殊的关系？‎ ‎【课堂探究】‎ 建构新知：位似图形及其有关概念 如果两个图形不仅是相似图形，而且每组对应点所在的直线都经过同一个点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，这时的相似比又称为位似比.‎ ‎　　2、让学生进一步操作，亲身感受位似图形与相似图形的联系与区别。通过观察、思考、交流、讨论得出如下结论：‎ ‎　　位似图形是一种特殊的相似图形，而相似图形未必都能构成位似关系。‎ ‎　　（引导学生动手、动脑，观察、思考，感悟知识的生成和变化）‎ ‎　　3、认一认：‎ ‎　　见课本97页图3--36，3--37（1）、（2）、辨认位似图形，并指认位似中心。‎ ‎　　（从正反两个方面强化学生对位似图形的认识）‎ 2‎ ‎　　4、练一练：‎ ‎　　例1 下列说法正确的是（ ）‎ ‎　　A.两个图形如果是位似图形，那么这两个图形一定全等；‎ ‎　　B.两个图形如果是位似图形，那么这两个图形不一定相似；‎ ‎　　C.两个图形如果是相似图形，那么这两个图形一定位似；‎ ‎　　D.两个图形如果是位似图形，那么这两个图形一定相似。‎ ‎　　例：如图已知△ABC以点O为位似中心画△DEF，使它与△ABC相似，相似比为2.‎ C 在平面直角坐标系中△OAB的顶点坐标分别是O(0,0),A(3,0),B(2,3),将点O,A,B的横，纵坐标都乘2.以这三个点为顶点的三角形与△OAB位似吗？如果位似。指出位似中心和相似比。‎ 如果将点O,A,B的横，纵坐标都乘-2呢？‎ ‎【当堂训练】‎ 1． 如图，已知△ABC和点O.以O为位似中心，‎ 求作△ABC的位似图形，并把△ABC的边长 缩小到原来的一半. 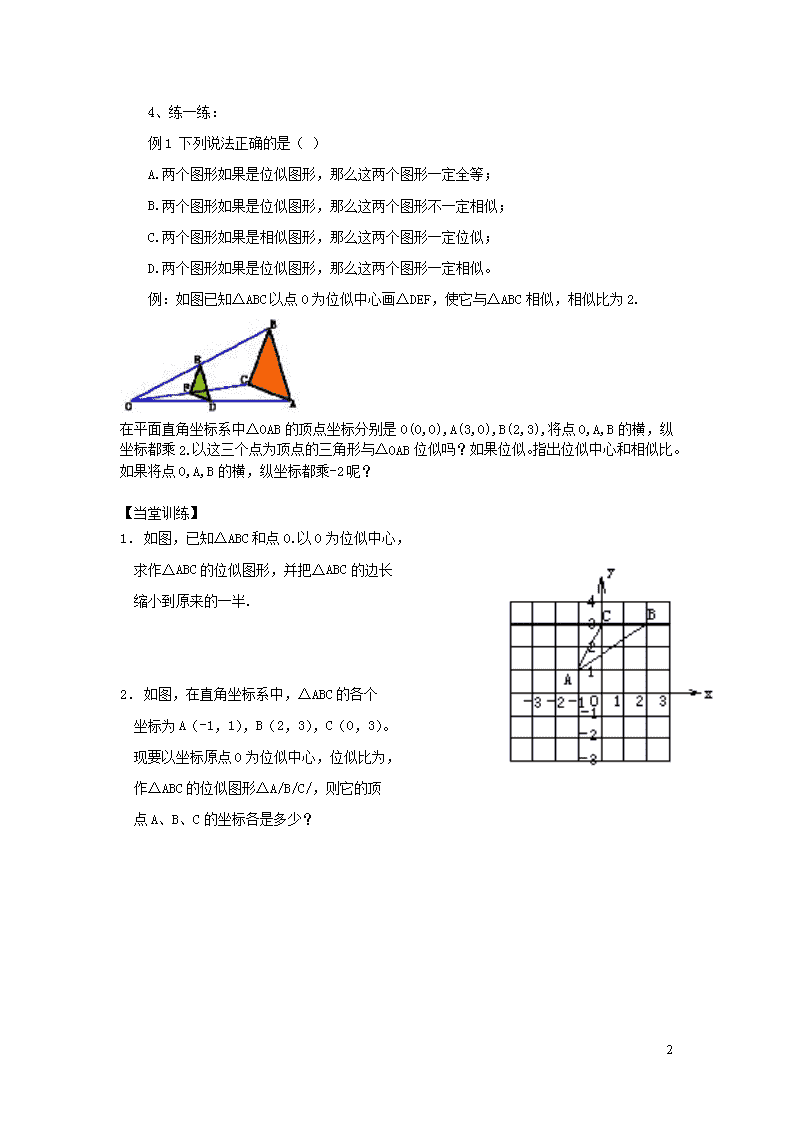‎ 2． 如图，在直角坐标系中，△ABC的各个 坐标为A（-1，1），B（2，3），C（0，3）。‎ 现要以坐标原点0为位似中心，位似比为，‎ 作△ABC的位似图形△A/B/C/，则它的顶 点A、B、C的坐标各是多少？‎ 2‎