- 446.50 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第四章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如果mn=ab,那么下列比例式中错误的是( C )
A.= B.= C.= D.=
2.(2019·沈阳)已知△ABC∽△A′B′C′,AD和A′D′是它们的对应中线,若AD=10,A′D′=6,则△ABC与△A′B′C′的周长比是( C )
A.3∶5 B.9∶25 C.5∶3 D.25∶9
3.(哈尔滨中考)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( D )
A.= B.= C.= D.=
4.(2019·玉林)如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( C )
A.3对 B.5对 C.6对 D.8对
5.在中华经典美文阅读中,刘明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm,则它的宽约为( A )
A.12.36 cm B.13.6 cm C.32.36 cm D.7.64 cm
6.(2019·巴中)如图▱ABCD,F为BC中点,延长AD至E,使DE∶AD=1∶3,连结EF交DC于点G,则S△DEG:S△CFG=( D )
A.2∶3 B.3∶2 C.9∶4 D.4∶9
7.(2019·锦州)在矩形ABCD中,AB=3,BC=4,M是对角线BD上的动点,过点M作ME⊥BC于点E,连接AM,当△ADM是等腰三角形时,ME的长为( C )
A. B. C.或 D.或
8.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( D )
A.-a B.-(a+1) C.-(a-1) D.-(a+3)
9.(2019·贵港)如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( C )
A.2 B.3 C.2 D.5
10.(2019·东营)如图,在正方形ABCD中,点O是对角线AC,BD的交点,过点O作射线OM,ON分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG·OC.其中正确的是( B )
6
A.①②③④ B.①②③ C.①②④ D.③④
二、填空题(每小题3分,共15分)
11.若x∶y=1∶2,则=__-__.
12.(连云港中考)如图,△ABC中,点D,E分别在AB,AC上,DE∥BC,AD∶DB=1∶2,则△ADE与△ABC的面积的比为__1∶9__.
13.(2019·阜新)如图,在Rt△ABC中,∠C=90°,点D是AC边上的一点,DE垂直平分AB,垂足为点E.若AC=8,BC=6,则线段DE的长度为____.
14.(2019·烟台)如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__(-5,-1)__.
15.(2019·无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为__8__.
三、解答题(共75分)
16.(8分)(杭州中考)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
解:(1)∵AB=AC,BD=CD,∴AD⊥BC,∠B=∠C,∵DE⊥AB,∴∠DEB=∠ADC,∴△BDE∽△CAD (2)∵AB=AC,BD=CD,∴AD⊥BC,在Rt△ADB中,AD==12,∵·AD·BD=·AB·DE,∴DE=
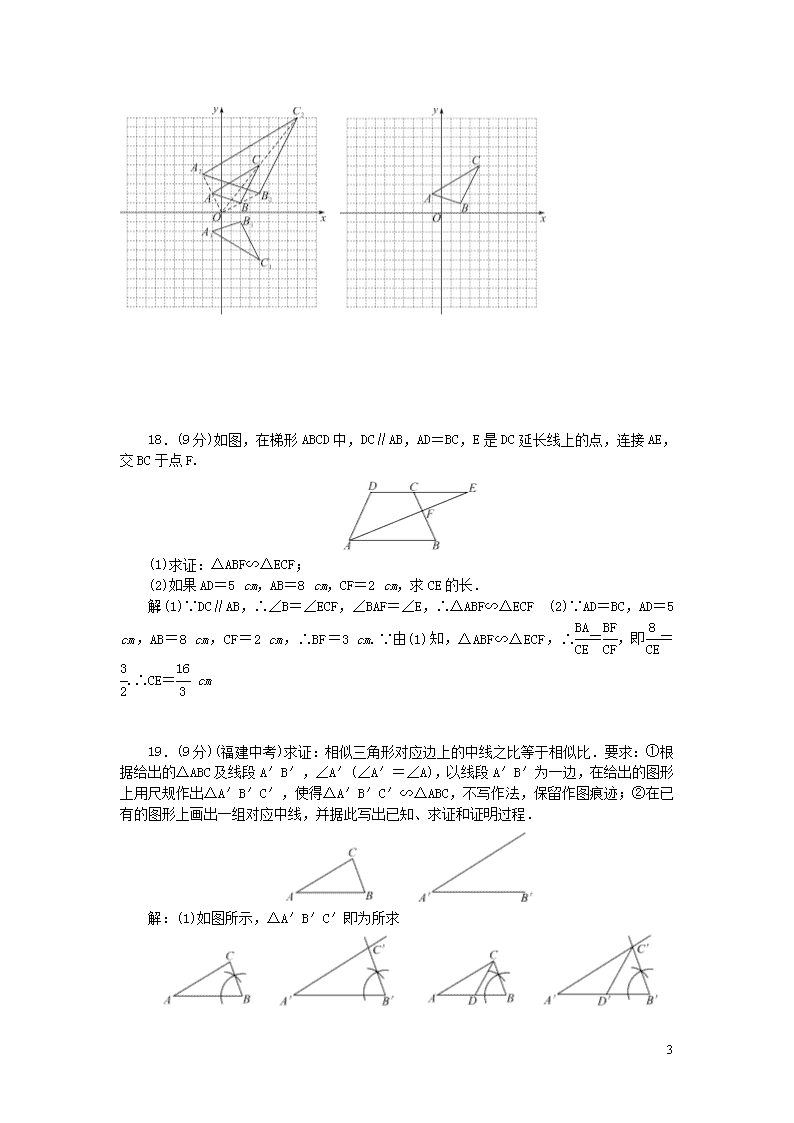
17.(9分)(凉山州中考)如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(-1,2),B(2,1),C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为2,并求出△A2B2C2的面积.
解:(1)如图所示,△A1B1C1就是所求三角形 (2)如图所示,△A2B2C2就是所求三角形.分别过点A2,C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E,F,∵A(-1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且相似比为2,∴A2(-2,4),B2(4,2),C2(8,10),∴S△A2B2C2=8×10-×6×2-×4×8-×6×10=28
6
18.(9分)如图,在梯形ABCD中,DC∥AB,AD=BC,E是DC延长线上的点,连接AE,交BC于点F.
(1)求证:△ABF∽△ECF;
(2)如果AD=5 cm,AB=8 cm,CF=2 cm,求CE的长.
解:(1)∵DC∥AB,∴∠B=∠ECF,∠BAF=∠E,∴△ABF∽△ECF (2)∵AD=BC,AD=5 cm,AB=8 cm,CF=2 cm,∴BF=3 cm.∵由(1)知,△ABF∽△ECF,∴=,即=.∴CE= cm
19.(9分)(福建中考)求证:相似三角形对应边上的中线之比等于相似比.要求:①根据给出的△ABC及线段A′B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A′B′C′,使得△A′B′C′∽△ABC,不写作法,保留作图痕迹;②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
解:(1)如图所示,△A′B′C′即为所求
6
(2)已知:如图,△ABC∽△A′B′C′,===k,D是AB的中点,D′是A′B′的中点,求证:=k.证明:∵D是AB的中点,D′是A′B′的中点,∴AD=AB,A′D′=A′B′,∴==,∵△ABC∽△A′B′C′,∴=,∠A′=∠A,∵=,∠A′=∠A,∴△A′C′D′∽△ACD,∴==k
20.(9分)(2019·雅安)如图,▱ABCD的对角线AC,BD相交于点O,EF经过O,分别交AB,CD于点E,F,EF的延长线交CB的延长线于M.
(1)求证:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的长.
解:(1)∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,BC=AD,∴∠OAE=∠OCF,在△AOE和△COF中,∴△AOE≌△COF(ASA),∴OE=OF (2)过点O作ON∥BC交AB于N,则△AON∽△ACB,∵OA=OC,∴ON=BC=2,BN=AB=3,∵ON∥BC,∴△ONE∽△MBE,∴=,即=,解得BE=1
21.(10分)晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
6
解:由题意得∠CAD=∠MND=90°,∠CDA=∠MDN,∴△CAD∽△MND,∴=,∴=,∴MN=9.6,又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,∴△EFB∽△MFN,∴=,∴=,∴EB≈1.75,∴小军身高约为1.75米
22.(10分)(2019·梧州)如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)求DE的长;
(2)求证:∠1=∠DFC.
(1)解:∵矩形ABCD中,AD∥CF,∴∠DAF=∠AFC,∵AF平分∠DAC,∴∠DAF=∠CAF,∴∠FAC=∠AFC,∴AC=CF,∵AB=4,BC=3,∴AC===5,∴CF=5,∵AD∥CF,∴△ADE∽△FCE,∴=,设DE=x,则=,解得x=,∴DE= (2)∵AD∥FH,AH∥DF,∴四边形ADFH是平行四边形,∴AD=FH=3,∴CH=2,BH=5,∵AD∥BH,∴△ADG∽△HBG,∴=,∴=,∴DG=,∵DE=,∴==,∴EG∥BC,∴∠1=∠AHC,又∵DF∥AH,∴∠AHC=∠DFC,∠1=∠DFC
23.(11分)(苏州中考)问题1:如图①,在△ABC中,AB=4,D是AB上一点(不与A,B重合),DE∥BC,交AC于点E,连接CD.设△ABC的面积为S,△DEC的面积为S′.
(1)当AD=3时,=________;
(2)设AD=m,请你用含字母m的代数式表示.
问题2:如图②,在四边形ABCD中,AB=4,AD∥BC,AD=BC,E是AB上一点(不与A,B重合),EF∥BC,交CD于点F,连接CE.设AE=n,四边形ABCD的面积为S,△EFC的面积为S′.请你利用问题1的解法或结论,用含字母n的代数式表示.
6
解:问题1:(1)∵AB=4,AD=3,∴BD=4-3=1,∵DE∥BC,∴==,∴===,∵DE∥BC,∴△ADE∽△ABC,∴=()2=,∴=,即= (2)∵AB=4,AD=m,∴BD=4-m,∵DE∥BC,∴==,∴==,∵DE∥BC,∴△ADE∽△ABC,∴=()2=,∴=·=·=,即= 问题2:如图②,分别延长BA,CD交于点O,∵AD∥BC,∴△OAD∽△OBC,∴==,∴OA=AB=4,∴OB=8,∵AE=n,∴OE=4+n,∵EF∥BC,由问题1的解法可知:=·=×()2=,∵=()2=,∴=,∴==×=,即=
6
相关文档
- 九年级数学上册第23章图形的相似232021-11-114页
- 九年级数学上册第23章图形的相似232021-11-113页
- 九年级数学上册第四章图形的相似62021-11-113页
- 九年级数学上册第四章图形的相似12021-11-112页
- 九年级数学上册第23章图形的相似232021-11-113页
- 九年级数学上册第四章图形的相似阶2021-11-1121页
- 华师版九年级上册数学同步练习课件2021-11-1110页
- 北师大版数学九年级上册同步练习课2021-11-1129页
- 北师大版数学九年级上册同步练习课2021-11-1132页
- 九年级数学上册第23章图形的相似232021-11-103页