九年级数学上册第一章特殊平行四边形专题课堂二特殊平行四边形中的折叠问题课件新版北师大版 21页

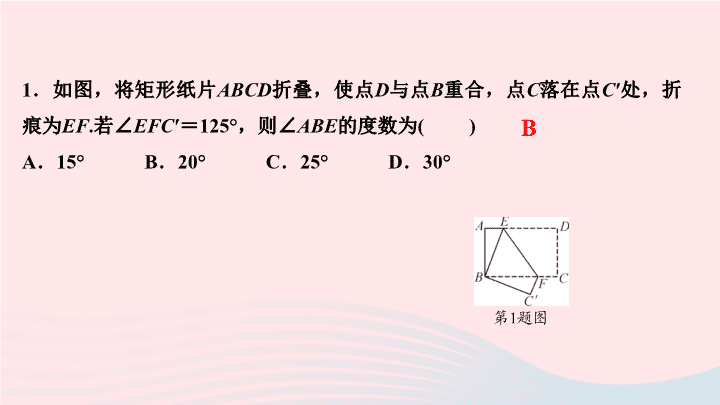
第一章　特殊平行四边形 专题课堂(二)　特殊平行四边形中的折叠问题 1 ．如图，将矩形纸片 ABCD 折叠，使点 D 与点 B 重合，点 C 落在点 C ′ 处，折痕为 EF . 若∠ EFC ′ ＝ 125° ，则∠ ABE 的度数为 ( ) A ． 15° 　　　 B ． 20° 　　　 C ． 25° 　　　 D ． 30° B 2 ．如图，将正方形纸片 ABCD 折叠，使边 AB ， CB 均落在对角线 BD 上，得折痕 BE ， BF ，则∠ EBF 的大小为 ( ) A ． 15° B ． 30° C ． 45° D ． 60° C 3 ．如图，在菱形 ABCD 中，∠ A ＝ 120° ， E 是 AD 上的点，沿 BE 折叠△ ABE ，点 A 恰好落在 BD 上的点 F 处，连接 CF ，那么∠ BFC 的度数是 ( ) A ． 60° B ． 70° C ． 75° D ． 80° C 4 ．如图，矩形 ABCD 沿直线 EF 对折，点 D 恰好与 BC 边上的点 H 重合，∠ GFP ＝ 62° ，那么∠ EHF 的度数等于 ___________ ． 56° 5 ．如图，将矩形纸片 ABCD 折叠，使边 AB ， BC 均落在对角线 BD 上，得到折痕 BE ， BF ，求∠ EBF 的度数． 解：∠ EBF 的度数为 45° A B 9 ．如图，正方形纸片 ABCD 的边长 AB ＝ 12 ， E 是 DC 上一点， CE ＝ 5 ，折叠正方形纸片使点 B 和点 E 重合，折痕为 FG ，则 FG 的长为 ______ ． 13 10 ．如图，将一张菱形纸片 ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形 EFGH . 若 EF ＝ 4 ， EH ＝ 3 ，则 AB ＝ ____ ． 5 解： (1) 由折叠及矩形的性质可知 EG ＝ AE ＝ A ′ E ＝ AD ， CH ＝ BC ＝ AD ，∴ EG ＝ CH 12 ．如图，在矩形 ABCD 中， AB ＝ 8 ， BC ＝ 4 ，将矩形的一角沿 AC 折叠，则重叠阴影部分△ AFC 的面积为 ( ) A ． 14 B ． 12 C ． 10 D ． 8 C D 14 ．如图，将一矩形纸片 ABCD 折叠，使两个顶点 A ， C 重合，折痕为 FG . 若 AB ＝ 4 ， BC ＝ 8 ，则△ ABF 的面积为 ____ ． 6 15 ． ( 济宁中考 ) 实验探究： (1) 如图①，对折矩形纸片 ABCD ，使 AD 与 BC 重合，得到折痕 EF ，把纸片展开；再一次折叠纸片，使点 A 落在 EF 上，并使折叠经过点 B ，得到折痕 BM ，同时得到线段 BN ， MN . 请你观察图①，猜想∠ MBN 的度数是多少，并证明你的结论； (2) 将图①中的三角形纸片 BMN 剪下，如图② . 折叠该纸片，探究 MN 与 BM 的数量关系，写出折叠方案，并结合方案证明你的结论．