- 92.50 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第3课时 矩形的性质与判定的应用
1.能够运用矩形的性质定理和判定定理解决问题.
2.经历矩形的性质与判定的应用过程,发展学生的推理论证能力.
3.通过学生独立完成证明的过程,让学生体会数学的严谨性.
重点
矩形的性质定理与判定定理的应用.
难点
灵活地运用矩形的性质定理与判定定理解决问题.
一、复习导入
1.如图①,矩形ABCD的两条对角线相交于点O,已知∠AOD= 120°,AB=2.5 cm,则∠DAO=__________,AC=__________ cm,S矩形ABCD=__________ cm2.
2. 如图②,四边形ABCD是平行四边形,添加一个条件________________,可使它成为矩形.
二、探究新知
课件出示:如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE.求AE的长.
学生小组合作完成本题的求解,教师点评并板书:
解:∵ 四边形ABCD是矩形,
∴AO=BO=DO=BD(矩形的对角线相等且互相平分),
∠BAD=90°(矩形的四个角都是直角).
∵ED=3BE,
∴BE=OE.
又∵ AE⊥BD,
∴AB=AO.
∴AB=AO=BO.
即 △ABO是等边三角形.
∴∠ABO=60°.
∴∠ADB=90°-∠ABO=30°.
4
在Rt△AED中,
∵∠ADE=30°,
∴AE=AD=×6=3.
注意:本题的解法不唯一,采取小组合作时,应当鼓励学生提出自己不同的意见.
三、举例分析
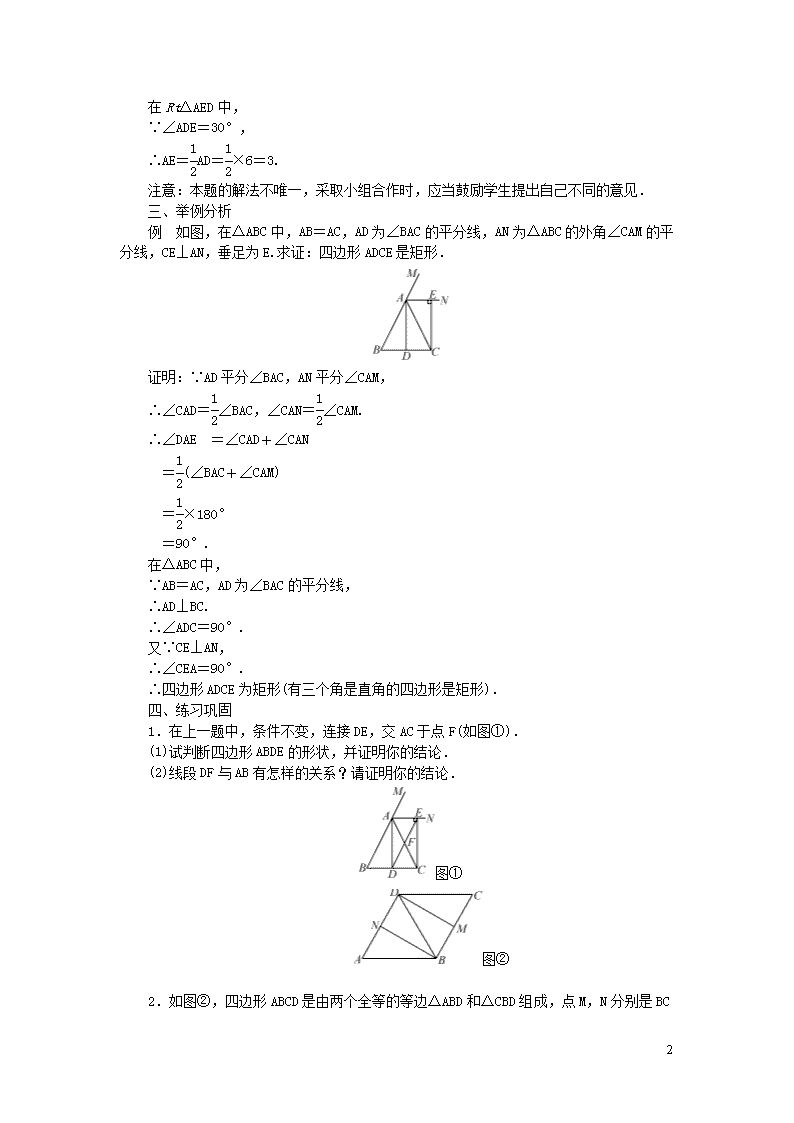
例 如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD=∠BAC,∠CAN=∠CAM.
∴∠DAE =∠CAD+∠CAN
=(∠BAC+∠CAM)
=×180°
=90°.
在△ABC中,
∵AB=AC,AD为∠BAC的平分线,
∴AD⊥BC.
∴∠ADC=90°.
又∵CE⊥AN,
∴∠CEA=90°.
∴四边形ADCE为矩形(有三个角是直角的四边形是矩形).
四、练习巩固
1.在上一题中,条件不变,连接DE,交AC于点F(如图①).
(1)试判断四边形ABDE的形状,并证明你的结论.
(2)线段DF与AB有怎样的关系?请证明你的结论.
图①
图②
2.如图②,四边形ABCD是由两个全等的等边△ABD和△CBD组成,点M,N
4
分别是BC和AD的中点.求证:四边形BMDN是矩形.
五、小结
通过本节课的学习,你有什么收获?还有哪些疑问?
六、课外作业
教材第18~19页习题1.6第1~5题.
本课时,是综合运用矩形的性质定理和判定定理,应给予学生充分的时间和空间展示自己,不仅有利于提高学生学习的积极性,更有利于教师发现学生的独到见解和新思维、新想法,同时还能发现学生存在的问题,这对于课堂教学是非常有利的.在教学过程中,不应加大习题量,题目在精不在多,扎实地讲解和学习比大量练习要有效果得多.把关注学生能力的培养提到首位,达到本节课所要完成的真正目标.
4
4