中考数学专题复习练习：线段的中垂线 12页

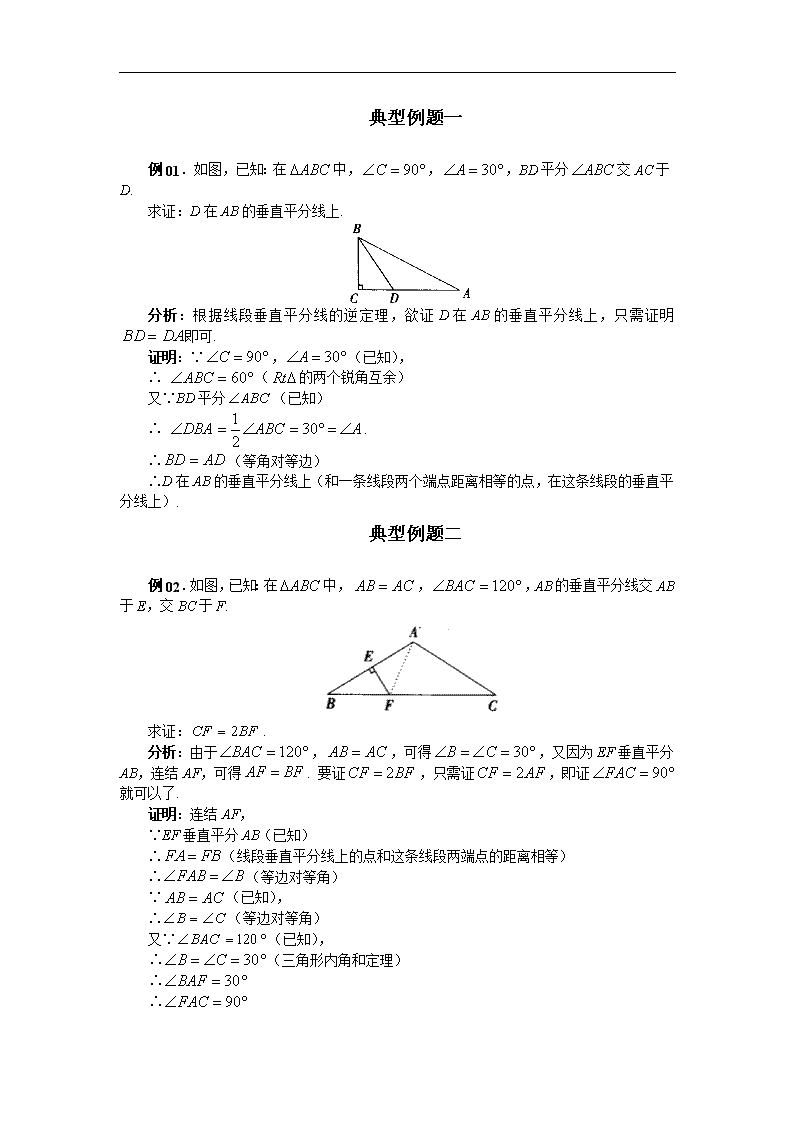
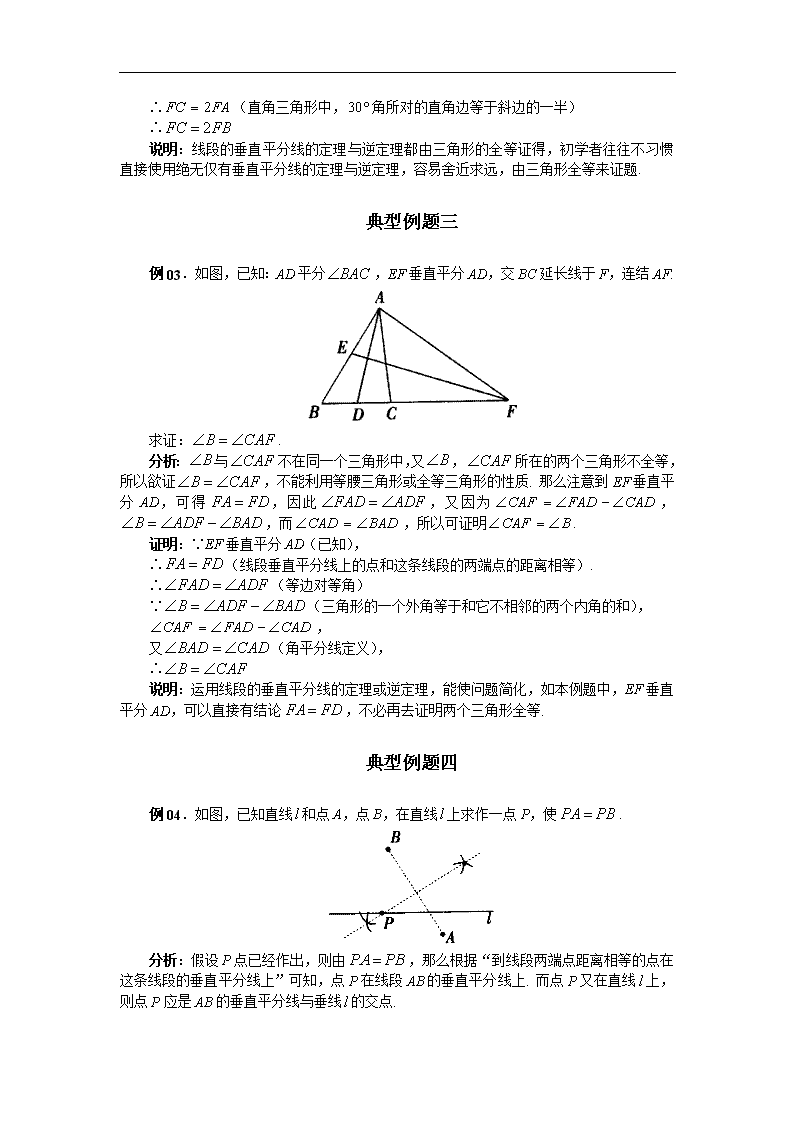
典型例题一 例01．如图，已知：在中，，，BD平分交AC于D.‎ 求证：D在AB的垂直平分线上. ‎ 分析：根据线段垂直平分线的逆定理，欲证D在AB的垂直平分线上，只需证明即可. ‎ 证明：∵，（已知），‎ ‎∴ （的两个锐角互余）‎ 又∵BD平分（已知）‎ ‎∴ . ‎ ‎∴（等角对等边）‎ ‎∴D在AB的垂直平分线上（和一条线段两个端点距离相等的点，在这条线段的垂直平分线上）.‎ 典型例题二 例02．如图，已知：在中，，，AB的垂直平分线交AB于E，交BC于F. ‎ 求证：. ‎ 分析：由于，，可得，又因为EF垂直平分AB，连结AF，可得. 要证，只需证，即证就可以了. ‎ 证明：连结AF，‎ ‎∵EF垂直平分AB（已知）‎ ‎∴（线段垂直平分线上的点和这条线段两端点的距离相等）‎ ‎∴（等边对等角）‎ ‎∵（已知）， ‎ ‎∴（等边对等角）‎ 又∵（已知），‎ ‎∴（三角形内角和定理）‎ ‎∴ ‎ ‎∴‎ ‎∴（直角三角形中，角所对的直角边等于斜边的一半）‎ ‎∴‎ 说明：线段的垂直平分线的定理与逆定理都由三角形的全等证得，初学者往往不习惯直接使用绝无仅有垂直平分线的定理与逆定理，容易舍近求远，由三角形全等来证题. ‎ 典型例题三 例03．如图，已知：AD平分，EF垂直平分AD，交BC延长线于F，连结AF. ‎ 求证：. ‎ 分析：与不在同一个三角形中，又，所在的两个三角形不全等，所以欲证，不能利用等腰三角形或全等三角形的性质. 那么注意到EF垂直平分AD，可得，因此，又因为，，而，所以可证明. ‎ 证明：∵EF垂直平分AD（已知），‎ ‎∴（线段垂直平分线上的点和这条线段的两端点的距离相等）. ‎ ‎∴（等边对等角）‎ ‎∵（三角形的一个外角等于和它不相邻的两个内角的和），‎ ‎，‎ 又（角平分线定义），‎ ‎∴‎ 说明：运用线段的垂直平分线的定理或逆定理，能使问题简化，如本例题中，EF垂直平分AD，可以直接有结论，不必再去证明两个三角形全等. ‎ 典型例题四 例04．如图，已知直线和点A，点B，在直线上求作一点P，使. ‎ 分析：假设P点已经作出，则由，那么根据“到线段两端点距离相等的点在这条线段的垂直平分线上”可知，点P在线段AB的垂直平分线上. 而点P又在直线上，则点P应是AB的垂直平分线与垂线的交点. ‎ 作法：1．连结AB. ‎ ‎2．作线段AB的垂直平分线，交直线于点P. ‎ 则P即为所求的点. ‎ 说明：在求作一个点时，要考虑该点具备什么样的特点，如它到一条线段的两个端点距离相等，它就在连结这两点的线段的垂直平分线上，如果它到一个角的两边的距离相等，它就在这个角的平分线上. ‎ 典型例题五 例05．如图所示，在，，DE垂直平分AB，交AB于E，交BC于D，，求的度数. ‎ 分析：由于DE垂直平分AB，所以，又为直角三角形，由直角三角形中两锐角互余，即可求出的度数. ‎ 解答：∵DE垂直平分AB，‎ ‎∴ ‎ ‎∴ ，‎ 在中，，‎ ‎∴ ，‎ 而，‎ ‎，，‎ ‎∴，‎ ‎∴，∴‎ 答：的度数为. ‎ 典型例题六 例06．求证：三角形两边中垂线的交点在第三边的中垂线上. ‎ 分析：文字题应先根据题意画出图形，并根据图形写出已知、求证.‎ 已知：中，（如图），EF、MN分别为AB、BC边的中垂线且交于O. ‎ 求证：点O在AC的中垂线上. ‎ 证明：连结OA、OB、OC ‎∵ EF为AB的中垂线 ‎∴ ‎ 同理得： ∴‎ ‎∴点O在AC的中垂线上 典型例题七 例07．如图所示，，. ‎ 求证：. ‎ 分析：要证，只需证直线AB是线段CD的垂直平分线即可. ‎ 证明：连结CD，延长AB交CD于E. ‎ ‎∵ ，‎ ‎∴ 为等腰三角形，‎ ‎∵ ，‎ ‎∴ ，‎ ‎∴ BE是等腰的角平分线，‎ ‎∴BE垂直平分CD（等腰三角形顶角平分线平分且垂直底边），‎ ‎∴直线AE是线段CD的垂直平分线，‎ 又∵点A在直线AE上，‎ ‎∴（线段垂直平分线上的点到这条线段两端点的距离相等）‎ 说明 本例也可以通过证明，得出，利用线段垂直平分线的性质定理和逆定理为我们证明线段（或角）相等又提供了一个新的方法. ‎ 典型例题八 例08．如图所示：已知内有两点A、B，在内部找到一点D，使得D点到A、B两点的距离相等，并且点D到的两边也相等. ‎ 分析：欲使点D到A、B两点的距离相等，由线段的垂直平分线的判定定理可知，点D一定在AB的垂直平分线上；D点又要满足到的两边距离相等，由平分线的判定定理可知点D一定在的平分线上，综合以上两点，可以推知点D是线段AB的垂直平分线与的平分线的交点，因此可以据此找到D点. ‎ 作法：（1）连结AB，作AB的垂直平分线MN. ‎ ‎（2）作的角平分线OP，与MN相交于一点D. ‎ ‎ 则D点就是满足要求的点. ‎ 选择题 ‎1．选择题 ‎（1）如图，已知：，那么（ ）‎ ‎（A）CD垂直平分AB （B）AB垂直平分CD ‎（C）CD与AB互相垂直平分 （D）以上说法都正确 ‎（2）如果三角形三边的垂直平分线的交点正好在三角形的一条边上，那么这个三角形是（ ）‎ ‎（A）直角三角形 （B）锐角三角形 ‎（C）钝角三角形 （D）以上都有可能 参考答案：‎ ‎1．选择题 ‎（1）B （2）A 填空题 ‎1．填空题 ‎（1）和线段两个端点距离相等的点的集合是________. ‎ ‎（2）在中，，AD为角平分线，则有AD______BC（填或），_____. 如果E为AD上的一点，那么_______. 如果，，那么点D到AD的距离是______. ‎ ‎（3）已知：在中，，，DE垂直平分AB，且交CA的延长线于D，则的度数为_______. ‎ ‎（4）在等腰三角形ABC中，，腰AB的垂直平分线交另一腰AC于D，若的周长为，则底边BC的长为______. ‎ ‎（5）如图，在中，，BC的垂直平分线交AB于D，垂足为E. ‎ ‎①若，则______，________. ‎ ‎②若，，则的周长为______. ‎ ‎（6）如图，在中，，AB的垂直平分线交AB于D，交AC于E，，的周长为12，则_____. ‎ ‎（7）如图，在中，，，DE是AB的垂直平分线，则_______. ‎ ‎（8）如图，在中，AC的垂直平分线交AC于E，交BC于D，的周长为，，则的周长为_______. ‎ ‎（9）如图，已知在直角三角形ABC中，，，DE垂直平分AB ‎，交BC于E，，则______. ‎ ‎（10）在中，，，AC的垂直平分线交BC于D，交AC于E，若，则BC的长度为______. ‎ 参考答案：‎ ‎1．填空题 ‎（1）线段的垂直平分线 （2），CD，EC，2 （3） （4） ‎ ‎（5）①， ②15 （6）4 （7） （8）17 （9） （10）30‎ 解答题 ‎1．作图题 ‎（1）已知：如图，B为的边OB上的一点，‎ 求作：点P，使P点到OA和OB的距离相等，并且有. ‎ ‎（2）已知不在同一直线上的三点A、B、C，求作一点P，使. ‎ 参考答案：‎ ‎1．作图题 ‎（1）作法：①画出的平分线OC，‎ ‎②作出OB的垂直平分线MN，则OC与MN的交点即为所要求的点P. ‎ ‎（2）①作线段AB的垂直平分线MN，‎ ‎②作线段BC的垂直平分线CD. 则AB与CD的交点即为所要求的点P. ‎ 解答题 ‎1．计算题 ‎（1）如图，已知：在直角三角形ABC中，，E为AB的中点，且交BC于D，连结AD，若，求：和的度数. ‎ ‎（2）如图，已知：在中，，BC边上的垂直平分线交AC于D，交BC于E. BD分为两部分，若. 求的度数. ‎ ‎（3）如图，已知：在中，，MP和NQ分别是AB和AC的垂直平分线，求的大小. ‎ 参考答案：‎ ‎1．计算题 ‎（1）解：E为AB中点，且，∴DE为AB的垂直平分线，‎ ‎∴，∴. 又，∴，‎ ‎∵，∴，‎ 即，求得，∴. ‎ ‎（2）解：DE为BC的垂直平分线，∴，‎ 又∵，∴. ‎ ‎∵，∴，‎ 即，求得. ‎ ‎（3）解：PM与QN为AB与AC的垂直平分线，‎ ‎∴. ∴，. ‎ 又∵ ，‎ ‎∴‎ 解答题 ‎1．证明题 ‎（1）如图，已知：，DE是AB的垂直平分线，D为垂足，交BC于E，. 求证：. ‎ ‎（2）如图，已知：线段CD垂直平分AB，AB平分. 求证：. ‎ ‎（3）如图，已知：AD是的高，E为AD上一点，且. ‎ 求证：是等腰三角形. ‎ ‎（4）如图，已知：在中，，DE垂直平分线AC交AB于D，交AC于E. 求证：. ‎ ‎（5）如图，已知：E是的平分线上的一点，，，垂足分别是C、D. 求证：OE垂直平分CD. ‎ ‎（6）如图，已知：在中，AB、BC边上的垂直平分线相交于点P. ‎ 求证：点P在AC的垂直平分线上. ‎ ‎（7）如图，已知：AD是的的平分线，AD的垂直平分线EF，交BC的延长线于F，交AD于E，求证：. ‎ ‎（8）如图，已知：在中，的平分线交BC于D，且，，垂足分别是E、F. 求证：AD是EF的垂直平分线. ‎ ‎（9）如图，已知：，，，，. 求证：. ‎ 参考答案 ‎1．证明题 ‎（1）证明：连结AE，由于，，∴，，∵DE是AB的垂直平分线，∴，∴，∴，即AE是的角平分线，∴. ‎ ‎（2）证明：∵CD是AB的垂直平分线，∴，∴，又∵，∴，∴.‎ ‎（3）证明：∵，∴AD是BC的垂直平分线，∴，∴是等腰三角形. ‎ ‎（4）证明：DE垂直平分AC，∴，∴，∵，又有，∴，∴. ‎ ‎（5）证明：OE是的平分线，∴，∴，∴，∴O与E都在CD的垂直平分线上，∴OE垂直平分CD. ‎ ‎（6）证明：P是AB、BC边上的垂直平分线，∴，∴，∴P点在AC的垂直平分线上. ‎ ‎（7）证明：EF垂直平分AD，∴，∴. ‎ ‎∴‎ ‎（8）证明：∵AD是的平分线，且，，∴，∴易证，∴，∴A与D都在EF的垂直平分线上，∴AD就是EF的垂直平分线. ‎ ‎（9）证明：，且，∴. 又∵，∴，∴，∴AC为DM的垂直平分线，∴，∴. ‎ 能力训练 ‎1、若一个三角形两边的垂直平分线的交点在第三边上，则这个三角形是（　　）‎ A、锐角三角形　 B、钝角三角形 C、直角三角形 D、不能确定 答：C　提示：此交点恰好为斜边的中点 ‎2、如图，∠BAC=，若MP、NQ分别垂直平分AB、AC，则∠PAQ的度数＿＿＿＿‎ A B C M N P Q 提示：利用三角形内角和求得∠B+∠C＝，‎ 再转化为∠BAP+∠CAQ＝‎ A B C D E ‎3、如图，△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为12，AC＝5，则△ABC的周长＝＿＿＿＿‎ 提示：把DC转化为AD，利用△ABD的周长. 答：17‎ ‎4、如图，△ABC中∠A＝，∠C＝，AC＝12，DE垂直平分BC，‎ 则BE＝＿＿＿‎ 答：24‎ A B C P M N ‎5、如图，已知：△ABC中，AB、BC边上的垂直平分线相交于点P. ‎ 求证：点P在AC的垂直平分线上 证明：连结PA、PB、PC ‎∵PM垂直平分AB，PN垂直平分BC ‎∴PA＝PB，PB＝PC ‎∴PA＝PC ‎∴点P在AC的垂直平分线上 C D A B E F ‎6、如图，△ABC中，AD为∠A的平分线，FE垂直平分AD，E为垂足，交BC的延长线于F.‎ 求证：∠B＝∠CAF 证明：‎ ‎∵EF垂直平分AD ‎∴∠ADF＝∠DAF，∠ADF＝∠B+∠BAD ‎∵∠BAD＝∠CAD，‎ ‎∴∠ADC＝∠B+∠CAD ，‎ 又∵∠DAF＝∠CAD+∠CAF ‎∴∠B＝∠CAF