江西专版2020中考数学复习方案第四单元图形的初步认识与三角形第20课时锐角三角函数及其应用课件 49页

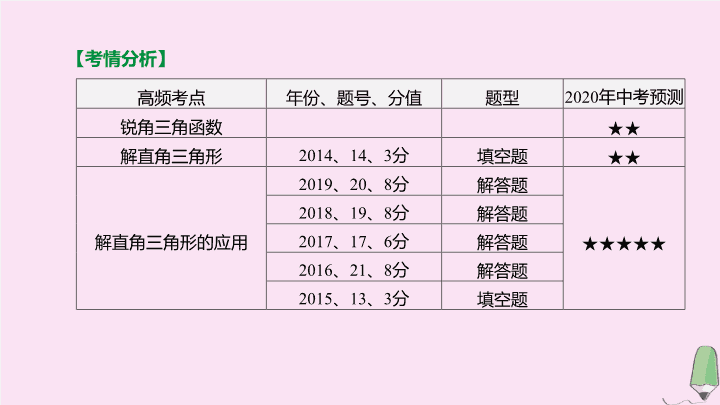
第 20 课时 锐角三角函数及其应用 第四单元　图形的初步认识与三角形 【考情分析】 高频考点 年份、题号、分值 题型 2020年中考预测 锐角三角函数 ★★ 解直角三角形 2014、14、3分 填空题 ★★ 解直角三角形的应用 2019、20、8分 解答题 ★★★★★ 2018、19、8分 解答题 2017、17、6分 解答题 2016、21、8分 解答题 2015、13、3分 填空题 基 础 知 识 巩 固 高 频 考 向 探 究 考点一　锐角三角函数 考点聚焦 图20-1 基 础 知 识 巩 固 高 频 考 向 探 究 考点二　特殊角的三角函数值 基 础 知 识 巩 固 高 频 考 向 探 究 90 考点三　解直角三角形 c2 图20-2 基 础 知 识 巩 固 高 频 考 向 探 究 1.仰角和俯角 　　如图20-3,在视线与水平线所成的角中,视线在水平线⑪ 　　　　的角叫仰 角;视线在水平线⑫ 　　　　的角叫俯角. 下方 考点四　解直角三角形的应用 上方 图20-3 基 础 知 识 巩 固 高 频 考 向 探 究 图20-4 坡度(或坡比) 坡角 陡 基 础 知 识 巩 固 高 频 考 向 探 究 3.方向角 (1)指南或指北方向线与目标方向线所成的小于90°的角叫做方向角. (2)方向角的识别,关键是看该角由哪个主方向向次方向偏离,偏离多少度,则读作 主方向偏离次方向多少度.如图20-5,由北向东偏30°读作⑯ 　    　　　,由南向 东偏50°读作⑰ 　　      　　,西南方向是指⑱ 　　       　　.  北偏东30° 图20-5 南偏东50° 南偏西45° 基 础 知 识 巩 固 高 频 考 向 探 究 题组一　必会题 对点演练 A 基 础 知 识 巩 固 高 频 考 向 探 究 图20-6 D 基 础 知 识 巩 固 高 频 考 向 探 究 图20-7 基 础 知 识 巩 固 高 频 考 向 探 究 [答案]C 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 图20-8 [答案]2 基 础 知 识 巩 固 高 频 考 向 探 究 图20-9 6.[2019·德州]如图20-9,一架长为6米的梯子AB斜靠 在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子 的底端B外移到D,那么梯子顶端A下移到C,这时又 测得∠CDO=50°,那么AC的长度约为　　　　米.  (sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64) [答案] 1.02 基 础 知 识 巩 固 高 频 考 向 探 究 题组二　易错题 【失分点】 构造不了直角三角形;解直角三角形构图时忽视高的多种情况. 图20-10 [答案]B 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 考向一　解直角三角形 图20-11 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】(1)运用锐角三角函数解决某些问题时,通常都是在直角三角形中 进行,若没有直角三角形,常通过添加垂线段(改斜为直)、平行线等方法构建直 角三角形. (2)若所给条件与所求结论之间不具备直接的关系,往往需要通过“中间角”或“中 间线段”进行“搭桥”与“转化”,因此“搭桥”“转化”与“构造”是解决直角三角形问 题的法宝与关键. 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图20-12 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 考向二　解直角三角形的实际应用 例2[2019·江西20题]图20-13①是一台实物投影仪,图②是它的示意图,折线B— A—O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕 点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD =8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1 cm) (1)如图②,∠ABC=70°,BC∥OE. ①填空:∠BAO=　　　　°; ②求投影探头的端点D到桌面OE的距离. 图20-13 基 础 知 识 巩 固 高 频 考 向 探 究 (2)如图③,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm 时,求∠ABC的大小. (参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60) 图20-13 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 例2[2019·江西20题]图20-13①是一台实物投影仪,图②是它的示意图,折线B— A—O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕 点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8 cm,CD =8 cm,AB=30 cm,BC=35 cm.(结果精确到0.1 cm) (2)如图③,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6 cm 时,求∠ABC的大小.(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60, cos53.2°≈0.60) 图20-13 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】求解此类问题,一般是先构造直角三角形,利用三角函数或相似三 角形来解决问题.常见的基本图形有如下几种: ①不同地点看同一点(如图20-14); ②同一地点看不同点(如图20-15); ③利用反射构造相似(如图20-16); ④堤坝问题(如图20-17). 图20-14 图20-15 图20-16 图20-17 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图20-18 角度1　直角三角形模型 1.[2017·江西17题]研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约 为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.如图20-18是其侧面 简化示意图,其中视线AB水平,且与屏幕BC垂直. (1)若屏幕上下宽BC=20 cm,科学使用电脑时, 求眼睛与屏幕的最短距离AB的长. 基 础 知 识 巩 固 高 频 考 向 探 究 (2)若肩膀到水平地面的距离DG=100 cm,上臂DE=30 cm,下臂EF水平放置在键 盘上,其到地面的距离FH=72 cm.请判断此时β是否符合科学要求的100°. 图20-18 基 础 知 识 巩 固 高 频 考 向 探 究 1.[2017·江西17题]研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约 为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.如图20-18是其侧面 简化示意图,其中视线AB水平,且与屏幕BC垂直. (2)若肩膀到水平地面的距离DG=100 cm,上臂DE=30 cm,下臂EF水平放置在键 盘上,其到地面的距离FH=72 cm.请判断此时β是否符合科学要求的100°. 图20-18 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2018·江西19题]图20-19①是一种折叠门,由上下轨道和两扇长宽相等的活页 门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图②是其俯 视简化示意图,已知轨道AB=120 cm,两扇活页门的宽OC=OB=60 cm,点B固定,当 点C在AB上左右运动时,OC与OB的长度不变.(所有结果保留小数点后一位) (1)若∠OBC=50°,求AC的长; (2)当点C从点A向右运动60 cm时, 求点O在此过程中运动的路径长. 参考数据:sin50°≈0.77,cos50°≈0.64, tan50°≈1.19,π取3.14. 图20-19 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2018·江西19题]图20-19①是一种折叠门,由上下轨道和两扇长宽相等的活页 门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图②是其俯 视简化示意图,已知轨道AB=120 cm,两扇活页门的宽OC=OB=60 cm,点B固定,当 点C在AB上左右运动时,OC与OB的长度不变.(所有结果保留小数点后一位) (2)当点C从点A向右运动60 cm时, 求点O在此过程中运动的路径长. 参考数据:sin50°≈0.77,cos50°≈0.64, tan50°≈1.19,π取3.14. 图20-19 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 角度2　圆模型 3.[2013·江西21题]一辆汽车的背面有一种特殊形状的刮雨器,忽略刮雨器的宽 度可抽象为一条折线OAB,如图20-20①所示,量得连杆OA长为10 cm,雨刮杆AB 长为48 cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位 置,如图20-20②所示. (1)求雨刮杆AB旋转的最大角度及O,B两点之间 的距离;(结果精确到0.01) (2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍) 图20-20 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 3.[2013·江西21题]一辆汽车的背面有一种特殊形状的刮雨器,忽略刮雨器的宽 度可抽象为一条折线OAB,如图20-20①所示,量得连杆OA长为10 cm,雨刮杆AB 长为48 cm,∠OAB=120°.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位 置,如图20-20②所示. (2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍) 图20-20 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 角度3　特殊四边形模型 4.[2014·江西21题]中国结挂件是由四个相同的菱形在顶点处依次串接而成,每 相邻两个菱形均成30°的夹角,示意图如图20-21所示,每个菱形的边长为10 cm, 锐角为60°. (1)连接CD,EB,猜想它们的位置关系并加以证明; (2)求A,B两点之间的距离.(结果取整数,可以使用计算器) 图20-21 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 4.[2014·江西21题]中国结挂件是由四个相同的菱形在顶点处依次串接而成,每 相邻两个菱形均成30°的夹角,示意图如图20-21所示,每个菱形的边长为10 cm, 锐角为60°. (2)求A,B两点之间的距离.(结果取整数,可以使用计算器) 图20-21 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究