江西专版2020中考数学复习方案第五单元四边形第22课时矩形课件 42页

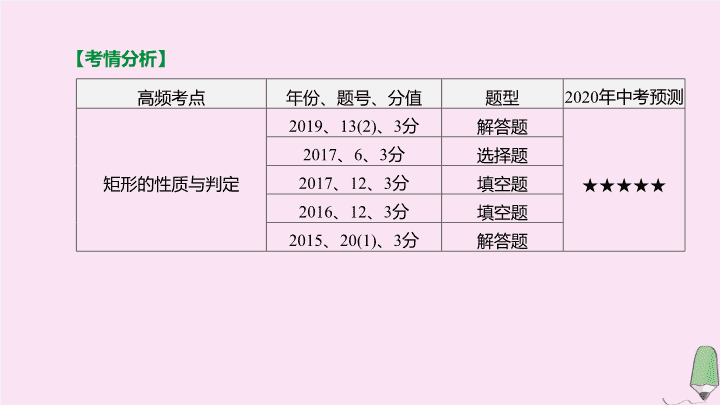
第 22 课时 矩形 第五单元　四边形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 矩形的 性质 与判定 2019 、 13(2) 、 3 分 解答题 ★★★★★ 2017 、 6 、 3 分 选择题 2017 、 12 、 3 分 填空题 2016 、 12 、 3 分 填空题 2015 、 20(1) 、 3 分 解答题 定义 　 有一个角是直角的平行四边形叫做矩形 . 性质 (1) 边 : 对边平行 , 对边相等 ; (2) 角 : 四个角都是 ① 　　　　 ;  (3) 对角线 : 对角线 ② 　 　　　 ;  (4) 对称性 : 既是 ③ 　　　 对称图形 , 又是 ④ 　　　　 对称图形 , 有 ⑤ 　　　　 条对称轴   考点　矩形 考点聚焦 直角 相等且互相平分 中心 轴 2 判定 (1) 有一个角是 ⑥ 　　　　 的平行四边形是矩形 ( 定义 );  (2) 有 ⑦ 　　　　 是直角的四边形是矩形 ;  (3) 对角线 ⑧ 　　　　 的平行四边形是矩形   周长、 面积 C= 2( a + b ), S=ab ( a , b 分别为矩形的长和宽 ) 拓展 矩形的两条对角线把矩形分成四个面积相等的等腰三角形 ( 续表 ) 直角 三个角 相等 题组一　必会题 对点演练 1 . [2019· 无锡 ] 下列结论 , 矩形具有而菱形不一定具有的性质是 ( 　　 ) A . 内角和为 360° B . 对角线互相平分 C . 对角线相等 D . 对角线互相垂直 C 2 . 下列命题错误的是 ( 　　 ) A . 有一个角是直角的平行四边形是矩形 B . 对角线相等的四边形是矩形 C . 有三个角是直角的四边形是矩形 D . 对角线互相平分且相等的四边形是矩形 B 3 . [2019· 九江二模 ] 如图 22-1, 把一张矩形纸片 ABCD 沿 EF 折叠后 , 点 A 落在 CD 边上的点 A' 处 , 点 B 落在点 B' 处 , 若∠ 2 = 40°, 则图中∠ 1 的度数为 ( 　　 ) A . 115° B . 120° C . 130° D . 140° 图 22-1 [ 答案 ] A 　 [ 解析 ] 由折叠知∠ BFE= ∠ EFB' , ∠ B'= ∠ B= 90° . ∵∠ 2 = 40°, ∴∠ CFB'= 50°, ∴∠ 1+ ∠ EFB' - ∠ CFB'= 180°, 即∠ 1+ ∠ 1-50° = 180°, 解得∠ 1 = 115° . 故选 A . 4 . [2019· 江西样卷五 ] 如图 22-2 所示为一种古代界尺 , 主要用于界画绘制时作平行线 . 该界尺由四根等宽的木条连接而成 , 设外框为矩形 ABCD , 内框为矩形 EFGH. 测得 EF= 15 cm, AB= 21 cm, AD= 40 cm, 则 FG 的长为 　　　　 cm .  图 22-2 34 5 . 如图 22-3, 矩形 ABCD 的两条对角线相交于点 O , ∠ AOB= 60°, AB= 2, 则矩形的对角线 AC 的长是 　　　　 .  图 22-3 4 6 . [2019· 江西样卷七 ] 如图 22-4, 在矩形 ABCD 中 , 对角线 AC , BD 相交于点 O , 点 E , F 分别是 AO , AD 的中点 . 若 AD= 8 cm, AC= 10 cm, 则 △ AEF 的周长为 　　　　 cm .  图 22-4 9 题组二　易错题 【 失分点 】 运用矩形的性质时 , 由于对性质理解不清造成解题错误 ; 不能正确画出图形导致解答不全面 . 图 22-5 [ 答案 ] A 8 . 已知矩形 ABCD 的对角线相交于点 O , AE 平分∠ BAD 交矩形的边于点 E , 若∠ CAE= 10°, 则∠ AOB 的度数为 　　　　 .  [ 答案 ] 70° 或 110° 　 [ 解析 ] 根据题意画出如下示意图 : ∵四边形 ABCD 是矩形 , ∴∠ BAD= 90°, OA=OB=OD. ∵ AE 平分∠ BAD , ∴∠ BAE= ∠ DAE= 45° . ∵∠ CAE= 10°, 由图①得 , ∠ BAO= ∠ BAE + ∠ EAC= 45°+10° = 55° . 又∵ OA=OB , ∴∠ BAO= ∠ OBA= 55°, ∴∠ AOB= 180°-55°-55° = 70° . 由图②得 , ∠ DAO= ∠ DAE + ∠ EAC= 45°+10° = 55° . 又∵ OA=OD , ∴∠ OAD= ∠ ODA= 55°, ∴∠ AOB= ∠ OAD + ∠ ODA= 110° . 综上所述 : ∠ AOB 的度数为 70° 或 110° . 考向一　矩形的性质及判定 图 22-6 解 :(1) 证明 : ∵四边形 ABCD 是平行四边形 , ∴ AD ∥ BC , DC ∥ AB , ∴∠ CDB= ∠ ABD. ∵ BE 平分∠ ABD , DF 平分∠ CDB , ∴∠ FDB= ∠ EBD , ∴ DF ∥ BE. 又 AD ∥ BC , ∴四边形 DFBE 是平行四边形 . 又∵∠ DEB= 90°, ∴四边形 DFBE 是矩形 . 图 22-6 (2) 证明 : 由 (1) 可得四边形 DFBE 是平行四边形 , ∵ BE 平分∠ ABD , 且 AB=BD , ∴ BE ⊥ AD , ∴四边形 DFBE 是矩形 . 图 22-6 【 方法点析 】 证明一个四边形为矩形可以直接证明三个角等于 90 °; 或者先说明是平行四边形再说明有一个角是 90 °; 或证明对角线相等且平分 . | 考向精练 | 图 22-7 2 . [2018· 江西 10 题 ] 如图 22-8, 在矩形 ABCD 中 , AD= 3, 将矩形 ABCD 绕点 A 逆时针旋转 , 得到矩形 AEFG , 点 B 的对应点 E 落在 CD 上 , 且 DE=EF , 则 AB 的长为 　　　　 .  图 22-8 3 . [2019· 江西 13(2) 题 ] 如图 22-9, 四边形 ABCD 中 , AB=CD , AD=BC , 对角线 AC , BD 相交于点 O , 且 OA=OD. 求证 : 四边形 ABCD 是矩形 . 图 22-9 证明 : ∵ AB=CD , AD=BC , ∴四边形 ABCD 是平行四边形 , ∴ AC , BD 互相平分 . 又∵ OA=OD , ∴ AC=BD , ∴四边形 ABCD 是矩形 . 4 . [2019· 北京朝阳二模 ] 如图 22-10, 在 ▱ ABCD 中 , ∠ ABD= 90°, 延长 AB 至点 E , 使 BE=AB , 连接 CE. (1) 求证 : 四边形 BECD 是矩形 ; (2) 连接 DE 交 BC 于点 F , 连接 AF , 若 CE= 2, ∠ DAB= 30°, 求 AF 的长 . 图 22-10 解 :(1) 证明 : ∵四边形 ABCD 是平行四边形 , ∴ CD=AB , CD ∥ AB. ∵ BE=AB , ∴ BE=CD. ∴四边形 BECD 是平行四边形 . ∵∠ ABD= 90°, ∴∠ DBE= 90° . ∴ ▱ BECD 是矩形 . 4 . [2019· 北京朝阳二模 ] 如图 22-10, 在 ▱ ABCD 中 , ∠ ABD= 90°, 延长 AB 至点 E , 使 BE=AB , 连接 CE. (2) 连接 DE 交 BC 于点 F , 连接 AF , 若 CE= 2, ∠ DAB= 30°, 求 AF 的长 . 图 22-10 考向二　矩形中的折叠问题 图 22-11 【 方法点析 】 矩形的折叠会出现一线三等角模型 , 可利用相似进行计算 , 角平分线遇到平行线会出现等腰三角形 , 对称点连线被对称轴垂直平分 , 利用等腰三角形、垂直平分线的性质可将线段转化 ; 折叠一般会出现直角三角形 , 解题多会用到勾股定理 . | 考向精练 | 1 . [2019· 扬州 ] 将一个矩形纸片折叠成如图 22-12 所示的图形 , 若∠ ABC= 26°, 则∠ ACD= 　　　　 .  图 22-12 [ 答案 ] 128° [ 解析 ] 如图 , 由矩形折叠性质可知∠ ACB= ∠ BCE= ∠ ABC= 26°, 则∠ ACD= 180°-26°-26° = 128° .. 图 22-13 3 . [2019· 杭州 ] 如图 22-14, 把某矩形纸片 ABCD 沿 EF , GH 折叠 ( 点 E , H 在 AD 边上 , 点 F , G 在 BC 边上 ), 使点 B 和点 C 落在 AD 边上同一点 P 处 , A 点的对称点为 A' 点 , D 点的对称点为 D' 点 , 若∠ FPG= 90°,△ A'EP 的面积为 4,△ D'PH 的面积为 1, 则矩形 ABCD 的面积等于 　　　　 .  图 22-14 4 . [2017· 江西 12 题 ] 已知点 A (0,4), B (7,0), C (7,4), 连接 AC , BC 得到矩形 AOBC. 点 D 在边 AC 上 , 将边 OA 沿 OD 折叠 , 点 A 的对应点为 A' , 若点 A' 到矩形较长两对边的距离之比为 1 ∶ 3, 则点 A' 的坐标为 　　　　 .  5 . [2019· 盐城 ] 如图 22-15 ①是一张矩形纸片 , 按以下步骤进行操作 : (I) 将矩形纸片沿 DF 折叠 , 使点 A 落在 CD 边上点 E 处 , 如图 22-15 ② ; (II) 在第一次折叠的基础上 , 过点 C 再次折叠 , 使得点 B 落在边 CD 上点 B' 处 , 如图 22-15 ③ , 两次折痕交于点 O ; (III) 展开纸片 , 分别连接 OB , OE , OC , FD , 如图 22-15 ④ . 【 探究 】 (1) 证明 :△ OBC ≌△ OED ; (2) 若 AB= 8, 设 BC 为 x , OB 2 为 y , 求 y 关于 x 的关系式 . 图 22-15 解 :(1) 证明 : 由折叠可知 AD=AF=DE , ∴ CB=DE. 由两次折叠可知∠ BCO= ∠ DCO= ∠ ODE= 45°, ∴ △ OCD 是等腰直角三角形 , OC=OD , ∴ △ OBC ≌△ OED. 5 . [2019· 盐城 ] 如图 22-15 ①是一张矩形纸片 , 按以下步骤进行操作 : (I) 将矩形纸片沿 DF 折叠 , 使点 A 落在 CD 边上点 E 处 , 如图 22-15 ② ; (II) 在第一次折叠的基础上 , 过点 C 再次折叠 , 使得点 B 落在边 CD 上点 B' 处 , 如图 22-15 ③ , 两次折痕交于点 O ; (III) 展开纸片 , 分别连接 OB , OE , OC , FD , 如图 22-15 ④ . 【 探究 】 (2) 若 AB= 8, 设 BC 为 x , OB 2 为 y , 求 y 关于 x 的关系式 . 图 22-15