呼和浩特专版2020中考数学复习方案第六单元圆提分微课04构造辅助圆课件 26页

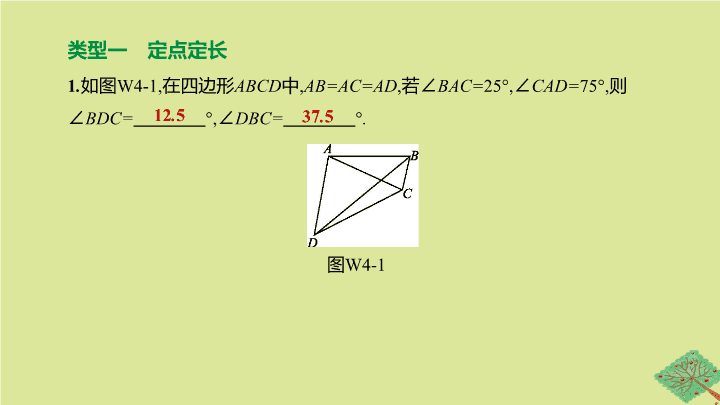
提分微课 ( 四 ) 　　　 构造辅助圆 第六单元　圆 　　 “ 隐圆 ” 一般有如下呈现方式 : ① 定点定长 : 当遇到同一个端点出发的等长线段时 , 通常以这个端点为圆心 , 等线段长为半径构造辅助圆 ; ② 定弦定角 : 当遇到动点对定线段所张的角为定值时 , 通常把张角转化为圆周角构造辅助圆 . 当遇到直角时 , 通常以斜边为直径构造辅助圆 . “ 隐圆 ” 常与线段最值结合考查 . 如图① , 点 A 到圆 O 的最短距离为 AB , 最长距离为 AC. 如图② , 点 A 到圆 O 的最短距离为 AB , 最长距离为 AC. 类型一　定点定长 1 . 如图 W4-1, 在四边形 ABCD 中 , AB=AC=AD , 若∠ BAC= 25°, ∠ CAD= 75°, 则∠ BDC= 　　　　 °, ∠ DBC= 　　　　 ° .  图 W4-1 12 . 5 37 . 5 2 . 如图 W4-2, 在 △ ABC 中 , AC= 6, BC= 8, ∠ ACB= 90°, 将 △ ABC 绕顶点 C 按顺时针方向旋转 , 得到 △ MNC. 点 P , Q 分别是线段 AC , MN 的中点 , 在 △ ABC 绕点 C 按顺时针方向旋转的过程中 , 线段 QP 长度的最小值为 　　　　 , 最大值为 　　　　 .  图 W4-2 2 8 3 . 如图 W4-3, 在 Rt△ ABC 中 , ∠ C= 90°, AC= 6, BC= 8, 点 F 在边 AC 上 , 并且 CF= 2, 点 E 为边 BC 上的动点 , 将 △ CEF 沿直线 EF 翻折 , 点 C 落在点 P 处 , 则点 P 到边 AB 距离的最小值是 　　　　 . 图 W4-3 1.2 4 . 如图 W4-4, 在边长为 4 的菱形 ABCD 中 , ∠ A= 60°, M 是 AD 边的中点 , 点 N 是 AB 边上一动点 , 将 △ AMN 沿 MN 所在的直线翻折得到 △ A'MN , 连接 A'C , 则线段 A'C 长度的最小值是 　　　　 .  图 W4-4 [ 答案 ] 4 [ 解析 ] 如图 : 5 . 在平面直角坐标系 xOy 中 , 已知点 A (2,3), 在 x 轴上找一点 P , 使得 △ AOP 是等腰三角形 , 则这样的点 P 共有 　　　　 个 .  类型二　定弦定角或张角互补 图 W4-5 (1) 直角 6 . 如图 W4-5, 三角板 ACD , BCE 中 ,△ ACD 是等腰直角三角形 , ∠ CAD= ∠ CBE= 90°, 直线 a ∥ CD , 则∠ BCF= 　　　　 .  [ 答案 ] 45° 　 [ 解析 ] 由题意可得 C , B , A , F 四点在同一个圆上 . ∴∠ BFC= ∠ BAC. ∵直线 a ∥ CD , ∴∠ BAC= ∠ ACD. 又∵ △ ACD 是等腰直角三角形 , ∴∠ ACD= 45° . ∴∠ BFC= 45° . ∵∠ CBF= 90°, ∴∠ BCF= 45° . 7 . [2016· 宁波考纲 ] 如图 W4-6, 在等腰直角三角形 ABC 中 , AB=BC= 2, 点 P 为等腰直角三角形 ABC 所在平面内一点 , 且满足 PA ⊥ PB , 则 PC 的取值范围为 　　　　 . 图 W4-6 8 . 如图 W4-7, E , F 是正方形 ABCD 的边 AD 上两个动点 , 满足 AE=DF , 连接 CF 交 BD 于点 G , 连接 BE 交 AG 于点 H , 连接 DH , 若正方形的边长是 2, 则线段 DH 长度的最小值是 　　　　 .  图 W4-7 9 . 如图 W4-8, AC= 3, BC= 5, 且∠ BAC= 90°, D 为 AC 上一动点 , 以 AD 为直径作圆 , 连接 BD 交圆于点 E , 连接 CE , 则 CE 的最小值为 　　　　 .  图 W4-8 10 . [2015· 淮安改编 ] 将一张正方形纸片 ABCD 折叠 , 再展开 , 如图 W4-9 所示 , 其中 CE , CF 为折痕 , ∠ BCE= ∠ ECF= ∠ FCD , 点 B' 为点 B 的对应点 , 点 D' 为点 D 的对应点 , EB' , FD' 相交于点 O. 连接 AB' , 则∠ AB'E 的度数为 　　　　 .  图 W4-9 45° 图 W4-10 (2) 定角 11 . 如图 W4-10,△ ABC 为等边三角形 , AB= 2, 若点 P 为 △ ABC 内一动点 , 且满足∠ PAB= ∠ ACP , 则线段 PB 长度的最小值为 　　　　 .  12 . 如图 W4-11, 等边三角形 ABC 边长为 6, AB 边中点为 F , 动点 D , E 分别从 A , B 两点同时出发 , 以相同的速度沿直线向各自终点 C , A 运动 , 连接 BD , CE , 交于点 P , 则线段 PF 的最小值为 　 　　　 .  图 W4-11 13 . [2018· 徐州 28 节选 ] 如图 W4-12, 将等腰直角三角形 ABC 对折 , 折痕为 CD. 展平后 , 再将点 B 折叠在边 AC 上 ( 不与 A , C 重合 ), 折痕为 EF , 点 B 在 AC 上的对应点为 M , 设 CD 与 EM 交于点 P , 连接 PF. 随着点 M 在边 AC 上取不同的位置 ,△ PFM 的形状是否发生变化 ? 请说明理由 . 图 W4-12 14 . [2016· 宿迁 ] 已知 △ ABC 是等腰直角三角形 , AC=BC= 2, D 是边 AB 上一动点 ( A , B 两点除外 ), 将 △ CAD 绕点 C 按逆时针方向旋转角 α 得到 △ CEF , 其中点 E 是点 A 的对应点 , 点 F 是点 D 的对应点 . (1) 如图 W4-13 ① , 当 α= 90° 时 , G 是边 AB 上一点 , 且 BG=AD , 连接 GF. 求证 : GF ∥ AC. (2) 如图② , 当 90°≤ α ≤180° 时 , AE 与 DF 相交于点 M. ①当点 M 与点 C , D 不重合时 , 连接 CM , 求∠ CMD 的度数 ; ②设 D 为边 AB 的中点 , 当 α 从 90° 变化到 180° 时 , 求点 M 运动的路径长 . 图 W4-13 14 . [2016· 宿迁 ] 已知 △ ABC 是等腰直角三角形 , AC=BC= 2, D 是边 AB 上一动点 ( A , B 两点除外 ), 将 △ CAD 绕点 C 按逆时针方向旋转角 α 得到 △ CEF , 其中点 E 是点 A 的对应点 , 点 F 是点 D 的对应点 . (2) 如图② , 当 90°≤ α ≤180° 时 , AE 与 DF 相交于点 M. ①当点 M 与点 C , D 不重合时 , 连接 CM , 求∠ CMD 的度数 ; 图 W4-13 14 . [2016· 宿迁 ] 已知 △ ABC 是等腰直角三角形 , AC=BC= 2, D 是边 AB 上一动点 ( A , B 两点除外 ), 将 △ CAD 绕点 C 按逆时针方向旋转角 α 得到 △ CEF , 其中点 E 是点 A 的对应点 , 点 F 是点 D 的对应点 . (2) 如图② , 当 90°≤ α ≤180° 时 , AE 与 DF 相交于点 M. ②设 D 为边 AB 的中点 , 当 α 从 90° 变化到 180° 时 , 求点 M 运动的路径长 . 图 W4-13