2020九年级数学下册 第二章 二次函数 7页

课时作业(十八)‎ ‎[第二章　5　第2课时　利用二次函数的图象求一元二次方程的近似根]‎ 一、选择题 ‎1．根据下列表格中二次函数y＝ax2＋bx＋c的自变量x与函数值y的对应值，判断方程ax2＋bx＋c＝0的一个根x的范围是(　　)‎ x ‎6.17‎ ‎6.18‎ ‎6.19‎ ‎6.20‎ y＝ax2＋bx＋c ‎－0.03‎ ‎－0.01‎ ‎0.02‎ ‎0.06‎ A.6＜x＜6.17 B．6.17＜x＜6.18‎ C．6.18＜x＜6.19 D．6.19＜x＜6.20‎ ‎2．如图K－18－1为二次函数y＝ax2＋bx＋c的部分图象，由图象可知 图K－18－1‎ 关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1＝1.6，x2＝(　　)‎ A．－1.6‎ B．3.2‎ C．4.4‎ D．以上都不对 ‎3．借助二次函数y＝2x2－3x－1的图象，可求出下面哪个方程的近似根(　　)‎ A．x2＋5x－1＝0 B．2x2＋3x－1＝0‎ C．2x2－3x＋5＝6 D．x2＋5x＝0‎ ‎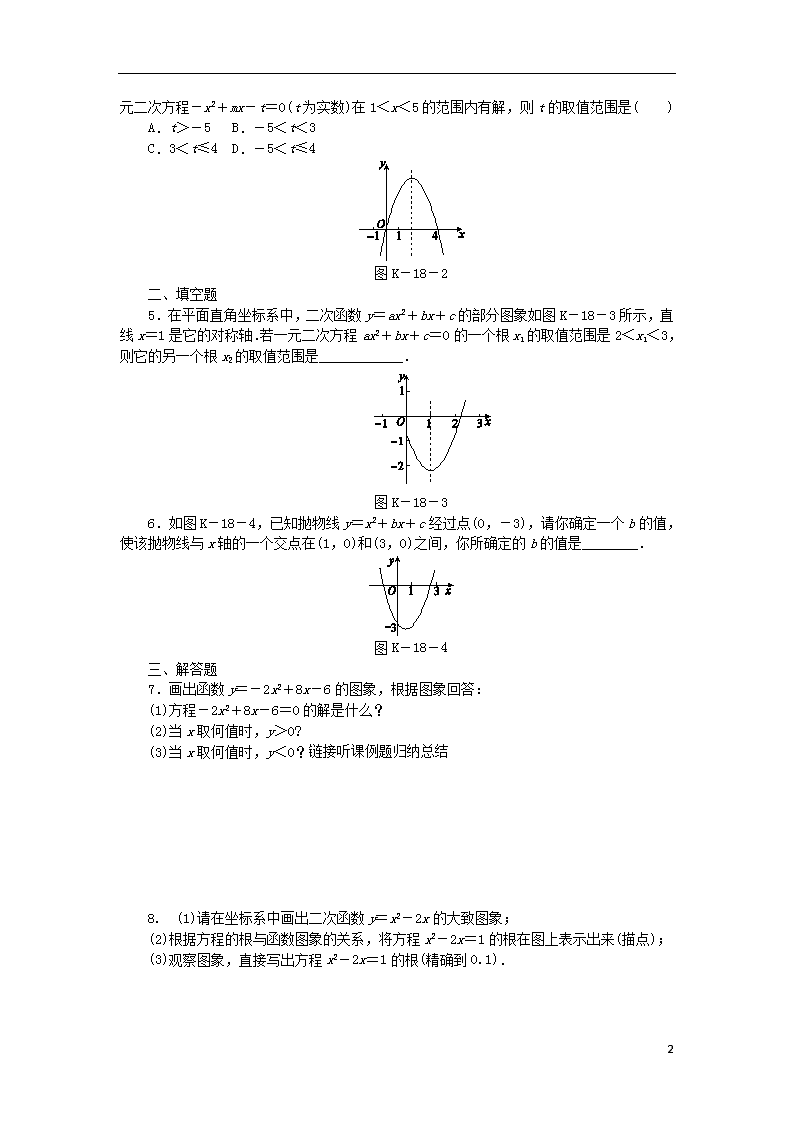4．二次函数y＝－x2＋mx的图象如图K－18－2，其对称轴为直线x＝2，若关于x 7‎ 的一元二次方程－x2＋mx－t＝0(t为实数)在1＜x＜5的范围内有解，则t的取值范围是(　　)‎ A．t＞－5 B．－5＜t＜3‎ C．3＜t≤4 D．－5＜t≤4‎ 图K－18－2‎ 二、填空题 ‎5．在平面直角坐标系中，二次函数y＝ax2＋bx＋c的部分图象如图K－18－3所示，直线x＝1是它的对称轴．若一元二次方程ax2＋bx＋c＝0的一个根x1的取值范围是2＜x1＜3，则它的另一个根x2的取值范围是____________．‎ ‎　　　‎ 图K－18－3‎ ‎6．如图K－18－4，已知抛物线y＝x2＋bx＋c经过点(0，－3)，请你确定一个b的值，使该抛物线与x轴的一个交点在(1，0)和(3，0)之间，你所确定的b的值是________．‎ 图K－18－4‎ 三、解答题 ‎7．画出函数y＝－2x2＋8x－6的图象，根据图象回答：‎ ‎(1)方程－2x2＋8x－6＝0的解是什么？‎ ‎(2)当x取何值时，y＞0?‎ ‎(3)当x取何值时，y＜0？ ‎8. 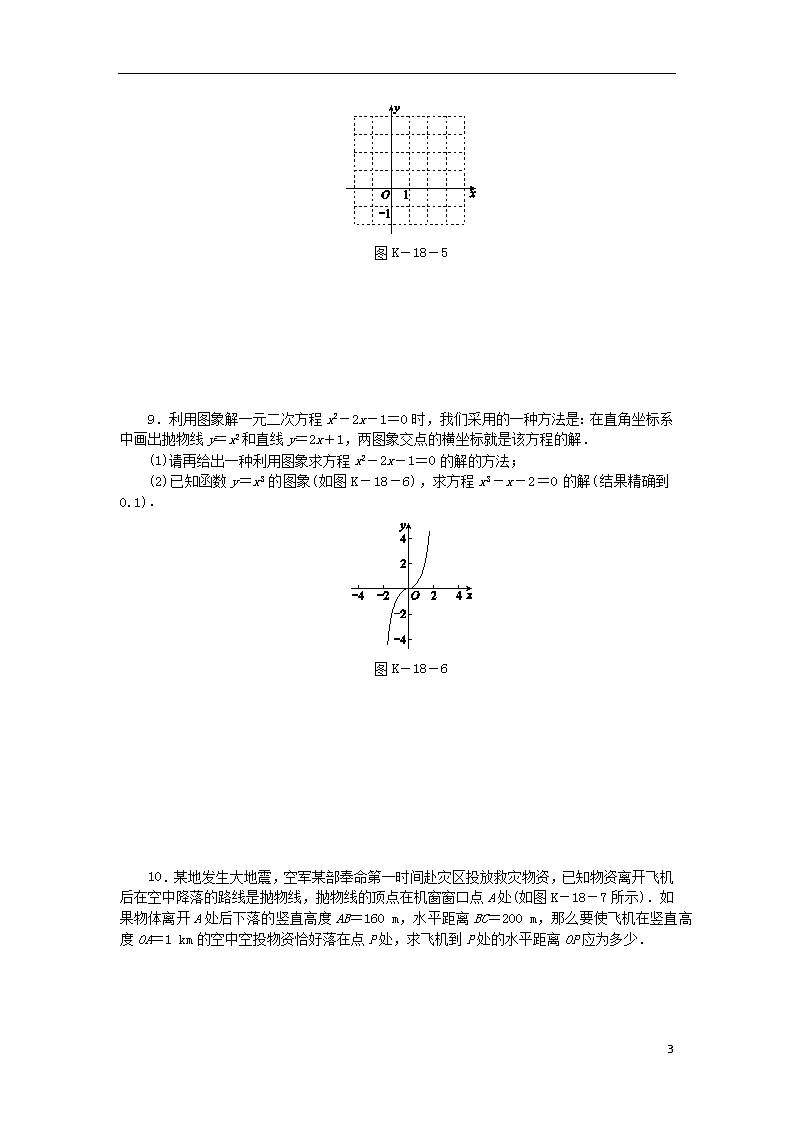(1)请在坐标系中画出二次函数y＝x2－2x的大致图象；‎ ‎(2)根据方程的根与函数图象的关系，将方程x2－2x＝1的根在图上表示出来(描点)；‎ ‎(3)观察图象，直接写出方程x2－2x＝1的根(精确到0.1)．‎ 7‎ 图K－18－5‎ ‎9．利用图象解一元二次方程x2－2x－1＝0时，我们采用的一种方法是：在直角坐标系中画出抛物线y＝x2和直线y＝2x＋1，两图象交点的横坐标就是该方程的解．‎ ‎(1)请再给出一种利用图象求方程x2－2x－1＝0的解的方法；‎ ‎(2)已知函数y＝x3的图象(如图K－18－6)，求方程x3－x－2＝0的解(结果精确到0.1)．‎ 图K－18－6‎ ‎10．某地发生大地震，空军某部奉命第一时间赴灾区投放救灾物资，已知物资离开飞机后在空中降落的路线是抛物线，抛物线的顶点在机窗窗口点A处(如图K－18－7所示)．如果物体离开A处后下落的竖直高度AB＝‎160 m，水平距离BC＝‎200 m，那么要使飞机在竖直高度OA＝‎1 km的空中空投物资恰好落在点P处，求飞机到P处的水平距离OP应为多少．‎ 7‎ 图K－18－7‎ 阅读理解阅读材料，解答问题．‎ 例：用图象法解一元二次不等式：x2－2x－3＞0.‎ 解：设y＝x2－2x－3，则y是x的二次函数．‎ ‎∵a＝1＞0，∴抛物线开口向上．‎ 又∵当y＝0时，x2－2x－3＝0，‎ 解得x1＝－1，x2＝3，‎ ‎∴由此可得二次函数y＝x2－2x－3的大致图象如图K－18－8所示．‎ 观察函数图象可知：当x＜－1或x＞3时，y＞0，‎ ‎∴不等式x2－2x－3＞0的解集是x＜－1或x＞3.‎ ‎(1)观察图象，直接写出一元二次不等式x2－2x－3＜0的解集是__________；‎ ‎(2)仿照上例，用图象法解一元二次不等式：x2－1＞0.‎ 图K－18－8‎ 7‎ 详解详析 ‎【课时作业】‎ ‎[课堂达标]‎ ‎1．[解析] C　由于当x＝6.18时，y＝－0.01<0；当x＝6.19时，y＝0.02>0，说明在6.18＜x＜6.19中有一个x的值使y＝0，即在这个范围内有一个x的值使ax2＋bx＋c＝0.故选C.‎ ‎2．[解析] C　由图象可知其对称轴为直线x＝3，又抛物线是轴对称图形，∴抛物线与x轴的两个交点关于x＝3对称，而关于x的一元二次方程ax2＋bx＋c＝0的两个根分别是x1，x2，那么两根满足2×3＝x1＋x2，而x1＝1.6，∴x2＝4.4.‎ ‎3．[答案] C ‎4．[解析] D　如图，关于x的一元二次方程－x2＋mx－t＝0的解就是抛物线y＝－x2＋mx与直线y＝t的交点的横坐标，当x＝1时，y＝3，当x＝5时，y＝－5，由图象可知若关于x的一元二次方程－x2＋mx－t＝0(t为实数)在1＜x＜5的范围内有解，则直线y＝t在直线y＝－5和直线y＝4之间(包括直线y＝4)，∴－5＜t≤4.故答案为D.‎ ‎5．[答案] －1＜x2＜0　‎ ‎[解析] 由图象可知当x＝2时，y＜0；当x＝3时，y＞0.由于直线x＝1是它的对称轴，则由二次函数图象的对称性可知：当x＝0时，y＜0；当x＝－1时，y＞0.所以另一个根x2的取值范围为－1＜x2＜0.故答案为－1＜x2＜0.‎ ‎6．[答案] (答案不唯一)‎ ‎7．[解析] 利用描点、连线的方法画出函数y＝－2x2＋8x－6的图象，再根据图象判断函数的增减性．‎ 解：函数y＝－2x2＋8x－6的图象如图．‎ 由图象可知：‎ ‎(1)方程－2x2＋8x－6＝0的解是x1＝1，x2＝3.‎ ‎(2)当1＜x＜3时，y＞0.‎ ‎(3)当x＜1或x＞3时，y＜0.‎ ‎8．解：(1)如图．‎ ‎(2)如图，点M，N的横坐标就是方程x2－2x＝1的根．‎ 7‎ ‎(3)方程x2－2x＝1的根为x1≈－0.4，x2≈2.4(答案合理即可)．‎ ‎9．解：(1)答案不唯一，如在直角坐标系中画出抛物线y＝x2－1和直线y＝2x，两图象交点的横坐标就是该方程的解．‎ ‎(2)在图中画出直线y＝x＋2，其与函数y＝x3的图象交于点B，得点B的横坐标x≈1.5，‎ ‎∴方程x3－x－2＝0的解为x≈1.5.‎ ‎10．[解析] 由题意可知点A与点C的坐标，然后可求出抛物线的函数表达式．‎ 解：由题意可知抛物线的顶点坐标为(0，1000)，点C的坐标为(200，840)．‎ 设抛物线的函数表达式为y＝ax2＋1000.‎ 又∵点C(200，840)在抛物线上，‎ ‎∴840＝a×2002＋1000，解得a＝－，‎ ‎∴抛物线的函数表达式为y＝－x2＋1000.‎ 当y＝0时，－x2＋1000＝0，‎ 解得x1＝500，x2＝－500(舍去)．‎ ‎∴飞机到P处的水平距离OP应为500 m.‎ ‎【素养提升】‎ ‎[解析] (1)由图象可得不等式x2－2x－3＜0的解集是－1＜x＜3；‎ ‎(2)仿照(1)的方法，画出函数y＝x2－1的图象，找出图象与x轴的交点坐标，根据图象的开口方向及函数值的符号，确定x的范围．‎ 解：(1)－1＜x＜3‎ ‎(2)设y＝x2－1，则y是x的二次函数．‎ 7‎ ‎∵a＝1＞0，‎ ‎∴抛物线开口向上．‎ 又∵当y＝0时，x2－1＝0，‎ 解得x1＝－1，x2＝1，‎ ‎∴由此可得二次函数y＝x2－1的大致图象如图所示．‎ 观察函数图象可知：当x＜－1或x＞1时，y＞0，‎ ‎∴不等式x2－1＞0的解集是x＜－1或x＞1.‎ 7‎