刹车距离与二次函数教案2 7页

‎2.3　刹车距离与二次函数 教学目标 ‎(一)教学知识点 ‎1．能作出y＝ax2和y＝ax2＋c的图象．并研究它们的性质．‎ ‎2．比较y＝ax2和y＝ax2＋c的图象与y＝x2的异同．理解a与c对二次函数图象的影响．‎ ‎(二)能力训练要求 ‎1．经历探索二次函数y＝ax2和y＝ax2＋c的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验．‎ ‎2．通过比较y＝ax2，y＝ax2＋c与y＝x2的图象和性质的比较，培养学生的比较、鉴别能力．‎ ‎(三)情感与价值观要求 ‎1．由“刹车距离”与二次函数的关系．体会二次函数是某些实际问题的数学模型．‎ ‎2．由有趣的实际问题，使学生能积极参与数学学习活动，对数学有好奇心和求知欲．‎ 教学重点 ‎1．能作出y＝ax2和y＝ax2＋c的图象，并能够比较它们与y＝x2的异同，理解a与c对二次函数图象的影响．‎ ‎2．能说出y＝ax2和y＝ax2＋c图象的开口方向；对称轴和顶点坐标．‎ 教学难点 能作出函数y＝ax2和y＝ax2＋c的图象，并总结其性质，还能和y＝x2作比较．‎ 教学方法 类比学习法．‎ 教具准备 投影片三张 第一张：(记作§2．3A)‎ 第二张：(记作§2．3B)‎ 7‎ 第三张：(记作§2．3C)‎ 教学过程 Ⅰ．创设问题情境，引入新课 ‎[师]在前两节课我们学习了二次函数的定义，会画函数y＝x2与y＝－x2的图象，知道它们的图象是抛物线，并且还研究了抛物线的有关性质．如图象与x轴是否有交点，交点坐标是什么？y随x的增大而如何变化．抛物线是否为轴对称图形等．‎ 那么二次函数是否只有y＝x2与y＝－x2这两种呢？本节课我们继续学习其他形式的二次函数．‎ Ⅱ．新课讲解 一、刹车距离与二次函数的关系．‎ ‎[师]大家知道两辆车在行驶时为什么要保持一定距离吗？‎ ‎[生]怕发生“追尾”事故．‎ ‎[师]汽车刹车时向前滑行的距离与什么因素有关呢？‎ ‎[生]与汽车行驶的速度有关系．‎ ‎[师]究竟与什么有关，关系有多大呢？‎ 投影片：(§2．3A)‎ 影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数．有研究表明，晴天在某段公路上行驶时，速度为v(km／h)的汽车的刹车距离s(m)可以由公式s＝v2确定；‎ 雨天行驶时，这一公式为s＝v2．‎ ‎[师]刹车距离s与速度v之间的关系是二次函数吗？‎ ‎[生]根据二次函数的定义可知，它们都是二次函数．‎ ‎[师]与上节课中学习的二次函数y＝x2和y＝－x2有什么不同吗？‎ ‎[生]y＝x2中的a为1．‎ s＝v2中的a为．‎ 所以它们的不同之处在于a的取值不同．‎ ‎[师]很好．‎ 7‎ 既然s＝v2和s＝v2与y＝x2，y＝－x2它们都是二次函数，且都是只含二次项的二次函数，所以它们有相同之处；又因为它们中的a值的不同．所以它们肯定还有不同之处．比如在y＝x2中自变量x可以取正数或负数，在s＝v2中，因为v是速度，能否取负值呢？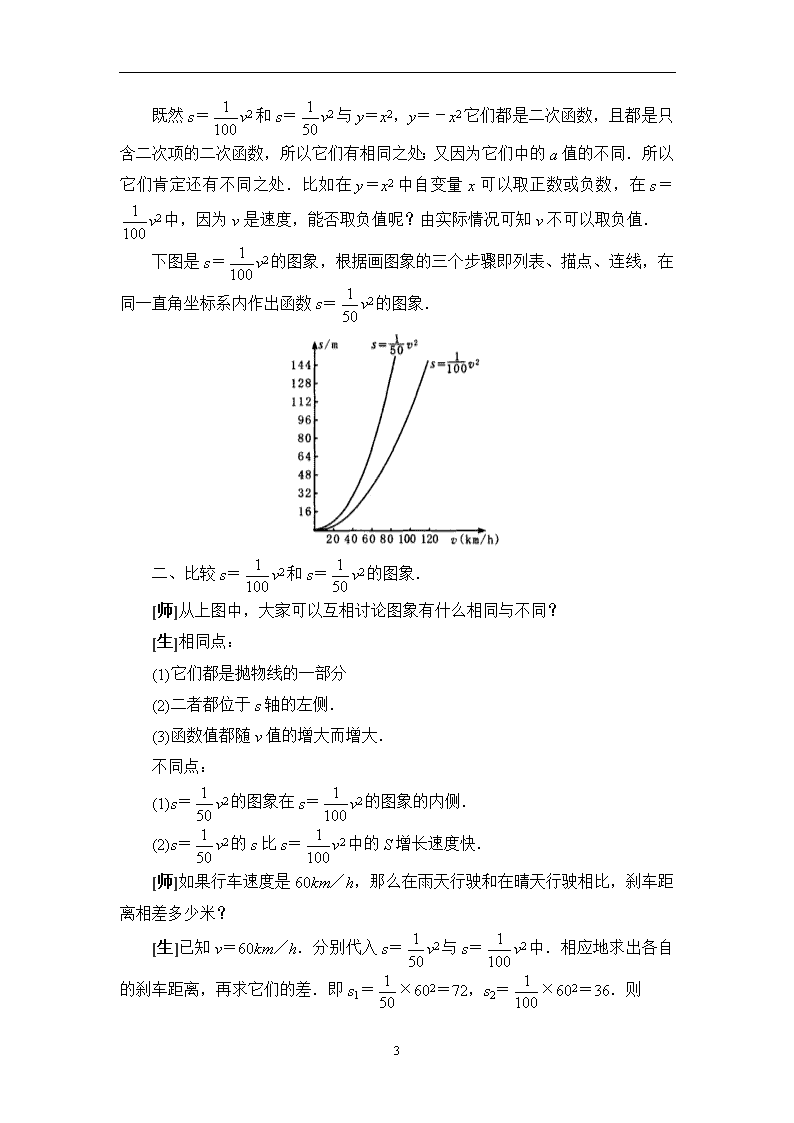由实际情况可知v不可以取负值．‎ 下图是s＝v2的图象，根据画图象的三个步骤即列表、描点、连线，在同一直角坐标系内作出函数s＝v2的图象．‎ 二、比较s＝v2和s＝v2的图象．‎ ‎[师]从上图中，大家可以互相讨论图象有什么相同与不同？‎ ‎[生]相同点：‎ ‎(1)它们都是抛物线的一部分 ‎(2)二者都位于s轴的左侧．‎ ‎(3)函数值都随v值的增大而增大．‎ 不同点：‎ ‎(1)s＝v2的图象在s＝v2的图象的内侧．‎ ‎(2)s＝v2的s比s＝v2中的S增长速度快．‎ ‎[师]如果行车速度是60km／h，那么在雨天行驶和在晴天行驶相比，刹车距离相差多少米？‎ ‎[生]已知v＝60km／h．分别代入s＝v2与s＝v2中．相应地求出各自的刹车距离，再求它们的差．即s1＝×602＝72，s2＝×602＝36．则 7‎ s1－s2＝72－36＝36(m)．‎ 所以在雨天行驶和在晴天行驶相比，雨天的刹车距离较长，相差36m．‎ 三、做一做 投影片：(§2．3B)‎ 作二次函数y＝2x2的图象．‎ ‎(1)完成下表：‎ x ‎2x2‎ ‎(2)在下图中作出y＝2x2的图象．‎ ‎(3)二次函数y＝2x2的图象是什么形状？它与二次函数y＝x2的图象有什么相同和不同？它的开口方向、对称轴和顶点坐标分别是什么？‎ ‎[生](1)略 (2)如图 ‎(3)二次函数y＝2x2的图象是抛物线．‎ 它与二次函数y＝x2的图象的相同点：‎ 开口方向相同，都向上．‎ 对称轴都是y轴．‎ 顶点都是原点，坐标为(0，0)．‎ 在y轴左侧，都是y值随x值的增大而减小；在y轴右侧，都是y值随x值的增大而增大．‎ 都有最低点，即原点．‎ 函数都有最小值．‎ 不同点：y＝2x2的图象在y＝x2的图象的内侧．‎ y＝2x2中函数值的增长速度较快．‎ 四、议一议 投影片：(§2．3C)‎ 7‎ ‎(1)在同一直角坐标系内作出函数y＝2x2与y＝2x2＋1的图象．并比较它们的性质．‎ ‎(2)在同一直角坐标系内作出函数y＝3x2与y＝3x2－1的图象，并比较它们的性质．‎ ‎(3)由上可得出什么？‎ ‎[生](1)图象如下：‎ 比较性质如下：‎ 相同点：‎ a．它们的图象都是抛物线，且形状相同，开口方向相同．‎ b．它们都是轴对称图形，且对称轴都是y轴．‎ c．在y轴左侧，y随x的增大而减小；在y轴右侧，y随x的增大而增大．‎ d．都有最低点，y都有最小值．‎ 不同点：‎ a．它们的顶点不同，y＝2x2的顶点在原点，坐标为(0，0)；y＝2x2＋1的顶点在y轴上，坐标为(0，1)．‎ b．虽然函数y都有最小值，但y＝2x2的最小值为0，y＝2x2＋1的最小值为1．‎ 联系：‎ y＝2x2＋1的图象可以看成函数y＝2x2的图象整体向上平移一个单位．‎ ‎(2)[生]y＝3x2与y＝3x2－1的图象如下：‎ 7‎ 性质比较如下：‎ 相同点：‎ a．它们的图象都是抛物线，且形状相同，开口方向相同．‎ b．它们都是轴对称图形，且对称轴都是y轴．‎ c．都有最低点，函数值都有最小值．‎ d．在y轴左侧，y都是随x的增大而减小，在y轴右侧，y都随x的增大而增大．‎ e．它们的增长速度相同．‎ 不同点：‎ a．它们的顶点不同．y＝3x2的顶点在原点，坐标为(0，0)，y＝3x2－1的顶点在y轴上，坐标为(0，－1)．‎ b．y＝3x2的最小值为0，y＝3x2－1的最小值为－1．‎ 联系：y＝3x2－1的图象可以看成是y＝3x2的图象整体向下平移一个单位．‎ ‎[生](3)可以知道y＝2x2＋1的图象是y＝2x2的图象整体向上移动一个单位得到的．‎ ‎[师]是的．由上可知，y＝ax2与y＝ax2＋c的图象形状相同，开口方向相同，对称轴也相同，只是顶点不同，函数的最大值或最小值不同．y＝ax2＋c的图象可以看成y＝ax2的图象整体上下移动得到的，当c＞0时，向上移动|c|个单位，当c＜0时，向下移动|c|个单位．‎ Ⅲ．课堂练习 画出函数y＝x2与y＝2x2的图象．(在同一直角坐标系内)并比较它们的性质．‎ 分析：画函数图象的步骤有列表、描点、连线．‎ 解：‎ x ‎－4‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ y＝x2‎ ‎8‎ ‎4.5‎ ‎2‎ ‎0.5‎ ‎0‎ ‎0.5‎ ‎2‎ ‎4.5‎ ‎8‎ x ‎－2‎ ‎－1.5‎ ‎－1‎ ‎－0.5‎ ‎0‎ ‎0.5‎ ‎1‎ ‎1.5‎ ‎2‎ 7‎ y＝2x2‎ ‎8‎ ‎4.5‎ ‎2‎ ‎0.5‎ ‎0‎ ‎0.5‎ ‎2‎ ‎4.5‎ ‎8‎ 分别描点画图．‎ 相同点：图象都是抛物线，开口方向相同、顶点相同，都有最低点，函数有最小值．y的值随x的增大而变化情况相同．‎ 不同点：抛物线的开口大小不同，函数值的增长速度不同．‎ Ⅳ．课时小结 本节课巩固了画函数图象的步骤：列表、描点、连线；学习了刹车距离与二次函数的关系；并比较了函数y＝2x2与y＝x2，y＝2x2＋1与y＝2x2，y＝3x2－1与y＝3x2的图象的性质．‎ Ⅴ．课后作业 习题2．3‎ Ⅵ．活动与探究 略 板书设计 ‎§2．3 刹车距离与二次函数 一、1．刹车距离与二次函数的关系(投影片§2．3A)‎ ‎2．比较s＝v2与s＝v2的图象 ‎3．做一做(投影片§2．3B)‎ ‎4．议一议(投影片§2．3C)‎ 二、课堂练习 三、课时小结 四、课后作业 7‎