九年级数学下册第三章圆3圆周角和圆心角的关系第2课时课件北师大版 23页

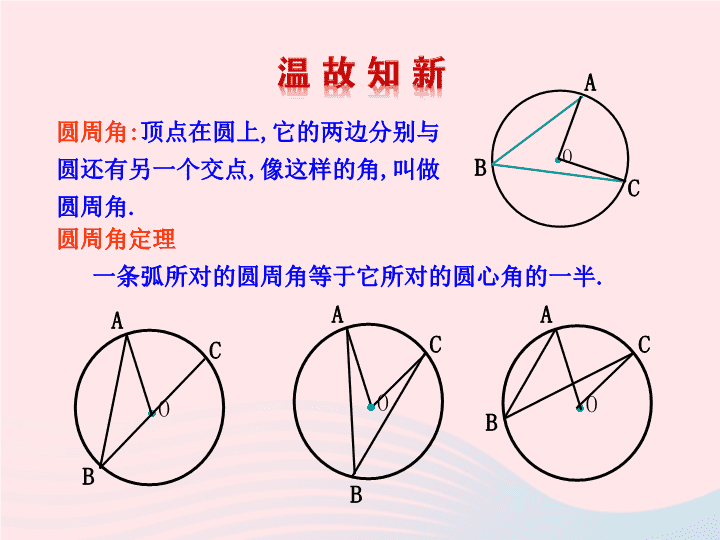
3 圆周角和圆心角的关系 第 2 课时 1. 掌握圆周角定理几个推论的内容 ， 会熟练运用推论解决问题. 2 ．培养学生观察、分析及理解问题的能力 . 3 ．在学生自主探索推论的过程中，经历猜想、推理、验证等环节，获得正确的学习方式 . 圆周角 : 顶点在圆上 , 它的两边分别与圆还有另一个交点 , 像这样的角 , 叫做圆周角 . 圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半 . A B C ● O ● O A B C ● O A B C ● O A B C ● O B B A C D E D E A C 当球员在 B,D,E 处射门时 , 他所处的位置对球门 AC 分别形成三个张角∠ ABC, ∠ADC,∠AEC. 这三个角的大小有什么关系 ? 如图 1, 圆中一段 对着许多个圆周角 , 这些个角的大小有什么关系 ? 为什么 ? 图 2 由此你能得出什么结论 ? ● O B C D E A 图 1 如图 2, 圆中 那么 ∠ C 和∠ G 的大小有什么 关系 ? 为什么 ? 探究 如图 , 圆中∠ C=∠G, 那么 的大小有什么关系 ? 为什么 ? 由此你又能得出什么结论 ? 圆周角定理的推论 1 同圆或等圆中，同弧或等弧所对的圆周角相等 . 用于找相等的角 定理： 1. 如图 (1) ， BC 是⊙ O 的直径， A 是⊙ O 上任一点，你能确定∠ BAC 的度数吗 ? B C O A 图 (1) 2. 如图 (2) ，圆周角∠ BAC =90º ，弦 BC 经过圆心 O 吗？为什么？ 由此你能得出什么结论 ? F E ● B C A 图 (2) O 议一议 用于判断某条弦是否是直径 用于构造直角 圆周角定理的推论 2 直径所对的圆周角是直角； 90° 的圆周角所对的弦是直径 . 推论 1: 同圆或等圆中，同弧或等弧所对的圆周角相等； 推论 2: 直径所对的圆周角是直角； 90° 的圆周角所对的弦是直径 . 推论： ● O D A B C 例 1. 如图 ,AB 是⊙ O 的直径， BD 是 ⊙O 的弦 , 延长 BD 到 C, 使 AC=AB,BD 与 CD 的大小有什么关系 ? 为什么 ? 解析： BD=CD 理由：如图连接 AD. ∵AB 是⊙ O 的直径，∴∠ ADB=90° ， 即 AD⊥BC. 又∵ AC=AB ，∴ BD=CD. 【 例题 】 证明： 如图，连接 AD ， AE. ∠DAB=∠AED ， ∠ EAC= ∠ADE ， ∴ ∠AMN=∠ANM ，∴ AM=AN. ∴△AMN 为等腰三角形 . ● O D A B C N M E 例 2. 如图，⊙ O 中 ,D ， E 分别是 的中点 , DE 分别交 AB 和 AC 于点 M ， N ；求证 :△AMN 是等腰三角形 . ∵ D,E 分别是 的中点 , √ × × × O A B C 1. 判断题： （ 1 ）在同圆或等圆中等弧所对的圆周角相等 . （ ） （ 2 ）相等的圆周角所对的弧也相等 . （ ） （ 3 ） 90° 的角所对的弦是直径 . （ ） （ 4 ）同弦所对的圆周角相等 . （ ） (3) (4) O B A C E 【 跟踪训练 】 2. 填空题 : (1) 如图所示 , ∠BAC= ,∠DAC= . D A B C ∠DBC ∠BDC ● O A C B (2) 如图所示 ,⊙O 的直径 AB=10cm,C 为⊙ O 上一点 ,∠BAC=30°, 则 BC= cm. 5 3. 如图，以⊙ O 的半径 OA 为直径作⊙ O 1 , ⊙O 的弦 AD 交⊙ O 1 于 C, 则 (1)OC 与 AD 的位置关系是 __________________; (2)OC 与 BD 的位置关系是 ___________; (3) 若 OC=2cm, 则 BD=______cm. OC 垂直平分 AD 平行 4 C D O 1 A B O 4. 如图 ,△ABC 的顶点均在⊙ O 上 , AB=4, ∠C=30°, 求⊙ O 的直径 . ● O A C B E 解： 连接 AO 并延长交⊙ O 于点 E ，连接 BE ，∠ E=30°, ∠ABE=90°, 由 AB=4 得直径 AE=8. 5. 如图， AE 是⊙ O 的直径 , △ABC 的顶点都在⊙ O 上 ,AD 是△ ABC 的高 . 求证： AB·AC=AE·AD. A O B C D E 证明：因为 ∠ADB= ∠ACE=90° ， ∠AEC=∠ABD, 故△ ACE∽ △ ADB, 所以 即 AB·AC=AE·AD. 1. （衡阳 · 中考）如图，已知⊙ O 的两条弦 AC ， BD 相交于点 E ，∠ A=70 o ，∠ C=50 o ， 那么 sin∠AEB 的值为（ ） 答案： D A. B. C. D. 2. （荆门 · 中考）如图， MN 是半径为 1 的⊙ O 的直径，点 A 在⊙ O 上，∠ AMN=30° ， B 为弧 AN 的中点，点 P 是直径 MN 上一个动点，则 PA+PB 的最小值为（ ） 答案： B C ． 1 D ． 2 A ． 2 B ． 3 ．（荆州 · 中考）△ ABC 中，∠ A=30° ，∠ C=90° ，作△ ABC 的外接圆．如图，若弧 AB 的长为 12cm ，那么弧 AC 的长是（ ） A ． 10cm B ． 9cm C ． 8cm D ． 6cm 答案： C 【 规律方法 】 圆周角定理建立了圆心角与圆周角的关系， 而同圆或等圆中圆心角、弧、弦之间又存在等量关系，因此，圆中的角（圆周角和圆心角）、弦、弧等的相等关系可以互相转化 . 但转化过程中要注意以圆心角、弧为桥梁 . 如由弦相等只能得弧或圆心角相等，不能直接得圆周角相等 . 1 ．要理解好圆周角定理的推论 . 2 ．构造直径所对的圆周角是圆中的常用方法 . 引辅助线的方法： （ 1 ）构造直径上的圆周角 . （ 2 ）构造同弧所对的圆周角 . 3 ．要多观察图形，善于识别圆周角与圆心角，构造同弧所对的圆周角也是常用方法之一 . 忍耐之草是苦的，但最终会结出甘甜而柔软的果实。 —— 辛姆洛克