二年级上册数学教案-6 整理与提高（数学广场-点图与数）1 ▏沪教版 3页

点图与数（第一课时）‎ 教学内容：上海市九年制义务教育课本数学二年级上册第81页。‎ 教学目标：1、直观认识奇数和偶数。‎ 2、 通过对点图的拼搭，探索奇数和偶数之间加法的简单规律。‎ 3、 经历探究活动和猜想过程，提高按规律合理猜想、推理的能力；在过程中感悟数形结合的思想。‎ 教学重点：通过点图认识奇数、偶数。‎ 教学难点：通过点图探究有关奇数、偶数的一些规律。‎ 教学准备：希沃课件、贴纸板书、1-10的点图学具。‎ 教学过程：‎ 一、 情境引入 1、 师： 瞧，小兔子在花园里画着什么呢？可以用哪个数表示？（依次出示点图1-4）‎ 2、 揭题：这节课我们就一起来学习“点图与数”。（板书：点图与数）‎ ‎3、师：小兔子啊把他手里所有的点图都展示给大家看（出示点图5-10），我们一一来辨认下它们都表示几？‎ 生：表示5、6、7、8、9、10。‎ ‎4、问：你们怎么知道这些点图表示几的？‎ 二、探究新知 ‎（一）认识奇、偶数 ‎1、师：同桌2人一组，互相说一说你准备分几类？怎么分？‎ 交流反馈 ‎2、师：观察1、3、5、7、9这些点图有什么共同特点？（交流）‎ 告知：我们把这样的点图所表示的数叫做“奇数。”（板书：奇数）‎ 问：现在我们屏幕中呈现出表示奇数的点图有哪些？（板书：1、3、5、7、9）‎ 3、 师：那么还有一类，谁来说说另外一类是哪些？仔细观察，这些点图又有什么特点呢？（交流）‎ 师：像这样的点图表示的数称为“偶数”。（板书：偶数）‎ 问：现在我们认识的偶数有哪些？（板书：2、4、6、8、10）‎ （二） 判断奇偶数 1、 师：判断下列点图表示的数是奇数还是偶数？‎ ‎ 依次出示： ‎ ‎2、师：怎么来判断一个点图是表示奇数还是偶数的呢？‎ ‎3、小结：你是观察图形的特点，一边是折的（不是直的），就是奇数；两边都是直的就是偶数。‎ ‎4、师：用两个点图组成的一个新的点图，你能来判断它是奇数还是偶数吗？（依次出示： ）为什么？‎ ‎（三）动手操作 ‎1、师：小兔想邀请大家来参加点图派对啦！先听游戏规则：从1到10的点图中任意选择两个拼一拼。想一想，你准备选哪两个拼？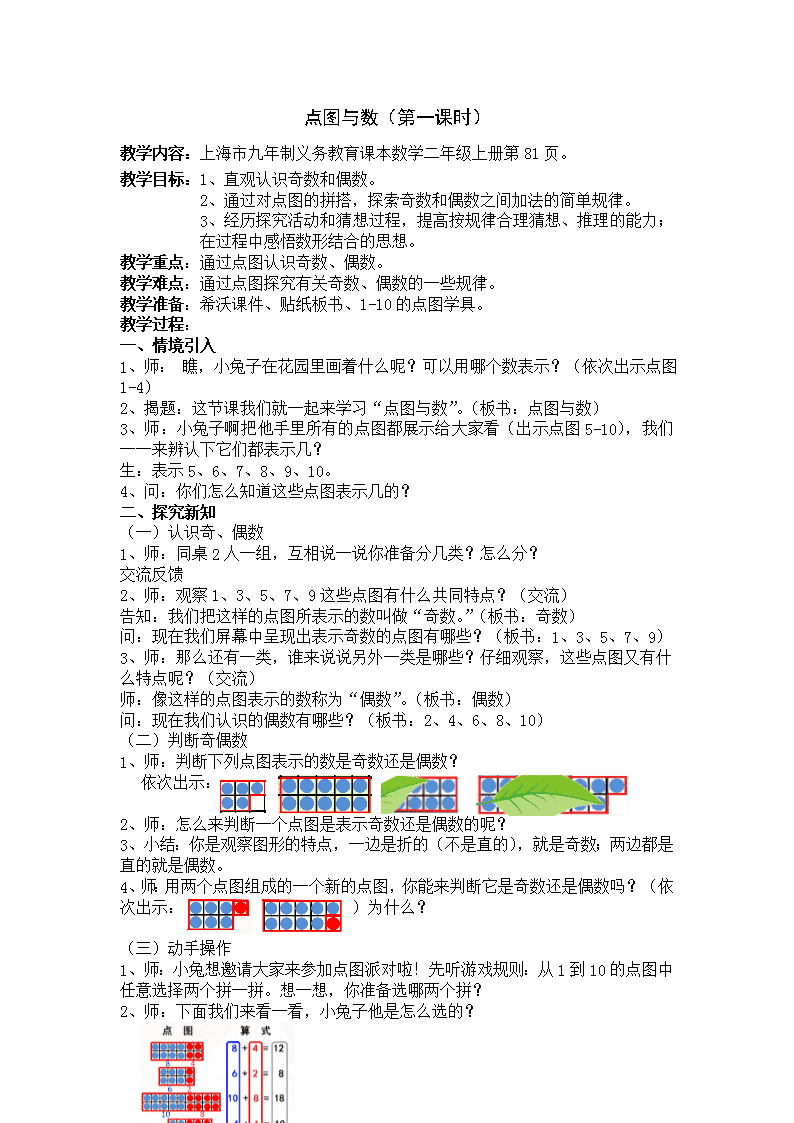‎ 2、 师：下面我们来看一看，小兔子他是怎么选的？‎ 师：观察小兔子依次拿出的蓝色点图表示什么样的数？他第二次拿出的红色点图是什么数呢？它们拼出的新点图又是什么数呢？你能来说说你发现了什么规律吗？‎ 生：偶数+偶数=偶数。‎ 2、 师：看小兔子在那拼一拼，你们想不想也来拼一拼？在拼之前先请我们小朋友来猜一猜，如果是两个奇数的话，它的结果是？第三种情况呢？一个偶数一个奇数的结果会是什么呢？‎ 师：这些都是我们的猜想，还需要我们小朋友去探究验证。接下来请小朋友两人一组，请根据后两种情况，在1到10的点图中选择两张拼一拼，将结果用算式填写在练习单上，拿出信封和学习单。‎ 3、 汇报交流并板书（算式和规律）‎ 奇数+奇数=偶数 奇数+偶数=奇数 ‎3+5=8 5+2=7‎ ‎7+9=16 9+4=13‎ ‎7+5=12 3+8=11‎ 问：刚才上台展示的小朋友拿的都是两张表示什么样的点图？他们拼成的新点图都表示什么数？那你能得到什么样的结论？‎ 4、 师：小兔子说在点图花园里带你们玩了这么久，你们发现了哪些秘密？‎ 生：奇数+奇数=偶数；‎ 奇数+偶数=奇数；‎ 偶数+偶数=偶数。‎ 三、练习巩固 ‎1、数射线上跳远两格一跳，跳到的数都是什么数？奇数除了1.3.5.7.9还有11、13、15……相邻的两个奇数间有什么秘密呢？‎ 第二次小兔是怎么跳的，跳到了哪些数？这些都是什么数?也就是偶数除了2.4.6.810.还有12.14.16.18……相邻两个偶数间有什么关系？‎ 你是如何判断奇数、偶数的？‎ 1、 分类小游戏（连连看）——分奇、偶数 2、 分组竞赛 四、 全课总结 学到了什么？‎ 五、拓展（回家作业）‎ 奇数连加的结果是什么？‎ 偶数连加的结果是什么？‎ 一个奇数一个偶数依次连加的结果是什么？‎ 六、课堂表现评价 七、板书设计 点图与数 奇数：1,3,5,7,9,11,13,15……相邻两个奇数间相差2‎ 偶数: 2,4,6,8,10，12，14,16……相邻两个偶数间相差2‎ 猜想 偶数+偶数=偶数 奇数+奇数=奇数 奇数+偶数=奇数 验证 运用