五年级数学下册课件-总复习PPT课件 人教版 (共159张PPT) 159页

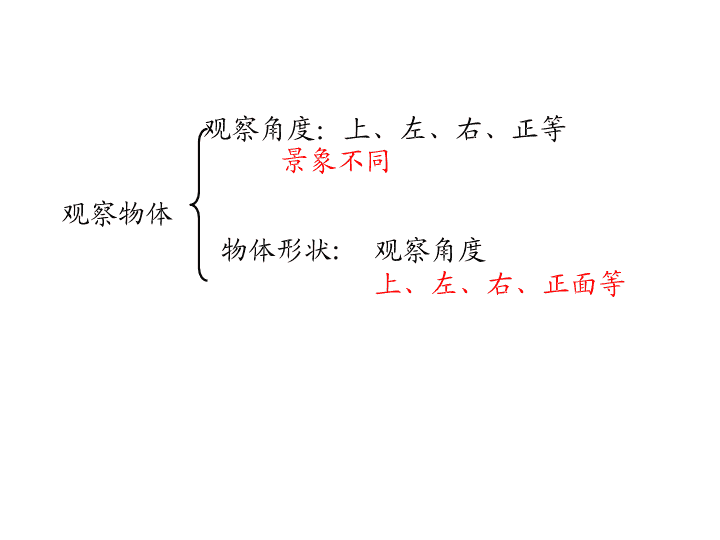
第一单元 观察物体（三） 观察角度：上、左、右、正等 景象不同 物体形状 : 观察角度 上、左、右、正面等 观察物体 一个长方体有（ ）个面，一次最多可以看见（ ）个面。 6 3 2 颗 的是（ ）面； 1 颗 的是（ ）面； 3 颗 的是（ ）面； 正 右 上 连一连 正面 左面 上面 看一看，画一画 从正面看： ____ 从 左面看 ： ____ 从上面看： ____ 从右面看 ： ____ 下面这些图分别是从哪个方向上看到的？ 左面 上面 正面 右面 √ ○ △ √ ○ △ √ ○ △ 4. 从上面观察 所看到的图形是 ( ) A 、 B 、 C 、 5. 从右面观察 所看到的图形是（ ）。 A 、 B 、 C 、 A B 第二单元 因数与倍数 小狗吃骨头 _______ 既是 18 的因数，又是 21 的因数 9 18 4 2 7 6 3 1 21 18 的因数 21 的因数 把 36 个球装在盒子里，每个盒子装得同样多，需要几个盒子？有几种装法？如果有 37 个球呢？ 一个数 只有 1 和它本身 两个 因数，这个数叫作 质数 （也叫作素数）。 一个数，如果 除了 1 和它本身以外， 还有 别的因数，这个数叫作 合数 。 1 既不是 质数， 也不是 合数。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 试着找出100内的所有质数！ 方法： 1, 划去 1 ； 2, 划去除 2 外所有 2 的 倍数； 3, 划掉除 3,5,7 外所有 3, 5,7 的倍数 , 剩下的就 是质数。 除尽 整除 2 、 5 、 3 倍数的特征 自然数 1 质数 合数 质因数 分解质因数 倍数 公倍数 最小公倍数 因数 最大公因数 公因数 因数与倍数 偶数 奇数 易混概念对比 1. 如果甲数是乙数的 5 倍，那么，甲数一定 是乙数的倍数。（ ） 倍的概念比倍数要广，倍可以适用于小数、 分数和整数，而倍数只适用于整数。 例如： 16 是 8 的 2 倍，也可以说 16 是 8 的倍数。 1.6 是 0.8 的 2 倍，但是不能说 1.6 是 0.8 的倍数。 2. 对比几个字面类似的概念：质数、质因数、互质数、分解质因数，使学生清楚它们的含义，并能举例说明。 质数 一个数，如果只有 1 和它本身两个因数，这样的数叫做质数（或素数）。 质因数 每个合数都可以写成几个质数相乘的形式，这几个质数叫做这个合数的质因数。 分解质因数 把一个合数用质因数相乘的形式表示出来，叫做分解质因数。 互质数 公因数只有 1 的两个数，叫做互质数。 易混概念对比 易混概念对比 质数 是一个具体的数，它是相对于一个数的因数的个数而言的 。 质因数 也是一个具体的数，必须是一个质数它是一个合数的因数。 分解质因数 是把一个一个合数分解成几个质数相乘形式的过程。 互质数特殊的判断方法 ① 1 和任意自然数互质。 ②2 和任意奇数都是互质数。 ③ 相邻两个自然数都是互质数。 ④ 相邻的两个奇数都是互质数。 ⑤ 不相同的两个质数是互质数。 ⑥ 当一个数是合数，而另一个数是质数时，若合数不是质数的倍数，一般情况下这两个数也是互质数。 对比中沟通概念间的联系 1. 如：把 1——20 的数字填入下表中： 质 数 合 数 非质非合 奇数 3 、 5 、 7 、 11 、 13 、 17 、 19 9 、 15 1 偶数 2 4 、 6 、 8 、 10 、 12 、 14 、 16 、 18 、 20 2. 出示判断题： （ 1 ）自然数中，除了奇数就是偶数。（ ） （ 2 ）所有的奇数都是质数。 （ ） （ 3 ）所有的合数都是偶数。 （ ） （ 4 ）自然数中，除了质数就是合数。（ ） （ 5 ）质数与质数的积还是质数。 （ ） （ 6 ）一个数越大，它的因数的个数就越多。 （ ） 注意：奇数里既有质数也有合数还有 1 。 质数里除了 2 以外都是奇数。 偶数里除了 2 以外全是合数。 3.奇数和偶数的运算性质 奇数 ± 奇数 = 偶数 偶数 ± 偶数 = 偶数 奇数 ± 偶数 = 奇数 奇数 × 奇数 = 奇数 偶数 × 偶数 = 偶数 奇数 × 偶数 = 偶数 4. 同时是 2 和 5 的倍数的特征 个位上是 0 的数都是 2 和 5 的倍数。 同时是 2 和 3 的倍数的特征 个位上是 0 、 2 、 4 、 6 、 8 ，并且各数位上的数字之和是 3 的倍数，这个数就是 2 和 3 的倍数。 同时是 3 和 5 的倍数的特征 个位上是 0 或 5 ，且各数位上的数字之和是 3 的倍数，这个数就是 3 和 5 的倍数。 同时是 2 、 3 、 5 的倍数的特征 个位上是 0 ，且各数位上的数字之和是 3 的倍数，这个数就同时是 2 、 3 、 5 的倍数。 5. 【 2 、 5 、 3 的倍数的特征 】 按要求填一填。 30 10 42 65 3 18 15 45 5 46 27 72 55 2 120 102 2 的倍数 2 和 3 的公倍数 5 的倍数 3 的倍数 2 和 5 的公倍数 3 和 5 的公倍数 2 、 3 、 5 的公倍数 同时是 2 、 3 倍数的最小数是（）。 同时是 2 、 5 倍数的最大两位数（）。 同时是 3 、 5 倍数的最大两位奇数（）。 同时是 2 、 3 和 5 倍数的最小三位数（）。 求两个数最大公因数的方法： 列举法： 先分别找出两个数的因数，从中找出公因数，再找出最大的一个。 先找出两个数中较小数的因数，从中圈出另一个数的因数，再看哪一个最大？ 分解质因数法： 现将这两个数分别分解质因数，再从分解的质因数中找出公有的质因数，公有的质因数连乘所得的积就是这两个数的最大公因数。 用集合图法。 最大公因数 最小公倍数 所以，（ 18 ， 30 ） =2×3=6 （公有质因数的积） [18 ， 30]= 2×3×3×5=90 （公有质因数与独有质因数的积） 为了便于区分，可以简单归纳为：最大公因数乘半边，最小公倍数乘半圈。 18 30 2 9 15 3 3 5 公有的质因数 独有的质因数 特殊情况 熟练掌握两种特殊情况。 两数关系 最大公因数 最小公倍数 互质关系 1 两数积 倍数关系 较小数 较大数 同时熟记 7 、 11 、 13 、 17 、 19 等数的倍数 及 11—20 所有数的平方数以提高计算速度。 如求 12 和 30 的最小公倍数就可以采用大数扩倍法，把 30 扩大 2 倍为 60 ， 60 是 12 的 5 倍，所以 60 是他们的最小公倍数。 重视口算技巧 18 30 6 3 5 求两个数的最大公因数与最小公倍数时，用合数作除数有助于提高计算速度。 解决问题 小船最初在南岸，从南岸驶向北岸，再从北岸返回南岸，不断往返。 （ 1 ）小船摆渡 11 次后，船在南岸还是北岸？为什么？ （ 2 ）有人说摆渡 100 次后，小船在北岸，他的说法对吗？为什么？ 分析： 在两点间行走，走 奇数次后 到与起点 相对处 ，走 偶数次后 回到 起点处 。 北京站是 104 路和 103 路电车的起发站。 104 路每 3 分发一次车， 103 路每 8 分发一次车，这两路电车同时发车以后，至少再过多少分又同时发车？ 分析： 104 路电车每 3 分发一次车，每次发车时间一定是 3 的倍数，即第二次发车与第一次发车间隔 3 分，第三次发车与第一次发车间隔 6 分，而 103 路电车每 8 分发一次车，每次发车的时间一定是 8 的倍数，即第二次发车与第一次发车间隔 8 分，第三次发车与第一次发车间隔 16 分，这样就找到了每次两路电车同时发车的时间，就是求 3 和 8 的最小公倍数。 小红家的客厅长 48 分米，宽 32 分米。现在给客厅的地面铺正方形地砖，有三种砖，你帮小红家想一想，选择哪种地砖能铺得即整齐又不会有余料？ 边长 3 分米 边长 6 分米 边长 8 分米 分析： 求出 48 和 32 的公因数，这个公因数是地砖的边长。 复习长方体和正方体 第一课时 长方形 正方形 三角形 按边分 按角分 等边三角形 等腰三角形 一般三角形 锐角三角形 直角角三角形 钝角三角形 平行四边形 梯形 等腰梯形 直角梯形 一般梯形 组合图形 平面图形 一、建构知识网络 立体图形 正方体 长方体 二、 注重知识的承接，回顾所学平面图形的特征、周长和面积公式。 名称 特征 周长（ c ） 面积（ s ） 长方形 两组对边分别平行且相等 （长＋宽） ×2 C=2(a ＋ b) 长 × 宽 S=ab 正方形 四边相等 边长 ×4 C=4a 边长 × 边长 S=a ² 平行四边形 两组对边平行且相等 底 × 高 S=ah 梯形 只有一组对边平行 （上底＋下底） × 高 ÷2 三角形 三条边，三个内角的和等于 18 0° （底 × 高） ÷2 ah S= 1 2 ( a+b)h S= 1 2 三、 明确长方体、正方体的异同。 从点、棱、面三方面比较长方体和正方体之间的相同点和不同点 长方体 正方体 相同点 6 个面、 12 条棱、 8 个顶点 不同点 6 个面都是长方形（有时相对的两个面是正方形），相对面完全相同。 6 个面都是正方形， 6 个面完全相同 相对棱的长度相等 12 条棱长度都相等 正方体是特殊的长方体。 用集合图表示： 长方体 正方体 四、 复习长方体、正方体表面积的含义 15 10 8 后 前 上 下 左 右 ● 15 10 8 单位：厘米 长方体六个面的面积，就是长方体的表面积。 1. 长方体表面积的含义 2 ．正方体表面积的含义 （ 1 ）正方体棱长与每个面边长的关系 后 上 前 下 左 右 正方体展开图的每个面都是正方形，边长就是正方体的棱长，每个面的面积都等于棱长乘棱长。 （ 2 ）正方体的 11 种展开图。 图（ 1 ） 图（ 2 ） 图（ 3 ） 图（ 4 ） 图（ 5 ） 图（ 6 ） 第一类：中间四连方，两侧各有一个，共 6 种 第二类：中间三连方，一侧有一个、一侧有二个，共 3 种 图（ 7 ） 图（ 8 ） 图（ 9 ） 第三类：中间两连方，两侧各有 2 个，只有 1 种 图（ 10 ） 第四类：两排各有 3 个，只有 1 种 图（ 11 ） 长方体 正方体 12 7 5 5 5 5 一间教室长 10 米 , 宽 6 米 , 高 4 米 , 现要粉刷屋顶和四壁 , 除去门窗 面积 20 平方米 , 如果每平方米需 工料费 1.5 元 , 粉刷这间教室共需 工料费多少元 ? 五、复习长方体、正方体体积公式的推导 长方体的体积 = 长 × 宽 × 高 底面积 正方体的体积 = 棱长 × 棱长 × 棱长 底面积 可看作是高 长方体（或正方体）的 体积 = 底面积 × 高 六、体积与容积区别与联系 异同点 体积 容积 区别 意义不同 物体所占空间的大小，叫做物体的体积。 一个容器所能容纳物体的体积，叫做这个容器的容积。 测量方法不同 从物体外部测量长、宽、高。 从容器里面测量长、宽、高。 单位名称不同 m³ 、 dm³ 、 cm³ 。 容积单位： L 和 ml; 计量固体时用体积单位。 联系 容积的大小是通过所能容纳物体的体积表示出来的。 计算方法相同 7 厘米 5 厘米 5 厘米 这个长方体的长是（ 7 ）厘米，宽是（ 5 ）厘米，高是（ 5 ）厘米，这个长方体有（ 2 ）个面是正方形，有（ 4 ）个面是长方形。 如图 1 ． 2. 要焊接一个长 10cm ，宽 8cm ，高 6cm 的长方体框架，要准备 10cm ，宽 8cm ，高 6cm 的铁丝各（ 4 ）根。 3 ．一个正方体纸盒的棱长是 7cm ，这个纸盒的棱长总和是（ 84 ） cm 。 4 ．有一根 150cm 长的铁丝，用这根铁丝焊成了一个正方体的框架，还剩铁丝 6cm 。这个正方体框架的棱长是（ ）厘米。 七、基础知识的练习 150cm 12 8. 有一个长方体，底面是一个正方形，高 18cm ，侧面展开正好是一个正方形。这个长方体的体积是（ 364.5 ） cm³ 。 18÷4=4.5 （ cm ） 4.5×4.5×18 =20.25×18 =364.5 （ cm³ ） 18cm 18cm 18cm 10. 把棱长是 1 厘米的小正方体拼摆在一起。如果从右面看，所看到的图形面积是 ( 7 ) 平方厘米，体积是（ 11 ）立方厘米。 11. 一个棱长为 2cm 的正方体，在它的一个角上挖掉一个棱长为 1cm 的小正方体，它的表面积是 （     24 ） cm² 。 第二课时：解决相关的实际问题 12cm 15cm 8cm 1. 一条彩带捆扎一种礼盒（如图），如果接头处的彩带长 30cm ，求这条彩带的长度。 8×4 ＋ 12×2 ＋ 15×2 ＋ 30=116 （ cm ） 答：这条彩带长 116 厘米。 2. 与右面正方体一致的展开图是（ ）。 B 1 2 3 1 2 3 2 3 1 1 2 3 C B A 甲 乙 取出石块后 2.1dm 1.8dm 3. 图中有两个完全一样的长方体水箱，水箱的底面积是 2 平方分米，请结合图中所给信息求出甲箱中石块的体积是多少？ 2×(2.1-1.8)=0.6 （ dm ³ ） 答：石块的体积是 0.6dm ³ 。 前 右 6 3 7 4 ．小明从一个长方体纸盒上撕下两个相邻的面（展开后如图，单位：厘米），这个纸盒的底面积是（ ）平方厘米，体积是（ ）立方厘米。 底面积： 6×3=18 （平方厘米） 18 126 体积： 6×3×7=126 （立方厘米） 5 厘米 5 厘米 5 厘米 5. 把 积木装入纸箱内，纸箱从里面量，长 25 厘米，宽和高都是 20 厘米。纸箱最多可容纳积木多少块？ （ 25÷5 ） × （ 20÷5 ） × （ 20÷5 ） =5×4×4 =80 （块） 答：纸箱最多可容纳积木 80 块。 6. 把 积木装入纸箱内，纸箱从里面量，长 25 厘米，宽和高都是 20 厘米。纸箱最多可容纳积木多少块？ 5 厘米 3 厘米 3 厘米 （ 25÷3 ） × （ 20÷3 ） × （ 20÷5 ） ≈ 8×6×4 =192 （块） 答：纸箱最多可容纳积木 192 块。 7. 一块长方形铁皮，长 40cm, 宽 30cm, 像下图这样从 4 个角各剪掉一个边长为 5 厘米的正方形，然后做成盒子，这个盒子的容积是多少升？ 40cm 30cm （ 40 － 5 × 2 ） × （ 30 － 5 × 2 ） × 5=3000 （ cm³ ） 3000cm³=3L 答： 这个盒子的容积是 3 升。 12ml=12cm3 24ml=24cm3 一个小球的体积： (24-12) ÷(4-1)=4(cm3) 一个大球的体积： 12-4=8(cm3) 左图长、宽、高分别是 4cm 、 3cm 、 3cm 。 它的体积是： 4×3×3=36 （ cm2 ） 右图长、宽、高分别是 4cm 、 3cm 、 4cm 。 它的体积是： 4×3×4=48 （ cm2 ） 10. 用 3 个长 5cm, 宽 4cm, 高 3cm 的长方体木块，拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米？ 5cm 4cm 3cm [5×4 ＋ 5×(3×3) ＋ 4×(3×3)]×2=(20 ＋ 45 ＋ 36)×2=202 （ cm² ） 答：这个长方体的表面积是 202 平方厘米。 3cm 2cm 6cm 6cm 11. 有一个形状如图的零件，由一个长方体和一个 正方体组合而成。长方体的长和宽都是 6cm ，高是 3cm ，正方体的棱长是 2cm 。求这个零件的表面积。 2 × 2 × 4 ＋ 6 × 3 × 4 ＋ 6 × 6 × 2 =16 ＋ 72 ＋ 72 =160 （ cm ² ） 答：这个零件的表面积是 160 平方厘米。 12 ．由 27 个棱长为 1cm 的小正方体组成一个棱长为 3cm 的大正方体，若自上而下去掉中间的 3 个小正方体（如图所示），则剩下的几何体的表面积是多少平方厘米？ 3×3×6 － 1×1×2 ＋ 3×1×4 =54 － 2 ＋ 12 =64 （ cm² ） 答：剩下的几何体的表面积是 64 平方厘米。 13 ．从一个大长方体上切下一个体积是 128 立方厘米的小长方体（如图）。原来大长方体的体积是多少立方厘米？ 22cm 8cm 切下部分 128÷8×22 =16×22 =352 （立方厘米） 答：原来大长方体的体积是 352 立方厘米。 14. 一个密封的长方体容器里面装有一些水，水深 9 厘米，如果把这个容器的右面做底，这时容器内的水深多少厘米？ 36 10 12 36 10 12 36×10×9=3240 （ cm3 ） 3240÷(12×10)=27 （ cm ） 答：容器内的水深 27 厘米。 第四单元 分数的意义和性质 分数 分数的意义 分数单位 分子分母的意义 分数与除法的关系 分数大小的比较 分数的分类 真分数 假分数 整数 带分数 分数的基本性质 约分 通分 求一个数是另一个数的几分之几 分数和小数的互化 3 4 6 8 12 16 = = 2 3 4 6 8 12 = = 火眼金睛 观察等式，你有什么发现？ 分数的分子和分母都乘或除以相同的数（ 0 除外），分数的大小不变。 12 16 10 12 6 30 把最简分数的气球放飞 把其余气球上的分数约分 2 3 7 18 25 45 在相同时间内，贝贝跑了全程的　，欢欢跑了全程的　，谁跑的快呢？ ５６ ６７ 1 6 和 5 9 3 5 和 4 7 5 6 和 3 4 把上面各组分数通分 . 5 12 和 4 9 计算下面各题 . 3 10 + 7 10 5 6 － 1 6 4 7 － 1 3 7 8 － 3 4 2 3 + 7 9 1 6 + 1 5 － 1 2 同分母分数相加、减， 分母不变， 只把分子相加、减． 异分母分数相加、减， 先通分， 然后按照同分母分数加、 减法的计算法则进行计算． 六一儿童节 , 五一班参加唱歌表演的 占全班学生人数的 , 跳舞的占 , 唱歌的比跳舞的多占学生总数的几 分之几 ? 3 5 1 9 5 12 + 1 5 ( )+( 1 12 + 4 5 ) 1 7 + 1 11 + 10 11 5 6 － 1 12 － 5 12 简便计算 整数加法交换律、结合律对 分数加法同样适用 。 在计算分数加、减法时，可 以根据题目的特征，灵活、 合理地选择简便方法． 在一次数学考试中 ,19 名学生 的得分如下 : 80 100 60 80 70 90 80 70 80 70 90 80 90 60 80 90 80 表示把单位 “ 1 ” 平均分成 5 份，取其中 2 份。还表示把 2 平均分成 5 份，取其中 1 份。 表示 2 个 。 表示 2 除以 5 的商。 （分数的意义） 一个物体、一些物体等都可以看作一个整体，把这个整体平均分成若干份，这样的一份或几份都可以用分数来表示。 分数的意义 单位“ 1” 表示： 一个物体、一些物体等都可以看作一个整体，一个整体可以用自然数 1 来表示，通常把它叫做“ 1” 。 分数单位表示： 把单位“ 1” 平均分成若干份，表示其中一份的数叫分数单位。 单位 “ 1 ” 与分数单位的区别 1. 表示把单位“ 1” 平均分成 5 份，取其中 3 份的分数是（ ），它的分数单位是（ ），再添上（ ）个这样的分数单位就是单位“ 1” 。 2. 里面有（ ）个 。 （ ）里面有 3 个 。 3 个 是（ ）。 3. 比比两条线段哪个长？ 1 3 1 4 4. 写出数轴上点 A 、点 B 、点 C 、点 D 表示的分数 5. 请在一条数轴上表示下列分数： 分数与除法的关系 工程队修一条 5 千米长的公路， 7 天修完， （ 1 ）平均每天修这条公路的（ —— ）千米； （ 2 ）平均每千米要修（ —— ）天； （ 3 ）平均每天修的占这条公路的（ —— ）。 工程队修一条 5 千米长的公路， 7 天修完， （ 1 ）平均每 天 修这条公路的（ —— ） 千米 ； 总千米 ÷ 总天数 = 每份数 5 ÷ 7 = （千米） 工程队修一条 5 千米长的公路， 7 天修完， （ 2 ）平均每 千米 要修（ —— ） 天 ； 总天数 ÷ 总千米 = 每份数 7 ÷ 5 = （天） 1 工程队修一条 5 千米长的公路， 7 天修完， （ 3 ）平均 每天 修的占 这条公路 的（ —— ）。 1 ÷ 7 = 工程队修一条 5 千米长的公路， 7 天修完， （ 1 ）平均每天修这条公路的（ ）千米； （ 2 ）平均每千米要修（ ）天； （ 3 ）平均每天修的占这条公路的（ ）。 1 （ 4 ）把 4 米长的钢筋平均截成 5 段， 每 段 长（ ） 米 ？ 总米数 ÷ 总段数 = 每份数 4 ÷ 5 = （米） 每段 是钢筋 全长 的（ —— ） 1 ÷ 5 = （ 5 ）一个班有学生 50 人，其中 13 人被评为 “ 三好学生 ” 。 “ 三好学生 ” 占 全班人数 的（ —— ）。 13 ÷ 50 = 小结：分数与除法的关系 分数可以表示整数除法的商，在表示整数除法时，要用除数作分母，用被除数作分子。 用关系式表示： 被除数 ÷ 除数 = ———— 用字母可以表示成： a÷b = —— 因为除数不能等于 “ 0 ” ，所以 b 也不能等于 “ 0 ” 。 被除数 除数 a b 分数与除法是有区别的。除法是一种运算，它有运算符号，是一个算式；而分数是一个 “ 数 ” ，当它在除法算式中的时候，它可以表示除法算式的结果。 小结： 当一个量不能用整数个计量单位来表示时，可以用分数来表示。即分数可以表示一个量，分数还可以表示两个量之间的关系。 用分数表示下列除法算式的商。 6÷7= 11÷9= 15÷17= a÷b = 下图是长方形，它的面积是 5 平方厘米。请你用阴影表示出 5 8 平方厘米的部分 5 平方厘米 5 平方厘米 5 平方厘米的 1 8 5 平方厘米 1 平方厘米的 5 8 真分数和假分数 意义 特征 真分数 分子比分母小的分数 真分数小于 1 假分数 分子比分母大或分子和分母相等的分数 假分数都大于或等于 1 ４　的分数单位是（　　），去掉（　　）个 这样的分数单位就是最小的合数。 ２ ７ 　　的分数单位是（　　），再添（　　） 个这样的分数单位就是最小的质数。 ７ ８ 在　　中， a 是不为 0 的自然数。 a 5 （真分数？假分数？最小假分数？最大真分数？） 填空 1. 分数的基本性质 分数的分子和分母同时乘或者除以相同的数（ 0 除外），分数的大小不变。这叫做分数的基本性质。 2. 约分 把一个分数化成和它相等，但分子、分母都比较小的分数，叫做约分。 3. 通分 把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。 4. 最简分数 分子、分母只有公因数 1 的分数，叫做最简分数。 分数的基本性质 小结：分数的基本性质 约分 是分数基本性质中的：分子、分母同时除以相同的数（ 0 除外）的体现。 通分 是分数基本性质中的：分子、分母同时乘上相同的数（ 0 除外）的体现。 比较分数的大小 除了用同分母、同分子和通分比较方法外，还可以灵活运用其它的方法。 占单位 “ 1 ” 的一半不够 占单位 “ 1 ” 的一半多 ﹤ 不用通分的方法，比较分数的大小。 因为 ﹥ 所以（ 1 — ） ﹤（ 1— ) ﹤ 将分数化为最简分数，可以将分子分母分别 除以它们的最大公因数， 也可以不断地约分， 直到分子分母 互质 为止。 约分的技巧 分数 的分子加上 8 ，要使分数 大小不变，分母应该（ ）。 0.6=( ) ÷25= 12 （ ） 3 5 或 3÷5 一个分数的分子扩大 20 倍，分母缩小 20 倍，结果如何？ 小数化分数，原来有几位小数就在 1 的后面写几个 0 做分母，把原来的小数去掉小数点作分子； 化成分数后，能约分的要约分。 分小互化 分小互化 分母是 10 、 100 、 1000…… 的分数化小数，可以直接去掉分母，看分母中 1 后面有几个零，就在分子中从最后一位起向左数出几位，点上小数点。 分小互化 分母不是 10 、 100 、 1000… … 的分数化小数，要用分母去除分子；除不尽的，可以根据需要按四舍五入法保留几位小数。 1 2 1 4 2 5 3 4 1 5 1 8 4 5 3 5 3 8 5 8 7 8 1 20 1 16 3 16 5 16 7 16 1 25 1 50 1 40 把下面的分数化成小数， 并且记住这些结果。 3 2 3 1 20 9 5 8 3 3.025 0.16 0.15 0.2222…… 0.6 3.125 0.375 3 20 0.16 3.025 2 9 3 5 3 1 8 ‹ ‹ ‹ ‹ ‹ ‹ 0.375 把下面各数按从小到大的顺序排列起来。 在（ ）里填上合适的分数 50 厘米 = （ ）米 250 克 = （ ）吨 45 分 = （ ）时 400 米 = （ ）千米 600 毫米 = （ — ）米 40 厘米 = （ — ）米 15 秒 = （ — ）分 2500 平方米 = （ — ）公顷 50 100 1 2 1 4 3 4 2 5 1 1 4 4 3 2 5 5 第五单元 图形变换 图形变换的复习 、注重整体把握教材 已学的知识 二年级： 初步感知生活中的轴对称、平移和旋转现象。 初步认识轴对称图形，能在方格纸上画简单的轴对称图 形和沿水平或垂直方向画平移后的图形。 现学的知识 五年级： 进一步认识轴对称，掌握图形成轴对称的特征和性质。 能 在方格纸上画出一个图形的轴对称图形。 进一步认识旋转，能在方格纸上把简单图形旋转 90° 。 初步学会用平移、对称和旋转的方法设计图案。 将学知识 六年级： 圆的对称性。 二、注重知识的把握 意义 性质 特征 轴对称 把一个图形沿着一条直线折叠，如果它能够与另一个图形重合，那么这两个图形成轴对称。这条直线就是对称轴。 对称点到对称轴的距离相等。 沿对称轴对折，对称点、对称线段、对称角度重合。 旋转 物体绕着某一点或轴运动，这种运动现象称为旋转。 图形绕着某一点旋转一定的度数，图形的对称点、对称线段都旋转相应的度数，对应点到旋转点的距离相等，对应的线段、对应的角都相等。 图形旋转后，形状、大小都没有发生变化，只是位置变化了。 平移 对应点所连接的线段平行且相等。 旋转三要素：旋转点（或旋转中心）、旋转方向、旋转角度 注意意义的区别 轴对称是沿着一条直线对折后，两个图形能够完全重合；而轴对称图形是指一个图形沿着一条直线对折后，图形的两部分之间能够完全重合。 轴对称图形是指一个图形，而大小形状完全相同的两个图形才能成轴对称。 （ ） √ （ ） × 成轴对称的两个图形，对称轴只有一条。轴对称图形可以有一条、多条或无数条对称轴。 下列图形中对称轴最多的是（ ） A ：角 B ：等边三角形 C ：线段 D ：正方形 D 3 90° 180° 三、画法 （一）一个图形的轴对称图形的画法 1 、 定： 确定所给图形的关键点，如：图形定点，相交 点，端点。 2 、 数 （或量）：数出或量出图形的关键点到对称轴的距离。 3 、 找 （或量）：在对称轴另一侧找出这些点的对称点。 4 、 连 ：按所给图形的形状连接各对称点。 （二）简单图形旋转 90° 的画法 1. 找出图形的关键点或线段。 2. 借助三角板（或量角器）作原图形线段或关键点与旋转中心所在线段的垂线。 3. 在所做垂线上量出与原线段相等的长度（即找出原图关键点的对应点）。 4. 顺次连接所画出的对应点。 （ 1 ）画出图①的全部对称轴。 （ 2 ）画出图②向上平移 3 格后的图形。 图① 图② A O B （ 3 ）画出绕点 O ，顺时针旋转 90 后的图形。 A O B A' A O B A' A O B A' B' A O B A' B' 四、注重空间观念的训练 （图一）三角形绕点 O （ ）时针旋转了（ ）度。 （图二）三角形 绕点 O （ ）时针旋转了（ ）度。 逆 90 顺 90 旋转不改变图形的 形状 、 大小 ，只改变图形的 位置 。 图（二） o 图（一） o 第六单元 分数的加法和减法 分数的加法和减法 分数加减法的简算 异分母分数加减法 同分母分数连减 同分母分数连加 同分母分数加减法 分数加减混合运算 异分母分数连加 异分母分数连减 同分母分数相加、减，分母不变，只把分子相加减。 1. 同分母分数加减法 （ 1 ）同分母分数加法的意义及计算方法 （ 2 ）同分母分数减法的意义及计算方法 （ 3 ）同分母分数连加、连减 异分母分数加减法，先通分，转化为同分母分数进行计算。 2. 异分母分数加减法 （ 1 ）异分母分数加法 （ 2 ）异分母分数减法 （ 3 ）分数加减法混合运算 a. 不带括号的分数加减法混合运算 b. 带括号的分数加减法混合运算 加法的运算定律和减法的性质同样适应于分数中的计算。 2 7 + 3 7 3 8 + 1 8 5 12 - 3 12 4 9 - 2 9 25 36 - 17 36 - 5 36 9 11 - 1. 口算 - 7 11 2 11 注意化简和简算 2. 计算 异分母分数加减法，先通分，转化为同分母分数进行计算。 加法的运算定律和减法的性质同样适应于分数中的计算。 1 2 + 1 3 1 3 + 1 7 1 5 - 1 8 1 9 - 1 16 先计算下面各题，想一想怎样计算比较快？ 用字母表示为： 1 a ± 1 b = b ± a ab a 、 b 均不为 0 1 2 1 4 1 8 1 16 1 32 + + + + 1 32 1 4 1 8 1 16 1 2 1 2 1 4 1 8 1 16 1 32 + + + + 拆项法： 1 2 = 1 - + 1 2 - 1 4 + 1 4 - 1 8 + 1 8 - + 1 16 - 1 32 1 16 = = 1 1 32 - 31 32 学校图书馆有故事书占图书总数的 ， 工具书占总数的 ， 剩下的是科技书，科技书占总数的 几分之几？ 1- - = - - = 答：科技书占总数的 。 在圆圈内填上适当的分数，使每行、每列的三个数加起来的和都等于 1 。 人教版义务教育课程标准实验教科书 《 数学 》 统计复习建议 统计图表的复习 （一）创设情境：出示三个统计表 表一 五（ 1 ）班学生爱吃食物人数统计表 食物类别 肉禽类 鱼虾类 蔬菜类 合计 人数 18 20 7 45 表二 光明小学四年级同学喜欢各种玩具的人数统计表 玩具名称 小汽车 洋娃娃 跳棋 拼图 男生人数 22 5 15 18 女生人数 8 24 17 14 表三 光明小学一 ---- 六年级喜欢看科普读物人数统计表 年级 一 二 三 四 五 六 人数 20 26 32 47 68 83 提问： 1. 如果将上面的三组数据用统计图的形式表 示，你会分别绘制成什么统计图？为什么？ 2. 这些统计图有什么特点？ 表一 五（ 1 ）班学生爱吃食物人数统计表 食物类别 肉禽类 鱼虾类 蔬菜类 合计 人数 18 20 7 45 表二 光明小学四年级同学喜欢各种玩具的人数统计表 玩具名称 小汽车 洋娃娃 跳棋 拼图 男生人数 22 5 15 18 女生人数 8 24 17 14 表一： 单式条形统计图 表二： 复式条形统计图 表三： 单式折线统计图 表三 光明小学一 ---- 六年级喜欢看科普读物人数统计表 年级 一 二 三 四 五 六 人数 20 26 32 47 68 83 条形统计图 折线统计图 特点 用一个单位长度表示一定的数量 用直条的长短表 示数量的多少。 用折线起伏表示数量 的增减变化。 作用 从图中能清楚地 看出各数量的多 少，便于相互比 较。 从中能清楚地看出数量 的增减变化情况，也能 看出数量的多少。 例如：关于甲、乙两地月平均气温的 情况用复式折线统计图表示。 复式折线统计图的特点： 便于比较两种数据的变化趋势和差异性。 例如：关于国庆 60 周年与 50 周年 阅兵式方阵数量统计图。 复式条形统计图的特点： 便于比较不同组之间的同类数据。 运用知识解决问题 （二） 1. 选择 （ 1 ）心脏科要把病人的血压变化情况绘制成统计图，最佳选择是（ ） A 条形统计图 B 折线统计图 （ 2 ）要表示某校各班向灾区捐款情况，选用（ ）比较合适。 A 条形统计图 B 折线统计图 2. 动手操作 （ 1 ）如果你是世界环保组织成员，想呼吁大家关注碳排 放量，让大家强烈地感受到一定要降低碳排放量， 你将选择 （ 折线 ） 统计图来表达。 理由是： 突出空气中碳的排放量越来越高的发展趋势。 （ 2 ）绘制统计图 2000-2008 年中国碳排放量统计表 年份 2000 2002 2004 2006 2008 碳排放量（百万吨） 3000 3500 5200 5900 6500 绘制的是我国的碳排放量的折线统计图， 修改的是统计图的名称和图例 （ 3 ）绘制、修改、完善统计图 填空 1 . 把 42 分解质因数是（ ） 。 2 . 能同时被 2 、 5 、 3 整除的最小 三位数是（ ）。 3 .10 以内质数的乘积是（ ）。 4. 从 1 — 9 的自然数中， ( ) 和 （ ）是相邻的两个合数； ( ) 和（ ）是相邻的两个 质数。 用铁丝围成长、宽、高分别是 6 分米、 4 分米、 3 分米的长方 体模型三个，至少需要多少分 米铁丝？ 学校组织郊游，可咱班还有一个同学没来，得赶紧给他打电话呀。 我知道他家电话号码。左起第 1 位数是最小的质数 ，第 2 和 5 位数是 10 以内 3 的最大倍数，第 3 ， 4 位是最小的合数，第 6 位是 10 以内最大的质数。最后一位是 10 以内最大的合数。 小朋友，你知道那个同学的电话号码了吗？ 幼儿园买来一些糖果， 第一次吃了它的 , 第二次比第一次少吃 了这些糖果的 , 两次一共吃了这些糖果 的几分之几？ 1 5 1 6 一块长方体石料，体积是 64 立方分米， 已知石料的长是 8 分米，宽是 4 分米。 石料的高是多少分米？（用方程解） 某家超市一分店、二分店销售饮料 情况如下表。 根据表中数据，制成折线统计图， 并回答后面的问题。 ( 1 ) 两个分店销售额最高的是（ ） . ( 2 ）一分店从（ ）月到（ ）月 销售额增长得最快。 ( 3 ）二分店从（ ）月到（ ）月 销售额增长得最快。