人教版五年级下册分数的意义与性质知识点及练习题+六年级下册第二单元《圆柱与圆锥》知识点整理 7页

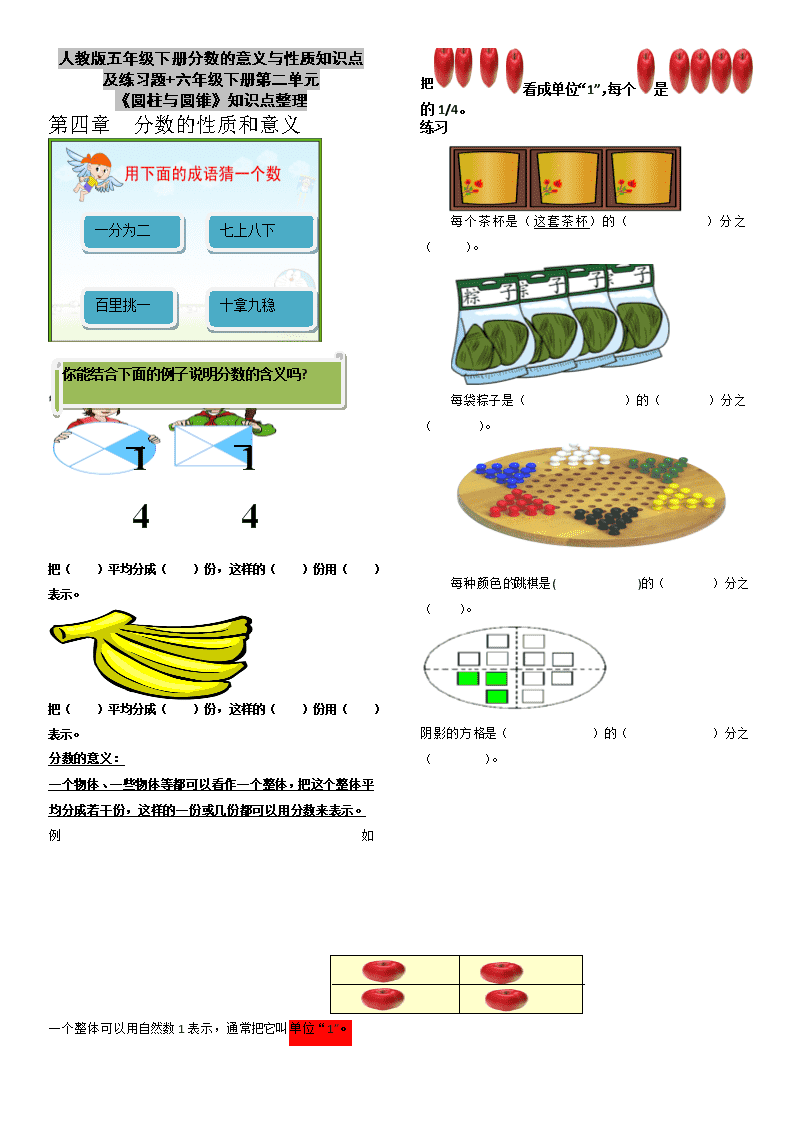
人教版五年级下册分数的意义与性质知识点 及练习题+六年级下册第二单元 《圆柱与圆锥》知识点整理 第四章 分数的性质和意义 1 4 1 4 把（ ）平均分成（ ）份，这样的（ ）份用（ ）表示。 把（ ）平均分成（ ）份，这样的（ ）份用（ ）表示。 分数的意义： 一个物体、一些物体等都可以看作一个整体，把这个整体平均分成若干份， 这样的一份或几份都可以用分数来表示。 例 如 一个整体可以用自然数 1 表示，通常把它叫单位“1”。 把 看 成 单 位 “ 1” ， 每 个 是 的 1/4。 练习 每个茶杯是（这套茶杯）的（ ）分之（ ）。 每袋粽子是（ ）的（ ）分之 （ ）。 每种颜色的跳棋是( )的（ ）分之 （ ）。 阴影的方格是（ ）的（ ）分之 （ ）。 一分为二 七上八下 百里挑一 十拿九稳 你能结合下面的例子说明分数的含义吗? 二 分数单位 把单位“1”平均分成若干份，表示其中一份的数叫分数单位。例如 （ ）的分数单位是（ ）,（ ）的分数单位 是（ ），（ ）的分数单位是（ ）。 三 分数与除法 思考 1、 把三个苹果平均分给 2 个人，每个人分几个？ 2、 把 1 个苹果平均分给 2 个人，每个人分几个？ 3、 把 3 块饼平均分给 5 个小朋友，每人分得多少块？ 3÷5= （块） 你发现分数与除法有什么关系？ 被除数相当于分数的分子，除数相当于分数的分母。被除 数÷除数= 如果用字母 a 表示被除数，b 表示除数，那用字母表示分 数与除法的关系为 a÷b= （ ） 想 一下 b 有什么特点？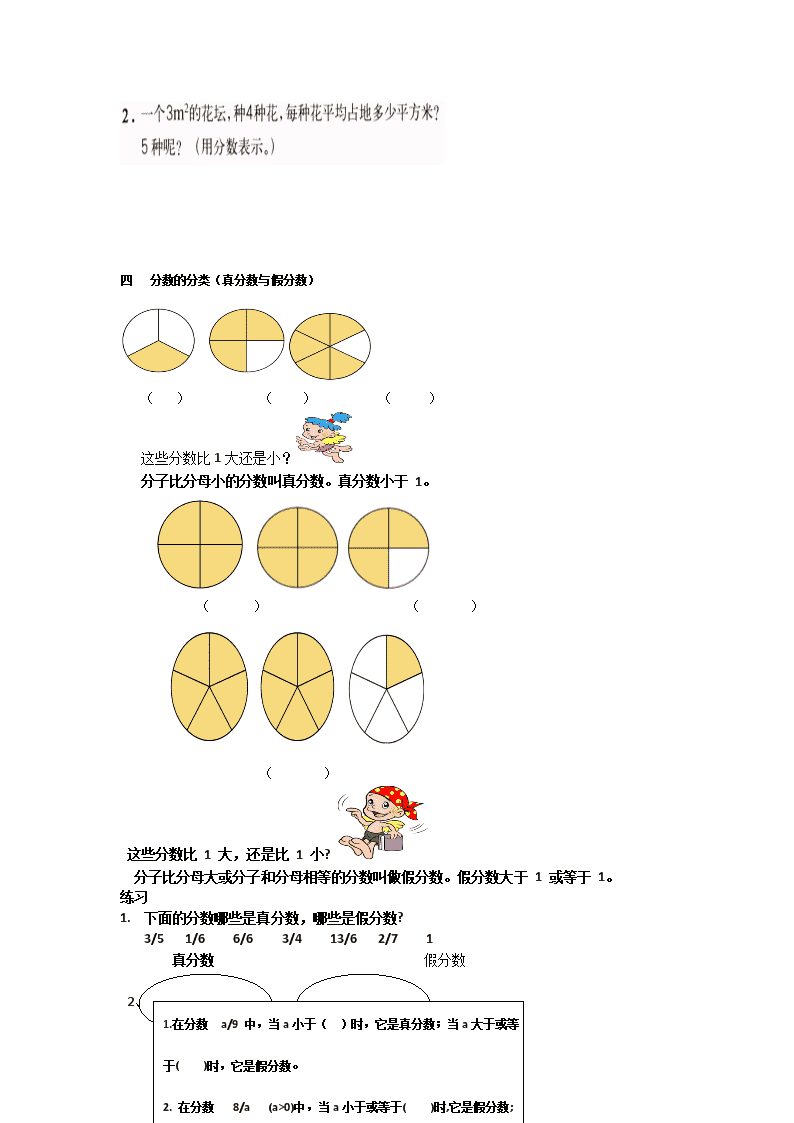 被除数÷除数=被除数/除数 用字母表示分数与除法的关系： 四 分数的分类（真分数与假分数） （ ） （ ） （ ） 这些分数比 1 大还是小？ 分子比分母小的分数叫真分数。真分数小于 1。 （ ） （ ） （ ） 这些分数比 1 大，还是比 1 小? 分子比分母大或分子和分母相等的分数叫做假分数。假分数大于 1 或等于 1。 练习 1. 下面的分数哪些是真分数，哪些是假分数? 3/5 1/6 6/6 3/4 13/6 2/7 1 真分数 假分数 2、 1.在分数 a/9 中，当 a 小于（ ）时，它是真分数；当 a 大于或等于( )时， 它是假分数。 2. 在分数 8/a (a>0)中，当 a 小于或等于( )时,它是假分数; 当 a 大于 3、(1)写出分母是 7 的所有真分数。 (2)写出分子是 7 的所有假分数 。 4、下面的说法对吗? 为什么? (1)昨天妈妈买了 1 个西瓜，我一口气吃了 5/4 个。 (2)爷爷把菜地的 2/5 种了西红柿， 3/5 种了茄子， 1/5 种了辣椒。 (3)这块巧克力 我吃了 1/6，表哥吃了 5/6 。 一课一练 1、 单位一不仅可以表述一个东西，一个计量单位，也可以表示为由一些物体组成的（ ）， 如一块田，一班学生，一堆沙子。 2、 把全班同学平均分成 5 个小组，其中两个小组占全班人数的（ ），这里的单位一是 （ ）。 3、 把 5 米长的绳子平均分成 8 段，每段长多少米？每段占绳子长度的几分之几？ 4、 把 3 千克糖平均分成 5 分，每份是 3 千克糖的几分之几？每份有多少千克？ 5、 把一个苹果平均分成 6 份，其中的 3 份是（ ）米? 6、一班学生有 28 人，二班有 23 人，一班人数占一二班总人数的（ ），二班是一班 人数的（ ），一班是二班的（ ）。 7、要使 x/9 假分数，x/10 是真分数，x 应该是多少？ 8、分数单位是 1/5 的真分数有哪些？最小的假分数是？ 9、9 个 1/10 是（ ），它比 1（ ），是（ ）分数。8 个 1/5 是（ ），它比 1（ ）， 是（ ）分数。 10 、1=（）/1=( )/3=4/( )=8/( ) 11 、根据下面的条件，确定 m 的值 m/7 是真分数，m= m/7 是假分数，m= m/7 是最小的假分数，m= m/7=0,m= m/7 是整数，m 满足什么条件 12、写出结果（用分数表示） 8÷10= 4÷17= 2÷9= 15÷8= 22÷12= 六年级下册第二单元《圆柱与圆锥》知 识点整理 六年级下册第二单元《圆柱与圆锥》知识点整理 第二单元：圆柱与圆锥 一．圆柱 1、圆柱的形成：圆柱是以长方形的一边为轴旋转而得到的；圆柱也可以由长方 形卷曲而得到。 2、圆柱各部分的名称：圆柱的的两个圆面叫做底面（又分上底和下底）；周围的 面叫做侧面；两个底面之间的距离叫做高（高有无数条他们的数值是相等的）。 3、圆柱的侧面展开图： a 沿着高展开,展开图形是长方形，长方形的长等于圆柱底面的周长，长方形的 宽等于圆柱的高，当底面周长和高相等时（h=2πR），侧面沿高展开后是一个正 方形，展开图形为正方形。 b. 不沿着高展开，展开图形是平行四边形或不规则图形。 C.无论如何展开都得不到梯形. 侧面积＝底面周长×高 S 侧=Ch=πd×h =2πr×h 4、圆柱的表面积：圆柱表面的面积，叫做这个圆柱的表面积。 圆柱的表面积＝2×底面积＋侧面积，即 S 表=S 侧+S 底×2 = 2πr×h + 2×πr2 （实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，都要 用进一法） 圆柱的体积：圆柱所占空间的大小，叫做这个圆柱的体积。 圆柱切拼成近似的长方体，分的份数越多，拼成的图形越接近长方体。长方体的 底面积等于圆柱的底面积，长方体的高等于圆柱的高。 长方体的体积=底面积×高 圆柱体积=底面积×高 V 柱＝S h =πr2 h h =V 柱÷S=V 柱÷(πr2) S=V 柱÷h 5、.圆柱的切割： a.横切：切面是圆，表面积增加 2 倍底面积，即 S 增=2πr2 b.竖切（过直径）：切面是长方形（如果 h=2R，切面为正方形），该长方形的长 是圆柱的高，宽是圆柱的底面直径，表面积增加两个长方形的面积，即 S 增=4rh 考试常见题型： a 已知圆柱的底面积和高，求圆柱的侧面积，表面积，体积，底面周长 b 已知圆柱的底面周长和高，求圆柱的侧面积，表面积，体积，底面积 c 已知圆柱的底面周长和体积，求圆柱的侧面积，表面积，高，底面积 d 已知圆柱的底面面积和高，求圆柱的侧面积，表面积，体积 e 已知圆柱的侧面积和高，求圆柱的底面半径，表面积，体积，底面积 以上几种常见题型的解题方法，通常是求出圆柱的底面半径和高，再根据圆柱的 相关计算公式进行计算。 常见的圆柱解决问题： ①、压路机压过路面面积、烟囱、教学楼里的支撑柱、通风管、出水管（求侧面 积）； ②、压路机压过路面长度（求底面周长）； ②、水桶铁皮（求侧面积和一个底面积）； ④鱼缸、厨师帽（求侧面积和一个底面积）； V 钢管=（πR2﹣πr2）×h 二、圆锥 1、圆锥的形成：圆锥是以直角三角形的一直角边为轴旋转而得到的。圆锥也可 以由扇形卷曲而得到。 2、圆锥各部分的名称： 圆锥只有一个底面，底面是个圆，圆锥的侧面是个曲面，把圆锥的侧面展开得到 一个扇形。 从圆锥的顶点到底面圆心的距离是圆锥的高，圆锥只有一条高。（测量圆锥的高： 先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板 和底面之间的距离。） 3、圆锥的体积： 圆锥的体积等于与它等底等高的圆柱体积的三分之一 V 锥= ×底面积×高＝ S h＝ πr2 h 圆锥的高=圆锥体积×3÷底面积 h =3 V 锥÷S = 3 V 锥÷(πr2) 圆锥的底面积=圆锥体积×3÷高 S= 3 V 锥÷h 4.圆锥的切割： a.横切：切面是圆 b.竖切（过顶点和直径）：切面是等腰三角形，该等腰三角形的高是圆锥的高， 底是圆锥的底面直径，表面积增加两个等腰三角形的面积，即 S 增=2Rh 考试常见题型： a 已知圆锥的底面积和高，求体积 b 已知圆锥的底面周长和高，求圆锥的体积，底面积 c 已知圆锥的底面周长和体积，求圆锥的高，底面积 以上几种常见题型的解题方法，通常是求出圆锥的底面半径和高，再根据圆柱的 相关计算公式进行计算。 三、圆柱和圆锥的关系 1．圆柱的特征：一个侧面、两个底面、无数条高且侧面沿高展开图是长形。 2．圆锥的特征：一个侧面、一个底面、一个顶点、一条高且侧面展开图是扇形。 圆柱与圆锥等底等高，圆柱的体积是圆锥的 3 倍。 圆柱与圆锥等底等体积，圆锥的高是圆柱高的 3 倍。 圆柱与圆锥等高等体积，圆锥的底面积（注意：是底面积而不是底面半径）是圆 柱的 3 倍。 圆柱体积比等底等高圆锥体积多 2 倍。 圆锥体积比等底等高圆柱体积少。 （1）等底等高：V 锥:V 柱＝1:3 （2）等底等体积：h 锥:h 柱＝3:1 （3）等高等体积：S 锥:S 柱＝3:1 题型总结： 高不变半径扩大缩小 n 倍，直径、底面周长、侧面积扩大缩小 n 倍，底面积、体 积扩大缩小 n2 倍。 半径不变高扩大缩小 n 倍，侧面积、体积扩大缩小 n 倍 削成最大体积的问题： 正方体里削出最大的圆柱圆锥：圆柱圆锥的高和底面直径等于正方体棱长 长方体里削出最大的圆柱圆锥：圆柱圆锥底面直径等于宽（宽﹥高）圆柱圆锥高 等于长方体高 浸水体积问题：水面上升部分的体积就是浸入水中物品的体积，等于盛水容积的 底面积乘以上升的高度。 等体积转换问题：一圆柱融化后做成圆锥，或圆柱中的溶液倒入圆锥，都是体积 不变的问题，注意不要乘以 1/3 。