六年级上册数学教案- 比 3 比的应用 人教版 3页

思明区“新基础教育”研究教学设计 学校 设计者 授课日期 章节 人教版《义务教育课程标准实验教科书·数学》六年级上册P49-51。‎ 年级 六年级 学科 数学 课题 ‎《比的应用》‎ 课型 解决问题 教学 目标 ‎  1．能在实例的分析中理解按比分配的实际意义。‎ ‎    2．初步掌握按比分配的解题方法，运用所学知识解决按比分配的实际问题。‎ ‎    3．通过贴近学生生活的实例学习，在观察、研讨、交流中让学生感受到数学学习和活动的乐趣。‎ 重点 难点 重点：理解按比分配的意义，能运用比的意义解决按比分配的实际问题。‎ 难点：自主探索解决按比分配的实际问题的策略，能运用数形结合的方法解决按比分配的实际问题。‎ 教材 分析 ‎“比的应用”实际就是我们所熟知的“按比分配”知识，在小学数学中，“比的应用”主要有两个内容，即“比例尺”和“按比分配”，比例尺与比例的知识属于六年级下册内容，按“比例分配”是学习下册内容的一个重要知识基础。所谓“按比分配”就是把一个数量按照一定的比进行分配。它是旧知识“平均分”问题的一个发展，我们习惯把按“1： 1”分，称为平均分；把按“X：Y”这种称为按比分配，显然，平均分是按比分配的特例。按比分配问题两种不同解法：一是把“比”看作分得的份数，用先求出每一份的方法来解答；二是把比化为分数，用分数问题来解答。针对学生已有的知识基础，本节课采用第一种方法来展开教学。‎ 学情 分析 本节教学内容是在学生学习了比的意义、比的基本性质的基础上进行教学的，尤与“平均分”的知识有一个特殊的联系与拓展，在学生此前接触的分东西问题上，主要以“平均分”为基础进行的，但此课很大一个切入点是让学生明白“不平均分”在生活也普遍存在着。在本课设计上，我主要是联系学生的生活实际情景与旧知，来帮助学生把“平均分”与“不平均分——按比例分”联系起来，相信学生理解起来并不会很困难，在此基础上再利用情景让学生学习“按比例分”过程中体会数学的魅力与数学美。‎ 教学 策略 长程两段教学策略 教学 资源 多媒体课件、导学单 教学 媒体 课件，实物展台 教学过程设计 教学环节 教师活动 学生活动 设计意图和 活动目标 生活链接 需求激发 谈话：学校买来一些橘子，想要分给五（1）班和五（2）班，1班50人，2班50人，可以怎么分？‎ 考虑：如果1班有50人，2班有40‎ 平均分，也就是按班级平均分成2份 按人数分 借助不同情境的对比，体验平均分和不能平均分的生活事实。感受 人，如果还按班级分合理吗？你觉得应用按什么分比较合理？‎ 归纳总结：比在实际生产和日常生活中有着广泛的应用，今天我们就一起来学习比的应用。（板书课题）‎ 按一定的比进行分配的必要性，从而走进本节课的学习。‎ 有向开放 自主探究 出示问题一：一张格子纸，红色方格和黄色方格的比是5:3。‎ 分析：由这个比，你知道了什么信息？‎ 画线段图：红：‎ ‎ 黄：‎ 明确：这里存在四个量，一个是红格子的量，一个是黄格子的量，还可以知道总量和相差量。‎ 一放：要求红色格子有几个，可以补充什么条件呢？有几种补法？‎ 一收：从总数处理起 思考：红黄格子总数如果是10格，可以计算红格子数吗？‎ 明确：总数和总份数要有“整数倍”关系。‎ 二放：要求红格子有几格？除了补总量，还可以补充什么条件呢？ ‎ 呈现资源：‎ ‎①补充部分量 ‎②补充相差量 追问：这里填的数据必须是几的倍数？‎ 尝试研究已知格子总数，求红格子数的情况。‎ ‎1.结合自己补充的题目，动笔算一算。‎ ‎2.聚焦：虽然补充的数据不同，但在解题方法时，有什么相同点？‎ ‎3.快速列式：（1）黄色格子有几格的情况 ‎ （2）黄色格子和红色格子相差几格的情况 ‎ (结合线段图解释）‎ 自主研究已知部分求部分、已知相差求部分的两种情况 学习要求：‎ 1. 请结合条件和问题，画出线段图。‎ 2. 结合线段图，分析解答。‎ 3. 对计算结果进行检验。‎ 交流汇报：‎ 关注检验方法 思考当一份数已知，除了知道红色格子数有几格？还可以知道什么量呢？‎ 汇报：‎ 红色格子有这样的5份，黄色格子有这样的3份，一共有8份，相差2份。‎ 独立思考，尝试补充条件并解决问题。‎ 动笔尝试，注意关注数据的特点。‎ 小组讨论补充的数据要符合什么条件？理由是什么。‎ 尝试动笔计算并检验。‎ 先求一份是多少，再求几份 独立解答并检验 通过开放式的问题促使学生主动思考，打开思维，引导学生从总量、部分量、相差量多角度入手补充条件，并思考数据应具备的特点，把握三种题目中补充条件和数据虽各不相同，但在解决方法上的相同点，沟通新旧知识之间的联系。‎ 方法建构：回顾这三种题目，补充的条件和数据各不相同，但在解决方法上有相同点？‎ 追问：同样是求1份数时，为什么有时候除以5，有时候除以3，有时候又除以2呢？‎ 二收：已知的量要和份数相对应 总数÷总份数=每份数 部分数÷部分的份数=每份数 ‎ 相差数÷相差的份数=每份数 三放：出示问题二：如果已知红黄蓝格子数的比是5:3:2，可以补充什么条件？又能提出什么数学问题？‎ 学生从不同的角度补充条件并解答。‎ 三收：可以从哪些角度补充条件？可以怎样解决这类问题？‎ 选择不同角度补条件并解决，再以四人小组为单位交流各自的方法，并互相检验。‎ 生活应用 拓展提升 ‎1.一个长方形的周长是42厘米，长和宽比是4:3，长和宽各是多长？‎ ‎2.课件呈现生活中的各种情境。‎ 这些事例中按什么样的比分配更合理？‎ 独立解决问题 人人检验纠错 讨论确定按什么比分配更合理。‎ 拓展性变式练习，避免定势思维，关注对应关系，养成解决问题后检验的好习惯。‎ 感受按比分配的合理性，感受比在生活中应用。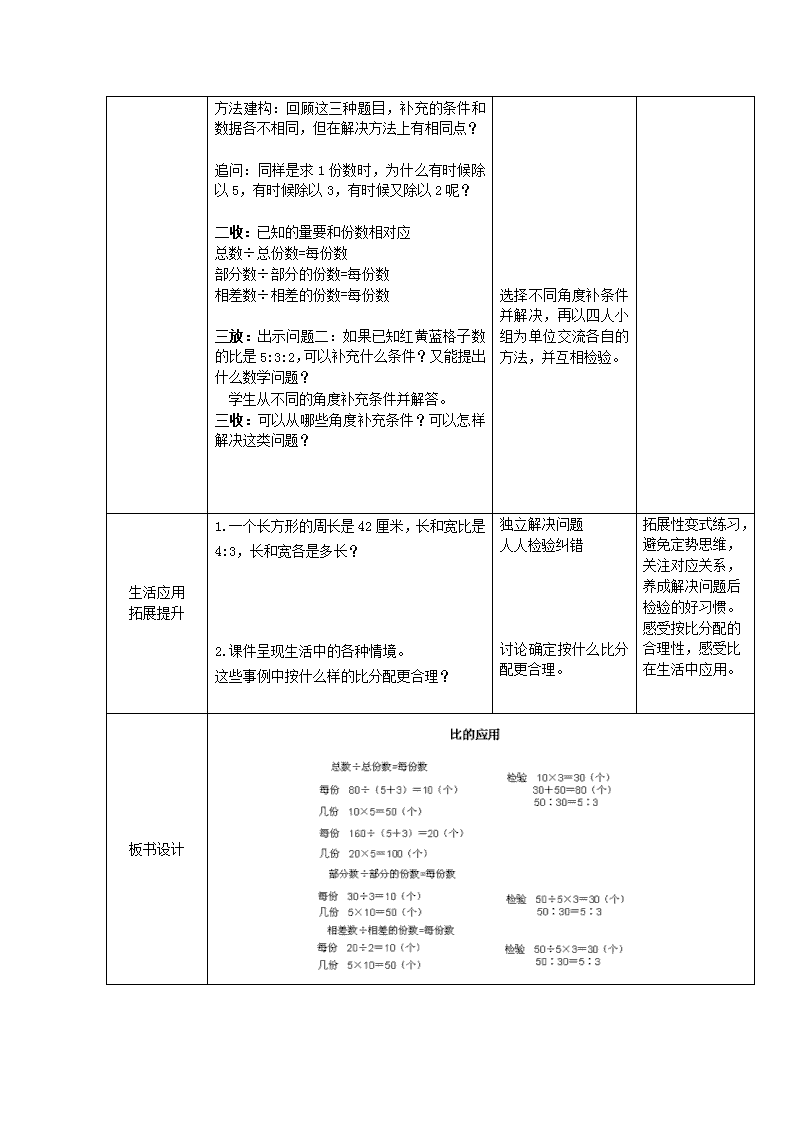‎ 板书设计