六年级数学上册教案-8数与形-人教版 (5) 4页

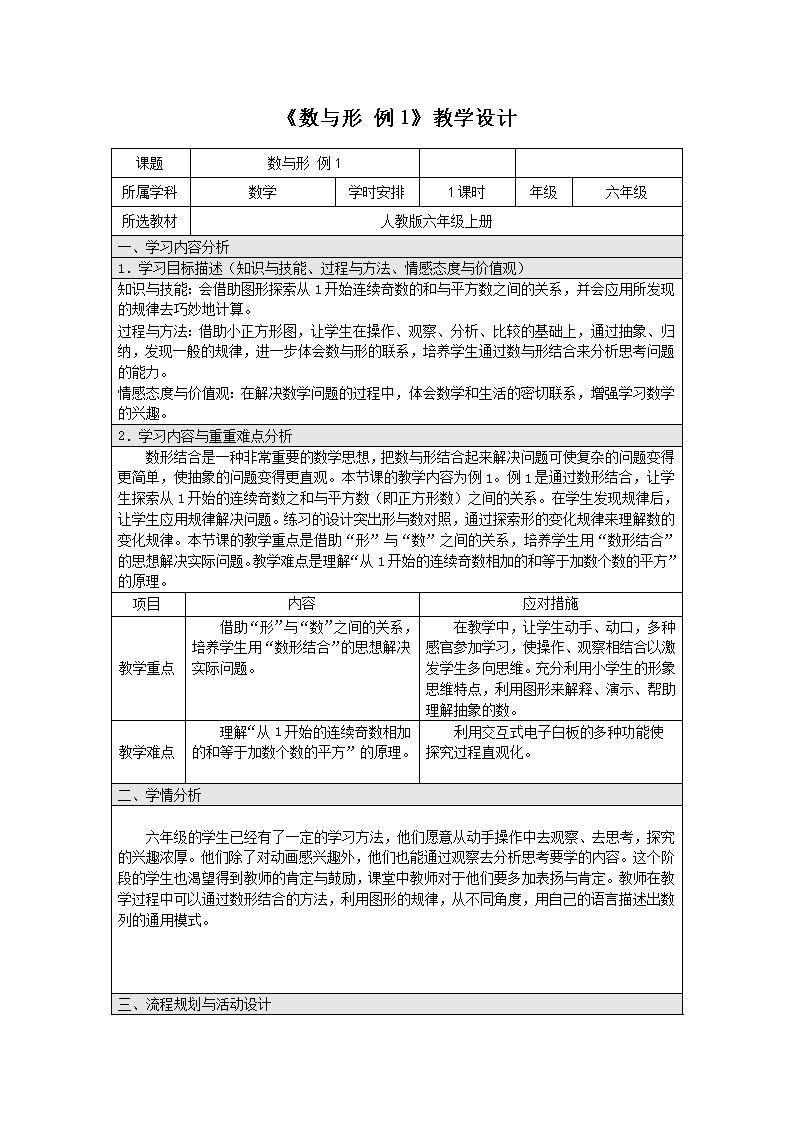
《数与形 例 1》教学设计 课题 数与形 例 1 所属学科 数学 学时安排 1 课时 年级 六年级 所选教材 人教版六年级上册 一、学习内容分析 1．学习目标描述（知识与技能、过程与方法、情感态度与价值观） 知识与技能：会借助图形探索从 1 开始连续奇数的和与平方数之间的关系，并会应用所发现 的规律去巧妙地计算。 过程与方法：借助小正方形图，让学生在操作、观察、分析、比较的基础上，通过抽象、归 纳，发现一般的规律，进一步体会数与形的联系，培养学生通过数与形结合来分析思考问题 的能力。 情感态度与价值观： 在解决数学问题的过程中，体会数学和生活的密切联系，增强学习数 学的兴趣。 2．学习内容与重重难点分析 数形结合是一种非常重要的数学思想，把数与形结合起来解决问题可使复杂的问题变得 更简单，使抽象的问题变得更直观。本节课的教学内容为例 1。例 1 是通过数形结合，让学 生探索从 1 开始的连续奇数之和与平方数（即正方形数）之间的关系。在学生发现规律后， 让学生应用规律解决问题。练习的设计突出形与数对照，通过探索形的变化规律来理解数的 变化规律。本节课的教学重点是借助“形”与“数”之间的关系，培养学生用“数形结合” 的思想解决实际问题。教学难点是理解“从 1 开始的连续奇数相加的和等于加数个数的平方” 的原理。 项目 内容 应对措施 教学重点 借助“形”与“数”之间的关系， 培养学生用“数形结合”的思想解决 实际问题。 在教学中，让学生动手、动口，多种 感官参加学习，使操作、观察相结合以激 发学生多向思维。充分利用小学生的形象 思维特点，利用图形来解释、演示、帮助 理解抽象的数。 教学难点 理解“从 1 开始的连续奇数相加 的和等于加数个数的平方”的原理。 利用交互式电子白板的多种功能使 探究过程直观化。 二、学情分析 六年级的学生已经有了一定的学习方法，他们愿意从动手操作中去观察、去思考，探究 的兴趣浓厚。他们除了对动画感兴趣外，他们也能通过观察去分析思考要学的内容。这个阶 段的学生也渴望得到教师的肯定与鼓励，课堂中教师对于他们要多加表扬与肯定。教师在教 学过程中可以通过数形结合的方法，利用图形的规律，从不同角度，用自己的语言描述出数 列的通用模式。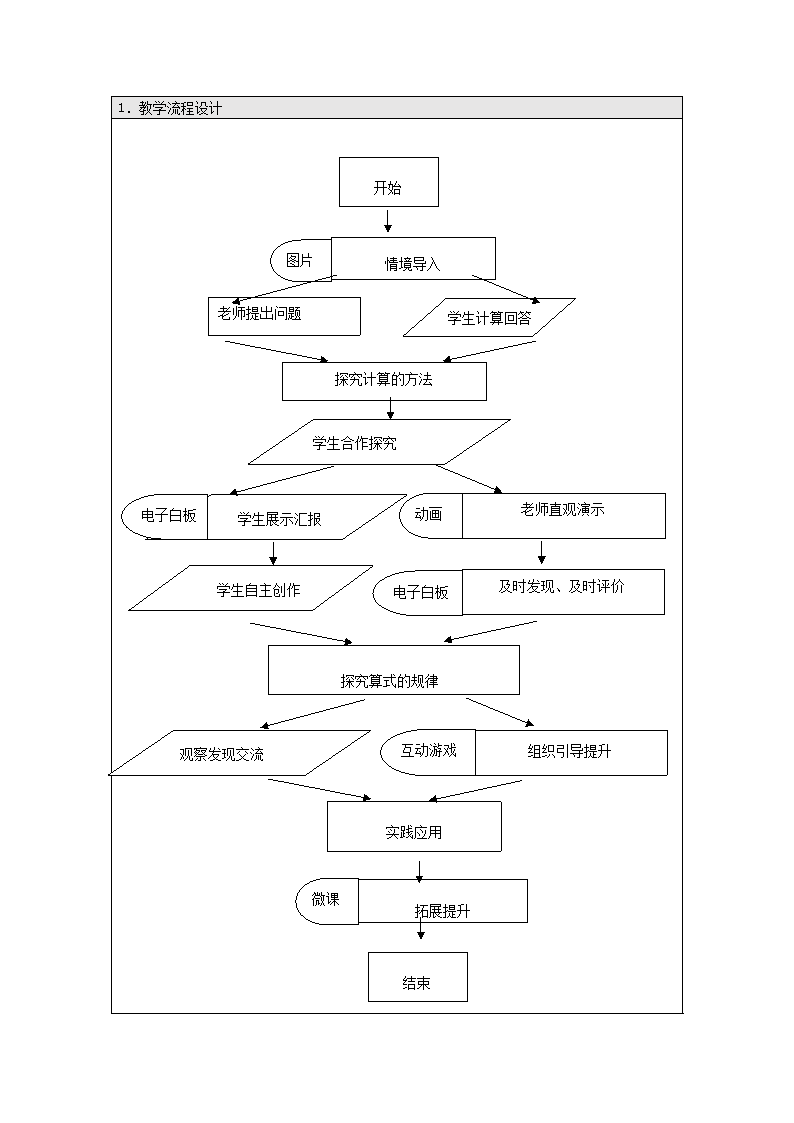 三、流程规划与活动设计 1．教学流程设计 情境导入图片 老师提出问题 学生计算回答 探究计算的方法 学生合作探究 学生展示汇报 学生自主创作 老师直观演示 及时发现、及时评价 动画 电子白板 探究算式的规律 观察发现交流 组织引导提升 实践应用 拓展提升 结束 开始 电子白板 微课 互动游戏 教学环节 教学过程 媒体作用及分析 游戏导入 1.拆礼物盒 拆拆看，礼物盒里有什么？ （学生口算 1+3=，1+3+5=，1＋3＋5＋7=） 观察气球上的数字，你有什么发现？（奇数） 由这些奇数组成的算式，你还能一口气说出结果吗？ 2.揭示课题 师：这节课就进一步来探究这个有趣的问题：如何快速计 算从 1 开始连续奇数相加的和？ 【板书：数与形 从 1 开始连续奇数的和】 （设计意图：引导学生在对比式、冲突式具体情境中发现 问题、提出问题，激发学生的好奇心和求知欲；以问题为 驱动，引发学生积极思考、动手探究、合作交流。） 通过触发动画设计 拆礼物盒的游戏， 激发学生的好奇心 和求知欲。 探究新知 ⒈小组合作，根据算式摆小正方形。 师：我们从最简单的运算入手，请这些不同颜色的小正方 形来帮忙。出示算式 1+3。 小组合作：用 4 个小正方形摆出不同的图形。 思考：怎么拼能更快的算出小正方形的个数？ 手机端投屏展示学生拼图成果。 师：我们继续拼摆：1+3+5。出示已有 1+3 的正方形图。 师：再增加 5 个小正方形，还能拼成更大的正方形吗？ 指名学生上台展示 问：现在拼成了更大的正方形，你能根据图形说出 1+3+5 的结果吗？ （设计意图：学生自主动手用小正方形摆出算式 1+3、 1+3+5，经历了将数转化为形的过程，理解了数与形之间的 联系，感悟到了数形结合、数形对应的数学方法） ⒉根据拼图，探究算法。 师：同学们，让我们回过头来看一看，我们如何计算每个 大正方形中小正方形的个数？ 师：单独一个小正方形，如何用算式来表示它的个数？ 师：要想知道可以摆成几列几行，其实看什么数就行了？ （设计意图：学生在计算每个大正方形所含小正方形的总 个数时，是通过观察、思考，自主发现、获取了 1²、2²、 3²的计算方法的，而不是模仿或教师灌输的，这有利于培 养学生的抽象能力和交流能力。） 3.举例验证，深化理解。 使 用 图 形 拖 拽 功 能，帮助生直观感 知。 利用交互式电子白 板的多种功能使探 究过程直观化。（克 隆、拖动、批注、 动态保存、任意切 换、随意更换笔的 颜色） 师：同学们，我们前面列举了三个算式，观察算式里 加数的个数与它们的和，你有什么猜想？ 这个猜想是否成立，让我们分小组举例来验证。 继续摆，应该在图形外围增加几个小正方形？增加 5 个够不够？（移动图形，发现不够），所以要增加 7 个才 可以。形成的新的大正方形每边有几个小正方形？（ 4 个） 所以算式中是加？（7） ，结果是 4 的平方。接下来请在 小组中继续举例验证。 师：这样的式子能不能写完？可以用…… 表示。 观察这些算式，你有什么发现？预设： ①每增加一个加数，就会得到一个更大的正方形。 ②算式左边的加数的个数与对应的大正方形中每行(或每 列)的小正方形的个数相同； ③等式左边是连续的奇数相加。 师总结：同学们说的都很好，这就是我们今天的发现：从 “1”开始的连续奇数相加，有几个数就可以排成几行几列 的大正方形，和就是几的平方。 （设计意图：运用举例验证法和不完全归纳法，让学生进 一步体验数学规律的普遍意义，增强学生对数学思想方法 的愉悦情感，感受数学的魅力。） 认识形数 师：像 1²、2²、3²这样的数叫平方数，也叫正方形数，想 知道为什么吗？让我们通过一段小短片来了解一下吧！ （设计意图：借助三角形数与正方形数这些特殊的数，让学 生进一步感受数形之间有趣的联系。） 感受数字与图形之 间有趣的联系 数形结合 师：本学期我们还经历过哪些数形结合的例子？阅读名人 名言，体验数形结合是一种非常重要的数学思想。 （设计意图：回忆数形结合思想在以往学习中的应用，感 受数形结合思想的价值。） 课堂总结 出示思维导图总结本课的学习内容。 拓展延伸 运用数形结合的方法，探索从 2 开始连续偶数的和的规律。