六年级下册数学单元测试-3正比例、反比例 冀教版 （含答案） 6页

六年级下册数学单元测试-3。正比例、反比例 一、单选题 1.火箭每秒能飞行 4050 米，6 秒能飞行（ ） A. 23300 米 B. 24300 米 C. 24000 米 D. 34000 米 2.表示 x，y 正比例关系的是 （ ） A. x﹣y=5 B. y=x× C. y+x=20 D. xy=7 3.商一定，被除数与除数（ ）。 A.成正比例 B.成反比例 C.不成比例 4.下面关于正比例和反比例的说法，正确的是（ ）。 A.一个人的年龄和体重成正比例关系。 B.圆柱的底面积一定，体积和高成反比例关系。 C.书的单价一定，购买的钱数与购买数量成正比例关系。 二、判断题 5.每小时劳动报酬一定，总收入与工作时间成正比例。（ ） 6.图上距离与实际距离成正比例。（ ） 7.圆的周长一定，直径和圆周率成反比例。 （ ） 8.煤的数量一定，使用天数与每天的平均用煤量成正比例关系。（ ） 三、填空题 9.路程=________×________；时间=________÷________；速度=________÷________． 10.已知关系式 （x、y≠0），则 y 和 x成________比例。 11.圆柱的底面积一定，体积和高成________比例。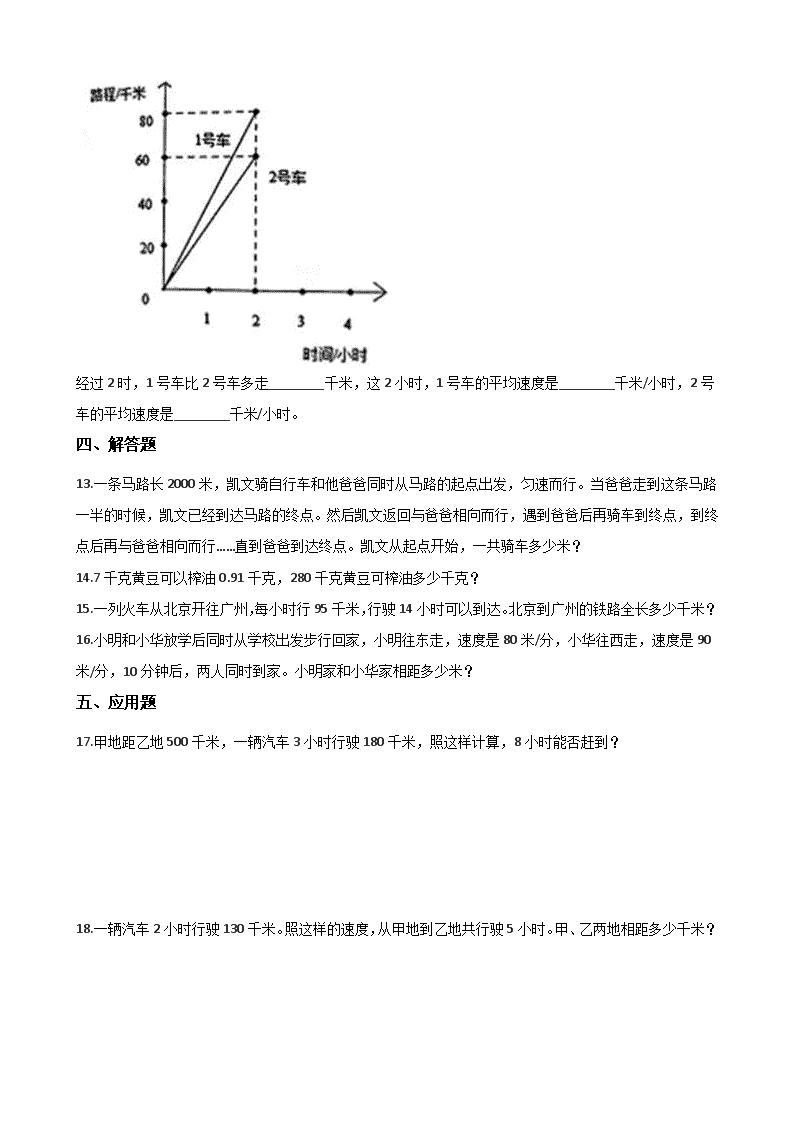 12.下边是 1 号车和 2 号车行驶关系图。 经过 2 时，1 号车比 2 号车多走________千米，这 2 小时，1 号车的平均速度是________千米/小时，2 号 车的平均速度是________千米/小时。 四、解答题 13.一条马路长 2000 米，凯文骑自行车和他爸爸同时从马路的起点出发，匀速而行。当爸爸走到这条马路 一半的时候，凯文已经到达马路的终点。然后凯文返回与爸爸相向而行，遇到爸爸后再骑车到终点，到终 点后再与爸爸相向而行……直到爸爸到达终点。凯文从起点开始，一共骑车多少米？ 14.7 千克黄豆可以榨油 0.91 千克，280 千克黄豆可榨油多少千克？ 15.一列火车从北京开往广州，每小时行 95 千米，行驶 14 小时可以到达。北京到广州的铁路全长多少千米？ 16.小明和小华放学后同时从学校出发步行回家，小明往东走，速度是 80 米/分，小华往西走，速度是 90 米/分，10 分钟后，两人同时到家。小明家和小华家相距多少米？ 五、应用题 17.甲地距乙地 500 千米，一辆汽车 3 小时行驶 180 千米，照这样计算，8 小时能否赶到？ 18.一辆汽车 2 小时行驶 130 千米。照这样的速度，从甲地到乙地共行驶 5 小时。甲、乙两地相距多少千米？ 参考答案 一、单选题 1.【答案】 B 【解析】【解答】4050×6=24300（米） 故答案为：B. 【分析】根据题意可知，已知速度和时间，求路程，用速度×时间=路程，据此解答. 2.【答案】 B 【解析】【解答】如果两个相关联的量 x、y 可以写成 （一定），那么称 x 和 y 成正比例关系。其中 B 选项可以转换为 的形式。 故答案为：B. 【分析】根据两个量成正比例关系的性质，两个量同时扩大或缩小，比值不变。 3.【答案】 A 【解析】【解答】解：被除数÷除数=商，商一定，被除数和除数的商一定，二者成正比例。 故答案为：A。 【分析】根据除法中各部分之间的关系确定被除数与除数的商一定还是乘积一定，如果商一定就成正比 例，如果乘积一定就成反比例。 4.【答案】 C 【解析】【解答】A 选项， 一个人的年龄和体重不成比例。原说法错误 ； B 选项， ， 圆柱的底面积一定，体积和高成正比例关系。原说法错误 ； C 选项， ， 书的单价一定，购买的钱数与购买数量成正比例关系。原说法正确。 故答案为：C。 【分析】两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值 （也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系； 两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两 种量就叫做成反比例的量，他们的关系叫做反比例关系。 二、判断题 5.【答案】 正确 【解析】【解答】每小时工作酬劳=工作总收入÷工作时间，每小时工作酬劳一定，所以总收入与工作时间 成正比例。 故答案为：正确。 【分析】两个量相乘积一定，则这两个量成反比例；两个量相除商一定，则这两个量成正比例。本题即 是据此解答。 6.【答案】 错误 【解析】【解答】解：当比例尺一定时，图上距离与实际距离成正比例。 故答案为：错误。 【分析】比例尺=图上距离：实际距离，所以当比例尺一定时，图上距离与实际距离成正比例。 7.【答案】 错误 【解析】【解答】解：因为圆周率是定值，故原题说法错误. 故答案为：错误. 【分析】根据反比例的定义，如果相关联的两个量比值一定，这两个量就成反比例，本题中有周长和圆周 率是定值，不符合反比例定义，据此判断即可. 8.【答案】 错误 【解析】【解答】 煤的数量一定，使用天数与每天的平均用煤量成反比例关系。 故答案为：错误。 【分析】在本题中用煤数量（一定）=平均每天用煤量×使用天数，积一定，根据反比例关系得出， 使用 天数与每天的平均用煤量成反比例关系。 三、填空题 9.【答案】速度；时间；路程；速度；路程；时间 【解析】【解答】解：路程=速度×时间；时间=路程÷速度；速度=路程÷时间。 故答案为：速度；时间；路程；速度；路程；时间。 【分析】路程=速度×时间；时间=路程÷速度；速度=路程÷时间。 10.【答案】 反 【解析】【解答】解：因为 = ， 所以 xy=18，则 y 与 x 成反比例。 故答案为：反。 【分析】两个量相乘积一定，则这两个量成反比例；两个量相除商一定，则这两个量成正比例。 本题中根据比例的基本性质（在比例中，两个外项之积等于两个内项之积），可得 xy=6×3，再进行判断 即可得出答案。 11.【答案】 正 【解析】【解答】解：体积÷高=圆柱的底面积(一定)，体积和高成正比例. 故答案为：正 【分析】根据圆柱的体积公式判断体积和高的商一定还是积一定，如果商一定就成正比例，如果积一定就 成反比例，否则不成比例. 12.【答案】 20；40；30 【解析】【解答】解：1 号车比 2 号车多走：80-60=20（千米）；1 号车平均速度：80÷2=40（千米/小时）； 2 号车平均速度：60÷2=30（千米/小时）。 故答案为：20；40；30。 【分析】2 小时时，1 号车共行驶 80 千米，2 号车共行驶 60 千米；用减法计算多走的路程，用除法分别计 算每辆车的平均速度。 四、解答题 13.【答案】解：2000×2＝4000(米) 答：凯文从起点开始，一共骑车 4000 米。 【解析】【分析】由题可知，当爸爸走到这条马路一半的时候，凯文已经到达马路的终点，说明凯文骑车 的速度是爸爸的 2 倍，当爸爸到达终点的时候（爸爸走完全程），凯文已经回到了起点（凯文走了两个全 程），由此可求出凯文一共骑车的路程。 14.【答案】 解：设可以榨油 x 千克， 280:x=7:0.91 7x=280×0.91 x=280×0.91÷7 x=36.4 答：280 千克黄豆可以榨油 36.4 千克. 【解析】【分析】黄豆的出油率是不变的，黄豆的重量与榨油的重量成正比例，设出未知数，根据正比例 关系列出比例解答即可. 15.【答案】 95×14=1330（千米） 答： 北京到广州的铁路全长 1330 千米。 【解析】【分析】火车速度×火车行驶时间=北京到广州的铁路全长。 16.【答案】 解：80×10+90×10 =800+900 =1700（米） 答：小明家和小华家相距 1700 米。 【解析】【分析】小明家和小华家的距离=小明家到学校的距离+小华家到学校的距离，小明家到学校的距 离=小明的速度×时间，小华家到学校的距离=小华的速度×时间，据此解题。 五、应用题 17.【答案】 解：180÷3×8， =60×8， =480（千米）； 480＜500； 答：8 小时不能赶到 【解析】【分析】先用 3 小时行驶的路程 180 千米除以 3 小时，求出速度，再用速度乘上 8 小时，求出 8 小时行驶的路程，然后与 500 千米比较即可．先根据速度=路程÷时间，求出不变的速度，再用速度求出 8 小时可以行驶的路程，然后比较求解． 18.【答案】 解：设甲、乙两地相距 x千米.130:2=x:5 2x=5×130 x=325 答：设甲、乙两地相距 325 千米. 【解析】【分析】速度不变，行驶的路程与时间成正比例，设出未知数，根据速度不变列出比例解答即可 求出两地的实际距离.