北师大版七年级数学下册第四章三角形复习课2（共18张PPT）(1) 18页

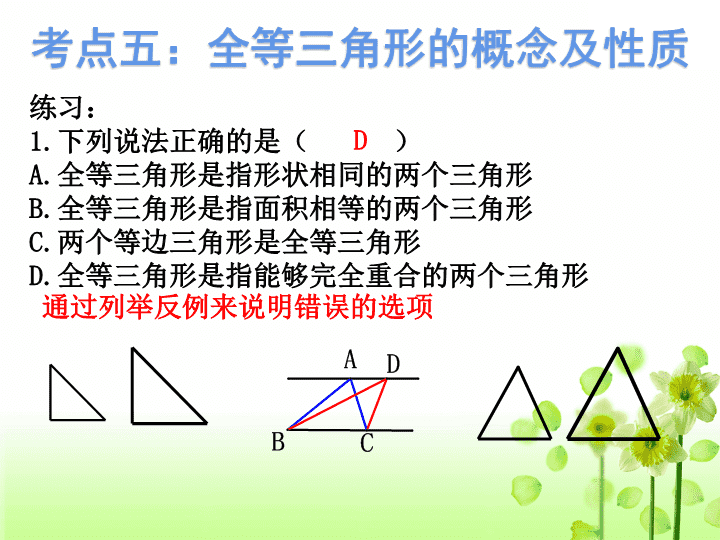
第四章三角形复习课 三角形全等 考点五：全等三角形的概念及性质 知识点： 1. 能够完全 称为全等图形； 2.全等图形的 都相同 ； 3.能够完全 叫做全等三角形； 4.全等三角形的 相等 ， 相等 ，对应中线 ，对应角平分线 ，对应高 . 重合的图形 重合的三角形 形状和大小 对应边 对应角 相等 相等 相等 考点五：全等三角形的概念及性质 练习： 1. 下列说法正确的是（ ） A. 全等三角形是指形状相同的两个三角形 B. 全等三角形是指面积相等的两个三角形 C. 两个等边三角形是全等三角形 D. 全等三角形是指能够完全重合的两个三角形 D 通过列举反例来说明错误的选项 考点五：全等三角形的概念及性质 2. 指出下列各组全等三角形的对应边和对应角 . 考点五：全等三角形的概念及性质 3. 如图，△ ABC≌ △ DEF, 则图中线段相等的对数是（ ） A.3 对 B.4 对 C.5 对 D.6 对 B 4. 如图，△ ABE≌ △ CDF, 则下列结论错误的是（ ） A. AB=CD B. AB//CD C. BE//DF D. BE=CD D 考点六：全等三角形的判定及性质 知识点：全等三角形的判定方法有： SSS SAS ASA AAS 1. 如图，四边形 ABCD 中， AB=BC,AD=CD, 试说明： ∠A=∠C 分析：证明 “ 两角相等 ” 的方法是： （ 1 ）利用角平分线 （ 2 ）利用平行线 （ 3) 同角（或等角）的余角相等 （ 4 ） 同角（或等角）的补角相等 （ 5 ）对顶角相等 （ 6 ）等量代换 （ 7 ）全等三角形的对应角相等（即证明这两角所在的三角形全等） 考点六：全等三角形的判定 （ SSS) 1. 如图，四边形 ABCD 中， AB=BC,AD=CD, 试说明： ∠A=∠C 证明：连接 BD, 在△ ABD 和△ CBD 中 ∴△ ABD ≌△ CBD （ SSS) ∴ ∠A=∠C ( 全等三角形的对应角相等） 总结： 公共边一定是对应边 考点六：全等三角形的判定 （ SSS) 考点六：全等三角形的判定 （ SSS) 2. 如图，已知 AD=BC,OD=OC,O 为 AB 的中点，试说明 ∠C=∠D. 证明： ∵ O 为 AB 的中点 （已知） ∴ OA=OB （中点的定义） 在△ AOD 和△ BOC 中 ∴△ AOD ≌△ BOC （ SSS) ∴ ∠D=∠C ( 全等三角形的对应角相等） 考点六：全等三角形的判定 （ SSS) 3. 如图， AB=CD,BF=DE,E,F 是 AD 上的两点，且 AE=CF. 请你判断 BF 与 DE 的位置关系，并说明理由 . 解： BF//DE 理由： ∵ AE=CF ( 已知） ∴ AE+EF=CF+EF （等式的性质） 即 AF=CE 在△ ABF 和△ CDE 中 ∴△ ABF ≌△ CDE （ SSS) ∴ ∠1=∠2 ( 全等三角形的对应角相等） ∴ BF//DE ( 内错角相等，两直线平行） 1. 如图， AB 与 CD 相交于点 O,O 是 AB 的中点， ∠A=∠B, △ AOC 与△ BOD 全等吗？为什么？ 考点七：全等三角形的判定 （ ASA,AAS) 解： △ AOC 与△ BOD 全等 理由： ∵ O 为 AB 的中点 （已知） ∴ OA=OB （中点的定义） 在△ AOC 和△ BOD 中 ∴△ AOB ≌△ BOD （ ASA) 总结： 对顶角一定是对应角 考点七：全等三角形的判定 （ ASA,AAS) 2. 如图，点 E,A,C 在同一条直线上 ,AB//CD,∠B=∠E, AC=CD, 试说明： BC=ED. 证明： ∵ AB//CD ( 已知） ∴ ∠1=∠ 2 （两直线平行，内错角相等） 在△ ABC 和△ CED 中 ∴△ ABC ≌△ CED （ AAS) ∴ BC=ED ( 全等三角形的对应边相等） 考点八：全等三角形的判定（ SAS) 1. 如图， AB 与 CD 相交于点 E,AE=CE,DE=BE, 试说明： ∠A=∠C. 证明：在△ ABC 和△ CED 中 ∴△ ABC ≌△ CED （ SAS) ∴ ∠A=∠C ( 全等三角形的对应角相等） 2 .如图，OA=OB,OC=OD， ∠D=30 ° ，求∠C的度数. 解： 在△ AOD 和△ BOC 中 ∴△ AOD ≌△ BOC （ SAS) ∴ ∠C=∠D=30 ° ( 全等三角形的对应角相等） 总结： 公共角一定是对应角 考点八：全等三角形的判定（ SAS) 考点八：全等三角形的判定（ SAS) 3. 如图，已知 AB=AD,AC=AE,∠BAE=∠DAC, 试说明 ∠C=∠E. 证明： ∵ ∠BAE=∠DAC ( 已知） ∴ ∠BAE-∠CAE=∠DAC-∠CAE 即 ∠BAC=∠DAE ∴△ ABC ≌△ ADE （ SAS) ∴ ∠C=∠E ( 全等三角形的对应角相等） 在△ ABC 和△ ADE 中 4. 如图，点 C,F 在线段 BE 上 ,BF=EC,∠1=∠2,AC=DF, 试说明 : △ ABC ≌△ DEF 考点八：全等三角形的判定（ SAS) 分析：已知 “ 一边一角 ” ，再找出夹角的另外一组边相等即可 证明： ∵ BF=EC ( 已知） ∴ BF-FC=EC-FC （等式的性质） 即 BC=EF 在△ ABC 和△ DEF 中 ∴△ ABC ≌△ DEF （ SAS) 综合 1. 如图， BD 是 ∠ABC 的平分线， AB=BC, 点 E 在 BD 上，连接 AE,CE, 过点 D 作 DF AE,DG CE, 垂足分别是 F,G. 试说明： (1) △ ABE ≌△ CBE; (2)DF=DG 证明： (1) ∵ BD 是 ∠ABC 的平分线 （已知） ∴ ∠1=∠ 2 （角平分线的定义） 在△ ABE 和△ CBE 中 ∴△ ABE ≌△ CBE （ SAS) 综合 1. 如图， BD 是 ∠ABC 的平分线， AB=BC, 点 E 在 BD 上，连接 AE,CE, 过点 D 作 DF AE,DG CE, 垂足分别是 F,G. 试说明： (1) △ ABE ≌△ CBE; (2)DF=DG 证明： (2) ∵△ ABE ≌△ CBE ( 已证） ∴ ∠AEB=∠ CEB （全等三角形的对应角相等） ∴ ∠AED=∠ CED （等角的补角相等） ∵ DF AE,DG CE, ∴ ∠AEB=∠ CEB 在△ DEF 和△ DEG 中 ∴△ GEF ≌△ DEG （ AAS) ∴ DF=DG ( 全等三角形的对应边相等）