2010年海南省中考数学试题 12页

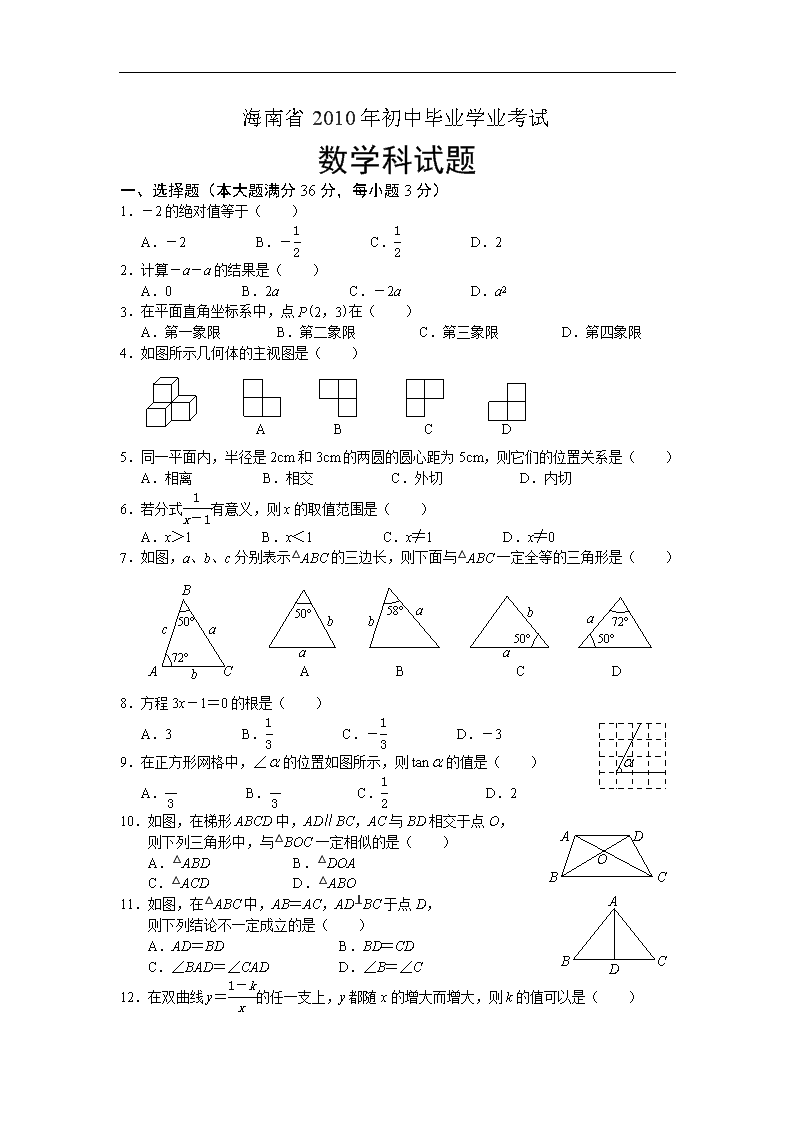
海南省2010年初中毕业学业考试 数学科试题 一、选择题（本大题满分36分，每小题3分）‎ ‎1．－2的绝对值等于（ ）‎ A．－2 B．－ C． D．2‎ ‎2．计算－a－a的结果是（ ）‎ A．0 B．‎2a C．－‎2a D．a2‎ ‎3．在平面直角坐标系中，点P(2，3)在（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．如图所示几何体的主视图是（ ）‎ A B C D ‎5．同一平面内，半径是‎2cm和‎3cm的两圆的圆心距为‎5cm，则它们的位置关系是（ ）‎ A．相离 B．相交 C．外切 D．内切 ‎6．若分式有意义，则x的取值范围是（ ）‎ A．x＞1 B．x＜‎1 C．x≠1 D．x≠0‎ ‎7．如图，a、b、c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（ ）‎ A C B a c b ‎72°‎ ‎50°‎ a a a a b b b ‎50°‎ ‎50°‎ ‎50°‎ ‎58°‎ ‎72°‎ A B C D ‎8．方程3x－1＝0的根是（ ）‎ A．3 B． C．－ D．－3‎ ‎9．在正方形网格中，∠的位置如图所示，则tan的值是（ ）‎ A． B． C． D．2‎ A B C D O ‎10．如图，在梯形ABCD中，AD∥BC，AC与BD相交于点O，‎ 则下列三角形中，与△BOC一定相似的是（ ）‎ A．△ABD B．△DOA A B D C C．△ACD D．△ABO ‎11．如图，在△ABC中，AB＝AC，AD⊥BC于点D，‎ 则下列结论不一定成立的是（ ）‎ A．AD＝BD B．BD＝CD C．∠BAD＝∠CAD D．∠B＝∠C ‎12．在双曲线y＝的任一支上，y都随x的增大而增大，则k的值可以是（ ）‎ A．－1 B．‎0 C．1 D．2‎ 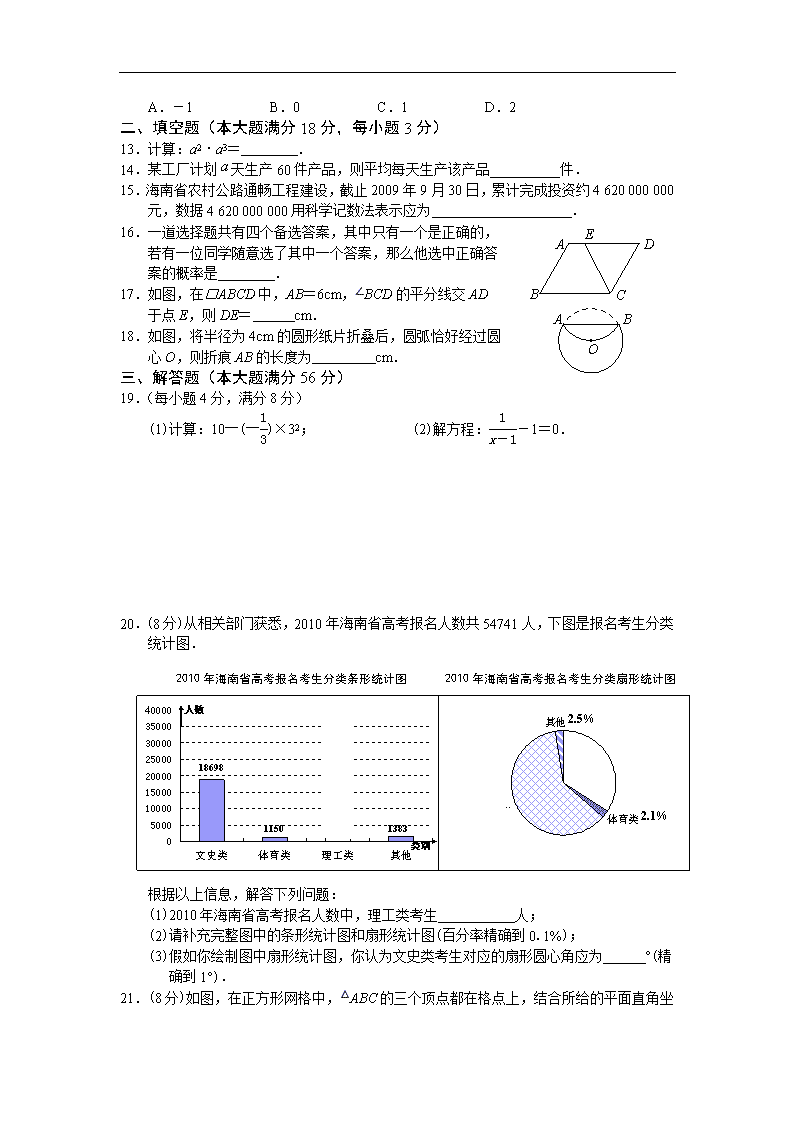二、填空题（本大题满分18分，每小题3分）‎ ‎13．计算：a2·a3＝ ．‎ ‎14．某工厂计划天生产60件产品，则平均每天生产该产品__________件．‎ A B C E D ‎15．海南省农村公路通畅工程建设，截止‎2009年9月30日，累计完成投资约4 620 000 000元，数据4 620 000 000用科学记数法表示应为 ．‎ ‎16．一道选择题共有四个备选答案，其中只有一个是正确的，‎ 若有一位同学随意选了其中一个答案，那么他选中正确答 案的概率是 ．‎ A O B ‎17．如图，在□ABCD中，AB＝‎6cm，∠BCD的平分线交AD 于点E，则DE＝ cm．‎ ‎18．如图，将半径为‎4cm的圆形纸片折叠后，圆弧恰好经过圆 心O，则折痕AB的长度为 cm．‎ 三、解答题（本大题满分56分）‎ ‎19．（每小题4分，满分8分）‎ ‎(1)计算：10―(―)×32； (2)解方程：－1＝0．‎ ‎20．(8分)从相关部门获悉，2010年海南省高考报名人数共54741人，下图是报名考生分类统计图．‎ ‎2.5%‎ ‎5‎ ‎5%‎ ‎18698‎ ‎1383‎ ‎1150‎ 类别 ‎2010年海南省高考报名考生分类条形统计图 人数 ‎2010年海南省高考报名考生分类扇形统计图 ‎2.1%‎ ‎5‎ ‎5%‎ 根据以上信息，解答下列问题：‎ ‎(1)2010年海南省高考报名人数中，理工类考生___________人；‎ ‎(2)请补充完整图中的条形统计图和扇形统计图(百分率精确到0.1%)；‎ ‎(3)假如你绘制图中扇形统计图，你认为文史类考生对应的扇形圆心角应为 °(精确到1°)．‎ ‎21．(8分)如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：‎ ‎(1)将△ABC向右平移5个单位长度，画出平移后的△A1B‎1C1；‎ y C A B O ‎(2)画出△ABC关于x轴对称的△A2B‎2C2；‎ ‎(3)将△ABC绕原点O旋转180°，画出旋转后的△A3B‎3C3；‎ ‎(4)在△A1B‎1C1、△A2B‎2C2、△A3B‎3C3中，‎ ‎△________与△________成轴对称；‎ ‎△________与△________成中心对称．‎ ‎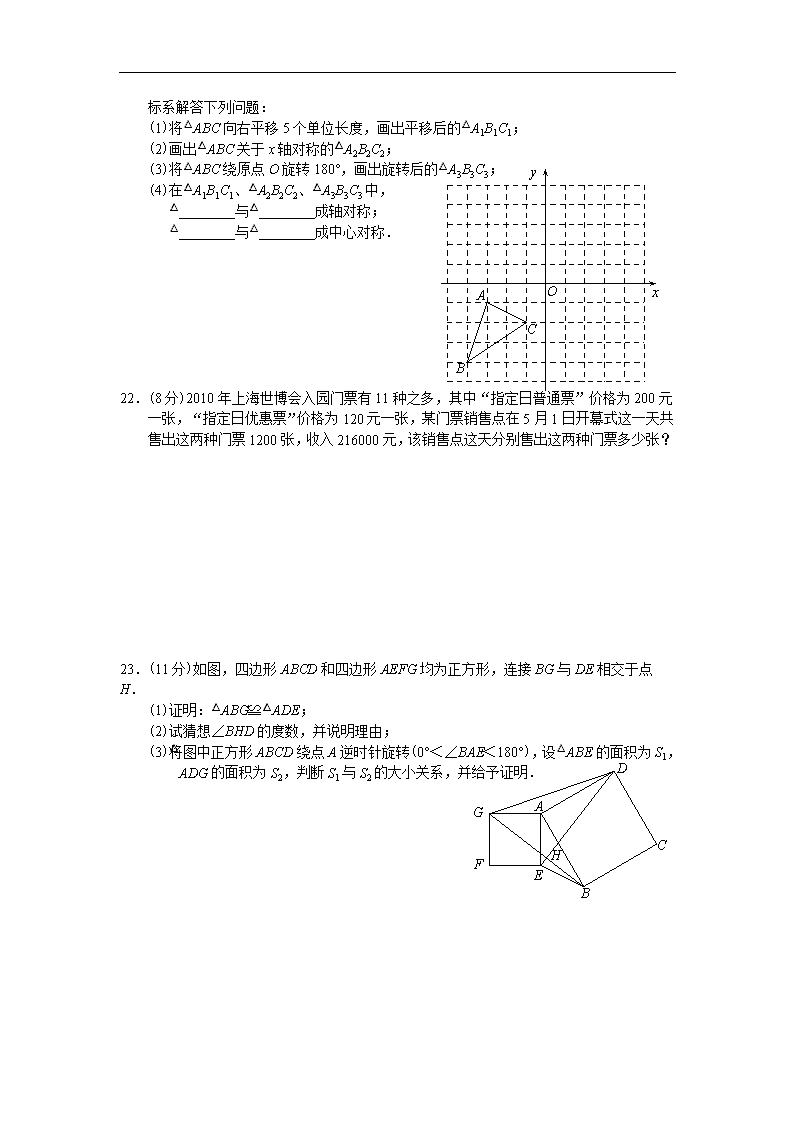22．(8分)2010年上海世博会入园门票有11种之多，其中“指定日普通票”价格为200元一张，“指定日优惠票”价格为120元一张，某门票销售点在‎5月1日开幕式这一天共售出这两种门票1200张，收入216000元，该销售点这天分别售出这两种门票多少张？‎ ‎23．(11分)如图，四边形ABCD和四边形AEFG均为正方形，连接BG与DE相交于点H．‎ ‎(1)证明：△ABG≌△ADE；‎ ‎(2)试猜想∠BHD的度数，并说明理由；‎ A E B C D F G H ‎(3)将图中正方形ABCD绕点A逆时针旋转(0°＜∠BAE＜180°)，设△ABE的面积为S1，△ADG的面积为S2，判断S1与S2的大小关系，并给予证明．‎ ‎24．(13分)如图，在平面直角坐标系中，直线y＝－x＋3与x轴、y轴分别交于点B、C；抛物线y＝－x2＋bx＋c经过B、C两点，并与x轴交于另一点A．‎ ‎(1)求该抛物线所对应的函数关系式；‎ ‎(2)设P(x，y)是(1)所得抛物线上的一个动点，过点P作直线l⊥x轴于点M，交直线BC于点N．‎ A O M B N C P x y l ‎①若点P在第一象限内．试问：线段PN的长度是否存在最大值？若存在，求出它的最大值及此时x的值；若不存在，请说明理由；‎ ‎②求以BC为底边的等腰△BPC的面积．‎ 海南省2010年初中毕业生学业考试数学课时题参考答案 一、选择题(每小题3分，共36分)‎ ‎1． Ｄ　２．Ｃ　３．Ａ　 ４．Ａ　５．Ｃ　６．Ｃ ‎７．Ｂ　８．Ｂ　９．Ｄ　１0．Ｂ　11．Ａ　12．Ｄ 二、填空题(每小题3分，共18分)‎ ‎13、 　 14、　 15、　 ‎ ‎16、　 17、６　 18、‎ 三、解答题(共56分)‎ ‎19．(1)原式＝10-(- )×9 ……1分 ‎ ＝10-(-3) ……2分 ‎ ＝10+3 ……3分 ‎ ＝13 ……4分 ‎ (2)两边都乘以得：‎ ‎ 1-＝0 ……1分 ‎1-＝0 ……2分 ‎＝2 ……3分 检验：当＝2时入≠0，‎ 所以原方程的根是＝2． ……4分 ‎18698‎ ‎1383‎ ‎1150‎ ‎2010年海南省高考报名考生分类条形统计图 人数 ‎33510‎ 类别 ‎2010年海南省高考报名考生分类扇形统计图 ‎61.2%‎ ‎2.5%‎ ‎5‎ ‎5%‎ ‎34.2%‎ ‎2.1%‎ ‎5‎ ‎5%‎ ‎20．‎ 解： (1) 33510 ……3分 ‎(2)如图所示 ……7分 ‎(3) 123 ……8分 B A C A1‎ B1‎ C1‎ A2‎ C2‎ B2‎ B3‎ A3‎ C3‎ y ‎21．(1)△如图所示 ‎ ‎ ……2分 ‎(2)△如图所示 ‎ ‎ ……4分 ‎(3)△如图所示 ‎ ‎……6分 ‎(4)△、△； ‎ ‎△、△‎ ‎……8分 ‎22．解法一：‎ 设该销售点这天售出“指定日普通票张” ，“指定日优惠票”y张，依题意得 ……1分 ‎ ……5分 解得 ……7分 答：这天售出“指定日普通票900张” ，“指定日优惠票”300张．‎ ‎ ……8分 解法二：设该销售点这天售出“指定日普通票张”，则“指定日优惠票”销售了(1200-)张，依题意得 ……1分 ‎200+120(1200-)＝216000 ……5分 ‎ 解得＝900 ∴1200-＝300 ……7分 ‎ 答：这天售出“指定日普通票”900张 ，“指定日优惠票”300张 ． ‎ ‎……8分 ‎23．(1)证法一：‎ 证明：在正方形ABCD和正方形AEFG中 ‎∠GAE＝∠BAD＝90° ……1分 ‎∠GAE+∠EAB＝∠BAD+EAB ‎ 即∠GAB＝∠EAD ……2分 ‎ 又AG＝AE AB＝AD ‎ ‎ ∴△ABG≌△ADE ……4分 证法二：‎ 证明：因为四边形ABCD与四边形AEFG都是正方形，所以∠GAE＝∠BAD＝90°，AG＝AE，AB＝AD，所以△EAD可以看成是△GAB逆时针旋转90°得到，‎ 所以△ABG≌△ADE ‎(2)证法一：‎ 我猜想∠BHD＝90°理由如下：‎ ‎∵△ABG≌△ADE ∴∠1＝∠2 ……5分 而∠3＝∠4 ∴∠1+∠3＝∠2+∠4‎ ‎∵∠2+∠4＝90 ∠1+∠3＝90° ……6分 ‎∴∠BHD＝90° ……7分 证法二：‎ 我猜想∠BHD＝90°理由如下：‎ 由(1)证法(二)可知△EAD可以看成是△GAB逆时针旋转90°得到，BG与DE是一组对应边，‎ 所以BG⊥DE，即∠BHD＝90°‎ ‎(3)证法一：‎ 当正方形ABCD绕点A逆时针旋转 ‎0°＜∠BAE＜180°时,S1和S2总保持相等． ……8分 证明如下：由于0°＜∠BAE＜180°因此分三种情况：‎ ‎①当0°＜∠BAE＜90°时 (如图10)‎ 过点B作BM⊥直线AE于点M，‎ 过点D作DN⊥直线AG于点N．‎ C A B D E G F M N 图10‎ Ｈ ‎1‎ ‎3‎ ‎2‎ ‎4‎ ‎∵∠MAN＝∠BAD＝90°‎ ‎∴∠MAB＝∠NAD 又∠AMB＝∠AND＝90° AB＝AD ‎∴△AMB≌△AND ‎ ‎∴BM＝DN 又AE＝AG ‎∴‎ ‎∴ ……９分 ‎②当∠BAE＝90°时 如图10()‎ ‎∵AE＝AG ∠BAE ＝∠DAG ＝90°AB＝AD ‎∴△ABE≌△ADG A B C D E F G 图10（b）‎ Ae B C D E F G 图10（）‎ ‎∴ 　　　　 ……１０分 ‎③当90°＜∠BAE＜180°时 如图10(b)‎ 和①一样；同理可证 综上所述，在(3)的条件下，总有．‎ ‎ ……11分 证法二：‎ ‎①当0°＜∠BAE＜90°时，如图10(c)‎ A B D E G F 图10(c)‎ Ｈ M N C 作EM⊥AB于点M，作GN⊥AD 交DA延长线于点N，‎ 则∠GNA＝∠EMA＝90°‎ 又∵四边形ABCD与 四边形AEFG都是正方形，‎ ‎∴AG＝AE，AB＝AD ‎∴∠GAN+∠EAN＝90°，‎ ‎∠EAM+∠EAN＝90°‎ ‎∴∠GAN＝∠EAM ‎∴△GAN≌△EAM(AAS)∴GN＝EM ‎∵‎ ‎ ∴‎ ‎②③同证法一类似 证法三：‎ 当正方形ABCD绕点A逆时针旋转 ‎0°＜∠BAE＜180°时,S1和S2总保持相等． ……8分 ‎ 证明如下：由于0°＜∠BAE＜180°因此分三种情况：‎ ‎①当0°＜∠BAE＜90°时　如图10(d)‎ 延长GA至M使AM＝AG，连接DM，则有 Ａ Ｂ Ｃ Ｄ Ｅ Ｆ Ｇ H Ｍ 图10（d）‎ ‎1‎ ‎2‎ ‎3‎ ‎∵AE＝AG＝AM，AB＝AD 又∠1+∠2＝90°‎ ‎∠3+∠2＝90°‎ ‎∴∠1＝∠3‎ ‎∴△ABE≌△ADM (SAS)‎ ‎∴‎ ‎∴　　　　　　　　　　　　　……９分 ‎②当∠BAE＝90°时 (同证法一)　……10分 A B C D E F G 图10（e）‎ M ‎③当90°＜∠BAE＜180°时 ‎ 如图10(e)‎ 和①一样；‎ 同理可证 综上所述，在(3)的条件下，‎ 总有 ‎……11分 证法四：‎ ‎①当0°＜∠BAE＜90°时如图10(f)‎ C B M Ｈ A D G F 图10(f)‎ E 延长DA至M使AM＝AD，连接GM，‎ 则有 再通过证明 ‎△ABE与△AMG全等 从而证出 　‎ ‎②③同证法一类似 证法五：‎ ‎(这种证法用三角函数知识证明，无须分类证明)‎ 如图10(g)‎ 四边形ABCD与四边形AEFG都是正方形，‎ ‎∴AG＝AE，AB＝AD 当∠BAE＝时，∠GAD＝180°-则 sin(180°-)＝sin C A B E G F 图10(g)‎ Ｈ D ‎ 即 ‎∴‎ ‎24．(1)由于直线经过B、C两点,‎ 令y＝0得＝3；令＝0，得y＝3‎ ‎∴B(3，0)，C(0，3) ……1分 ‎∵点B、C在抛物线上，于是得 ‎ ……2分 ‎ 解得b＝2，c＝3 ……3分 ‎∴所求函数关系式为 ……4分 ‎(2)①∵点P(,y)在抛物线上，‎ 且PN⊥x轴，‎ ‎∴设点P的坐标为(, ) ……5分 同理可设点N的坐标为(，) ……6分 又点P在第一象限， ‎ ‎∴PN＝PM-NM B A C P O l N M ‎＝()-()‎ ‎＝‎ ‎＝ ‎ ‎ ……7分 ‎∴当时，‎ 线段PN的长度的最大值为． ……8分 ‎②解法一：‎ 由题意知，点P在线段BC的垂直平分线上，‎ 又由①知，OB＝OC ‎∴BC的中垂线同时也是∠BOC的平分线，‎ ‎∴设点P的坐标为 又点P在抛物线上,于是有 ∴ ……9分 解得 ……10分 ‎∴点P的坐标为：‎ ‎ 或 …11分 若点P的坐标为 ，此时点P在第一象限，在Rt△OMP和Rt△BOC中， ，OB＝OC＝3‎ ‎ ‎ O N l M P C A B P ‎ ‎ ‎ ‎ ‎ ‎ ‎……12分 ‎ ‎ 若点P的坐标为 ， 此时点P在第三象限， ‎ 则 ‎ ……13分 解法二：由题意知，点P在线段BC的垂直平分线上，‎ 又由①知，OB＝OC ‎∴BC的中垂线同时也是∠BOC的平分线，‎ ‎∴设点P的坐标为 又点P在抛物线上，于是有 ∴ ……9分 解得 ……10分 ‎∴点P的坐标为:‎ ‎ 或 …11分 若点P的坐标为 ，此时点P在第一象限，在Rt△OMP和Rt△BOC中，‎ ‎ ，OB＝OC＝3‎ ‎＝‎ ‎＝‎ ‎＝‎ ‎……12分 ‎＝‎ 若点P的坐标为 ， 此时点P在第三象限，(与解法一相同) ……13分 当点P在第一象限时，△BPC面积其它解法有：‎ ‎①，BC＝‎ ‎②‎ ‎ ‎ ‎ ‎ ‎ ‎