苏州市2016年中考数学卷 12页

‎2016年苏州市初中毕业暨升学考试试卷 数 学 注意事项：‎ ‎1．本试卷共21题，满分130分，考试用时150分钟；‎ ‎2．答题前，考生务必将由己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡的相应位置上，井认真核对条形码上的准考号、姓名是否与本人的相符合；‎ ‎3．答选择题须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净 ‎ 后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；‎ ‎4.考生答题,必须答在答题卡上，答在试卷和草稿纸上无效。‎ 一、选择题：本大题目共10小题．每小题3分．共30分．在每小题给出的四个选项中，只有一顶是 ‎ 符合题目要求的．请将选择题的答案用2B铅笔涂在答题卡相应位置上．‎ ‎1. 的倒数是 A. B. C. D. ‎ ‎2.肥皂泡的泡壁厚度大约是0.0007㎜，将0.0007用科学记数法科表示为（）‎ A. B. C. D. ‎ ‎3.下列运算结果正确的是 A. B. ‎ C. D. ‎ ‎4.一次数学测试后，某班40名学生的成绩被分为5组，第14组的频数分别为12、10、6、8，则第5组的频数是 A.0.1 B.0.2 C.0.3 D.0.4‎ ‎5.如图，直线,直线与、分别相交于A、B两点，过点A做直线的垂线交直线于点C，若∠1=58°，则 ‎∠2的度数为 A.58° B.42° C.32° D.28°‎ ‎6.已知点、都是反比例函数的图像上，则、的大小关系为 A. B. C. D.无法比较 ‎7.根据国家发改委实施“阶梯水价”的有关文件要求，某市结合地方实际，决定从20161月1日起对居民生活用水按照新的“阶梯水价”标准收费，某中学研究性学习小组的同学们在社会实践活动中调查了50户家庭某月的用水量，如小表所示：‎ 用水量（吨）‎ ‎15‎ ‎20‎ ‎25‎ ‎30‎ ‎35‎ 户数 ‎3‎ ‎6‎ ‎7‎ ‎9‎ ‎5‎ 则这30户家庭该月应水量的众数和中位数分别是 A.25 ，27.5 B.25，25 C.30 ，27.5 D. 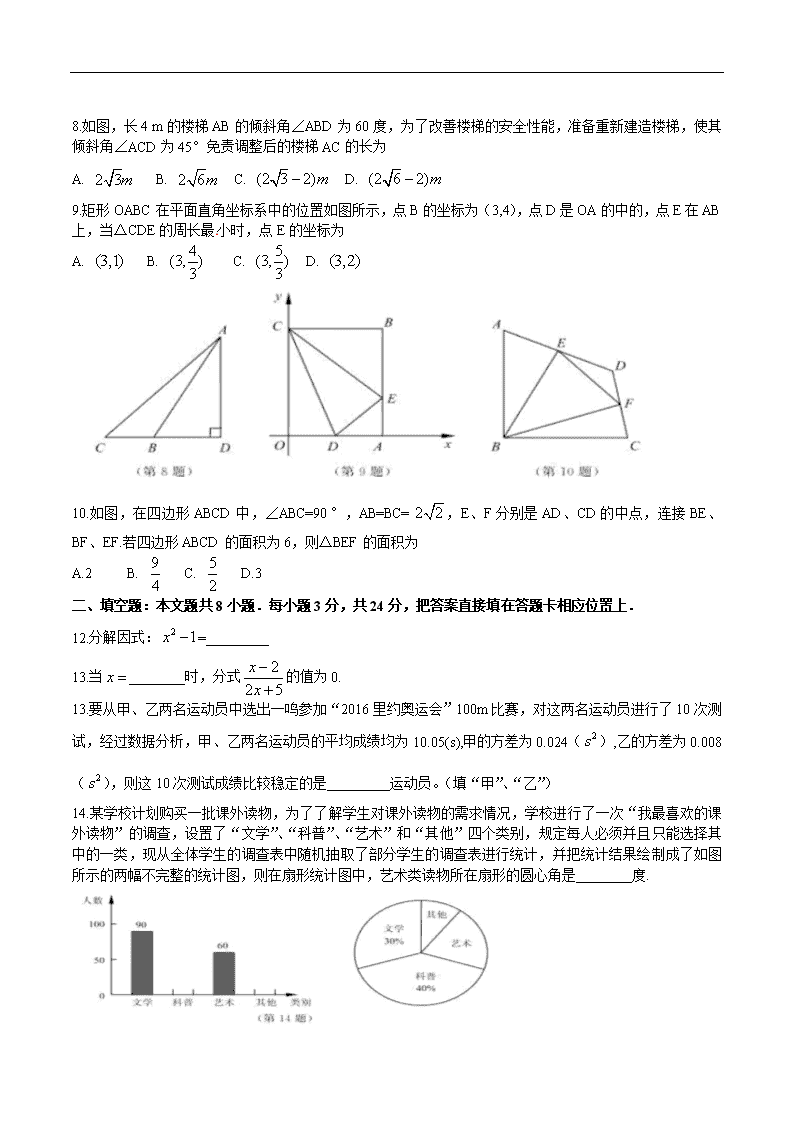30 ，25‎ ‎8.如图，长4 m的楼梯AB的倾斜角∠ABD为60度，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°免责调整后的楼梯AC的长为 A. B. C. D. ‎ ‎9.矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3,4），点D是OA的中的，点E在AB上，当△CDE的周长最小时，点E的坐标为 A. B. C. D. ‎ ‎10.如图，在四边形ABCD中，∠ABC=90°，AB=BC=，E、F分别是AD、CD的中点，连接BE、BF、EF.若四边形ABCD的面积为6，则△BEF的面积为 A.2 B. C. D.3‎ 二、填空题：本文题共8小题．每小题3分，共24分，把答案直接填在答题卡相应位置上．‎ ‎12.分解因式：=_________‎ ‎13.当________时，分式的值为0.‎ ‎13.要从甲、乙两名运动员中选出一鸣参加“2016里约奥运会”100m比赛，对这两名运动员进行了10次测试，经过数据分析，甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024（）,乙的方差为0.008（），则这10次测试成绩比较稳定的是_________运动员。（填“甲”、“乙”）‎ ‎14.某学校计划购买一批课外读物，为了了解学生对课外读物的需求情况，学校进行了一次“我最喜欢的课外读物”的调查，设置了“文学”、“科普”、“艺术”和“其他”四个类别，规定每人必须并且只能选择其中的一类，现从全体学生的调查表中随机抽取了部分学生的调查表进行统计，并把统计结果绘制成了如图所示的两幅不完整的统计图，则在扇形统计图中，艺术类读物所在扇形的圆心角是________度.‎ ‎15.不等式组的最大整数解是_________.‎ ‎16.如图，AB是圆O的直径，AC是圆O的弦，过点C的切线交AB的延长线于点D，若 ‎∠A=∠D，CD=3，则图中阴影部分的面积为________‎ ‎17.如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到（点在四边形ADEC内），连接，则的长为________‎ ‎18.如图，在平面直角坐标系中，已知点A、B的坐标分别、，C是AB的中点，过C作轴的垂线垂足为D.动点P从点D出发，沿DC向C匀速运动，过点P做轴的垂线，垂足为E，连接BP、EC.当BP所在直线与EC所在直线第一次垂直时，点P的坐标为_________.‎ 三、解答题：本大题共10小题．共76分，把解答过程写在答题卡相应位置上．解答时应写出必要的计算过程，推演步骤或文字说明．作答时用2B铅笔或黑色墨水签字笔.‎ ‎19.（本题满分5分）‎ 计算：‎ ‎20.（本题满分5分）‎ 解不等式，并把它的解集在数轴上表示出来.‎ ‎21. （本题满分6分）‎ 先化简，在求值：，其中.‎ ‎22. （本题满分6分）某停车场的收费标准如下：中型汽车的停车费为12元/辆，小型汽车的停车费为8元/辆，现在停车场共有50辆中、小汽车，这些车共缴纳停车费480元，中、小型汽车各有多少辆？‎ ‎23. （本题满分8分）在一个不透明的布袋中装有三个小球，小球上分别标有数字、0、2，它们除了数字不同外，其他都完全相同．‎ ‎(1)随机地从布袋中摸出一个小球，则摸出的球为标有数字2的小球的概率为______； ‎ ‎(2)小丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的横坐标，‎ ‎ 再将此球放回、搅匀，然后由小华再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的纵坐．请用树状图或表格列出点M所有可能的坐标，并求出点M落在如图所示的正方形网格内（包括边界）的概率.‎ ‎24. （本题满分8分）如图，在菱形ABCD中，对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E．‎ ‎(1)证明：四边形ACDE是平行四边形；‎ ‎(2)若AC=8，BD=6，求△ADE的周长．‎ ‎25. （本题满分8分）如图一次函数的图像与轴交千点A，与反比例函数的图像交干点B (2,n)．过点B作轴于点P，是该反比例函数图像上的一点，且∠PBC=∠ABC．求反比例函数和一次函数的表达式．‎ ‎26. （本题满分10分）如图，AB是圆O的直径，D、E为圆O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD．连接AC交圆O于点F，连接AE、DE、DF.‎ ‎（1）证明：∠E=∠C，‎ ‎（2）若∠E=55°，求∠BDF的度数，‎ ‎（3）设DE交AB于点G，若DF=4， ，E是弧AB的中点，求的值．‎ ‎27. （本题满分10分）如图，在矩形ABCD中，AB =6cm，AD =8 cm.点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作圆O，点P与点O同时出发，设它们的运动时间为 (单位：s）‎ ‎ （1）如图1，连接DQ，当DQ平分∠BDC时，t的值为_______‎ ‎ (2)如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；‎ ‎ （3）请你继续连行探究，并解答下列问题：‎ ‎ ①证明：在运动过程中，点O始终在QM所在直线的左侧；‎ ‎ ②如图3，在运动过程中，当QM与圆O相切时，求t的值；并判断此时PM与圆O是 ‎ 否也相切？说明理由．‎ ‎28. （本题满分10分）如图，直线与轴、轴分别相交于A、B两点，抛物线经过点B．‎ ‎ (1)求该地物线的函数表达式；‎ ‎ (2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM．设点M的横坐标为，△ABM的面积为S．求S与的函数表达式，并求出S的最大值；‎ ‎ (3)在(2)的条件下，当S取得最大值时，动点M相应的位置记为点.‎ ‎ ①写出点的坐标；‎ ‎ ②将直线绕点A按顺时针方向旋转得到直线，当直线与直线重合时停止旋转．在旋转过程中，直线与线段交于点C．设点B、到直线的距离分别为 ‎、，当最大时，求直线旋转的角度（即∠BAC的度数）．‎