全国名校中考数学模拟试卷分类汇编 31 解直角三角形的应用 7页

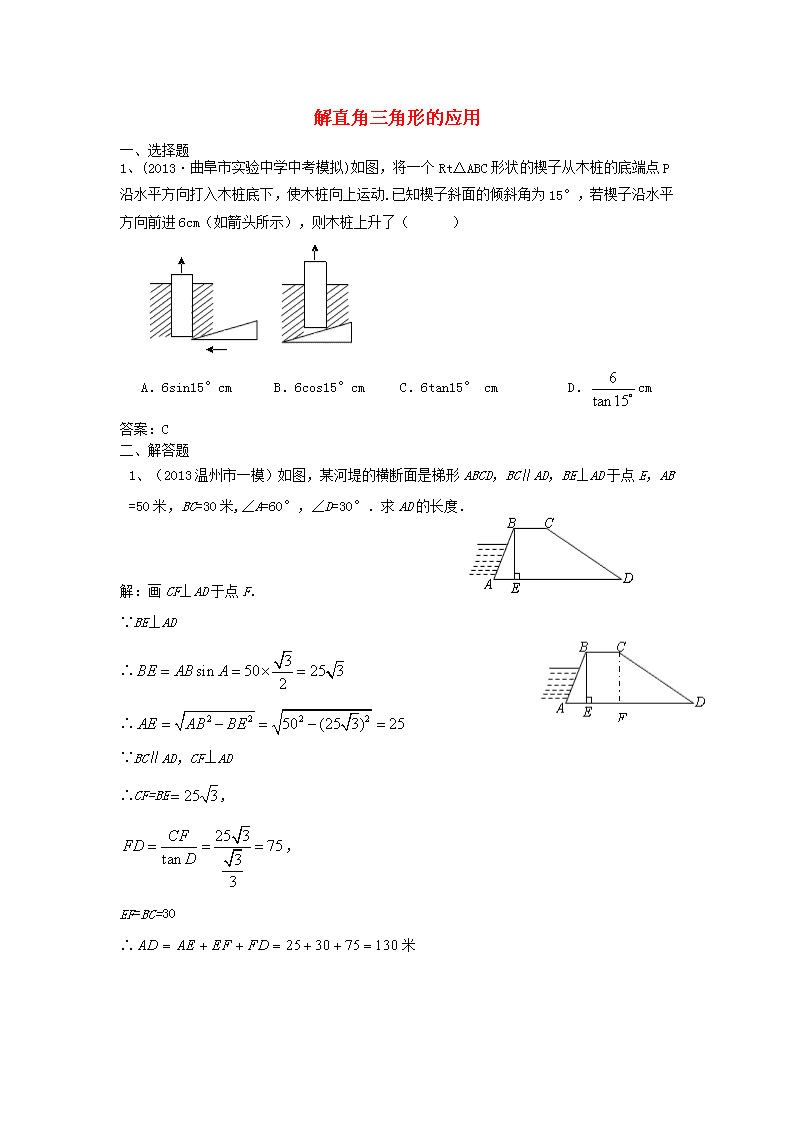
解直角三角形的应用 一、选择题 ‎1、(2013·曲阜市实验中学中考模拟)如图，将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下，使木桩向上运动.已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm（如箭头所示），则木桩上升了（ ）‎ A．6sin15°cm B．6cos15°cm C．6tan15° cm D．cm ‎ 答案：C 二、解答题 ‎1、（2013温州市一模）如图，某河堤的横断面是梯形ABCD，BC∥AD，BE⊥AD于点E，AB =50米，BC=30米,∠A=60°，∠D=30°．求AD的长度．‎ 解：画CF⊥AD于点F．‎ ‎∵BE⊥AD F ‎∴ ‎ ‎∴‎ ‎∵BC∥AD，CF⊥AD ‎∴CF=BE, ‎ ‎，‎ EF=BC=30 ‎ ‎∴米 ‎ ‎2、(2013·吉林中考模拟)已知，如图，在坡顶A处的同一水平面上有一座古塔BC，数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1∶2.4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°．‎ 求：（1）坡顶A到地面PQ的距离；‎ ‎（2）古塔BC的高度（结果精确到1米）．‎ ‎（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）‎ 答案：解：（1）过点A作AH⊥PQ，垂足为点H．‎ ‎∵斜坡AP的坡度为1∶2.4，∴． …………… 2分 ‎ 设AH=5k，则PH=12k，由勾股定理，得AP=13k．‎ ‎∴13k=26．解得k=2．∴AH=10． ‎ 答：坡顶A到地面PQ的距离为10米． …………… 4分 ‎ ‎（2）延长BC交PQ于点D．‎ ‎∵BC⊥AC，AC∥PQ，∴BD⊥PQ． ‎ ‎∴四边形AHDC是矩形，CD=AH=10，AC=DH． ‎ ‎∵∠BPD=45°，∴PD=BD． ‎ 设BC=x，则x+10=24+DH．∴AC=DH=x－14．‎ 在Rt△ABC中，，即． ………6分 ‎ 解得，即． ………… 7分 ‎ 答：古塔BC的高度约为19米． ………… 8分 ‎ ‎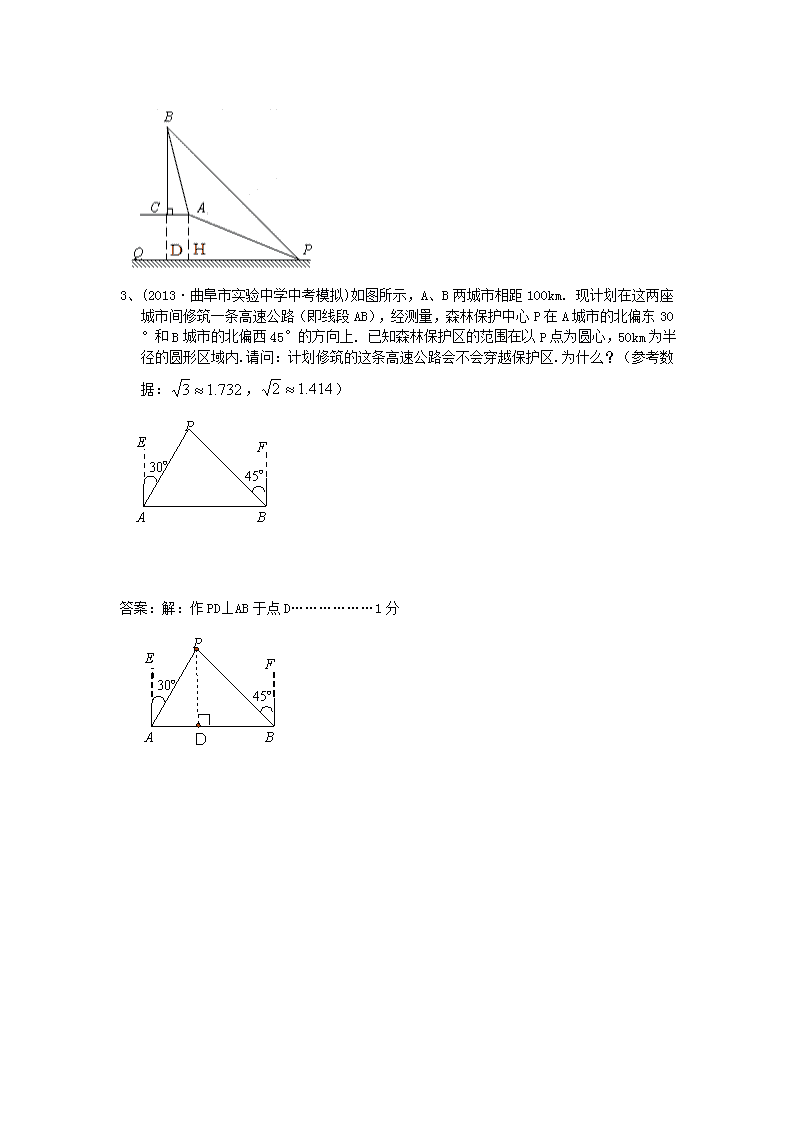3、(2013·曲阜市实验中学中考模拟)如图所示，A、B两城市相距100km. 现计划在这两座城市间修筑一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上. 已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内. 请问：计划修筑的这条高速公路会不会穿越保护区. 为什么？（参考数据：，）‎ P A B E F ‎30º ‎45º 答案：解：作PD⊥AB于点D………………1分 ‎4、（2013·温州市中考模拟）如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为12m．求旗杆的高度．‎ ‎ ‎ ‎ ‎ 答案：解：过点A作AE⊥BC，垂足为E，得矩形ADCE，∴CE=AD=12. ‎ ‎ PC=PA·cos∠APC=30…………………………………2分 ‎ 在Rt△PCB中，………………………1分 …………………………………2分 答：当渔船位于P南偏东45°方向时，渔船与P的距离是30海里。……1分 ‎6、(2013年河北省一摸)|如图11是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°． 已知原传送带AB长为‎4‎米．‎ ‎（1）求新传送带AC的长度；‎ ‎（2）如果需要在货物着地点C的左侧留出‎2米的通道，试判断距离B点‎5米的货物MNQP是否需要挪走，并说明理由．（≈1.4，≈1.7）‎ 答案：（1）在Rt△ABD中，AD=ABsin45°=，……………………………2分 ‎ ∴在Rt△ACD中，AC==2AD=8，‎ 即新传送带AC的长度约为‎8米．……………………………………………4分 ‎（2）结论：货物MNQP不需挪走． ……………………………………………5分 解：在Rt△ABD中，BD=ABcos45°= ‎ ‎ 在Rt△ACD中，CD=ACcos30°= ∴CB=CD—BD= ‎ ‎∵PC=PB—CB =5—()=9—≈2.2>2 ‎ ‎ ∴货物MNQP不需挪走． ………………………………………………8分 ‎7、(2013年河北三摸)如图，风车的支杆OE垂直于桌面，风车中心O到桌面的距离OE为‎25cm，风车在风吹动下绕着中心O不停地转动，转动过程中，叶片端点A、B、C、D在同一圆O上，已知⊙O的半径为‎10cm.。‎ ‎（1）风车在转动过程中，点为A到桌面的最远距离为_____cm，最近距离为_____cm；‎ ‎（2）风车在转动过程中，当∠AOE＝45°时，求点A到桌面的距离(结果保留根号)．‎ ‎（3）在风车转动一周的过程中，求点A相对于桌面的高度不超过‎20cm所经过的路径长(结果保留π)．‎ 解：（1）35，15；………….2分 ‎（2）点A运动到点A1的位置时∠AOE＝45°. ‎ 作A‎1F⊥MN于点F，A‎1G⊥OE于点G，∴　A‎1F＝GE. ‎ 在Rt△A1OG中，‎ ‎∵∠A1OG＝45°，OA1＝10，‎ ‎∴OG＝OA1·cos45°＝10×＝5.‎ ‎∵OE＝25，∴GE＝OE－OG＝25－5. ∴A‎1F＝GE＝25－5. ‎ 答：点A到桌面的距离是(25－5)厘米………………5分 ‎（3）点A在旋转过程中运动到点A2、A3的位置时，点A到桌面的距离等于‎20厘米. ‎ 作A2H⊥MN于H，则A2H＝20. 作A2D⊥OE于点D，‎ ‎∴DE＝A2H.‎ ‎∵OE＝25，‎ ‎∴OD＝OE－DE＝25－20＝5. ‎ 在Rt△A2OD中，‎ ‎∵OA2＝10，‎ ‎∴cos∠A2OD＝＝＝. ‎ ‎∴∠A2OD＝60°.‎ 由圆的轴对称性可知，∠A3OA2＝2∠A2OD＝120°. ‎ ‎∴点A所经过的路径长为＝.‎ 答：点A所经过的路径长为厘米． . ………………………………………………10分 ‎8、（2013年温州一摸）如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面的高AD为‎12m．求旗杆的高度．‎ ‎ ‎ ‎ ‎ 答案：‎ 解：过点A作AE⊥BC，垂足为E，得矩形ADCE，∴CE=AD=12. ‎ Rt△ACE中，∵∠EAC=60°，CE=12，‎ ‎∴AE=. ‎ Rt△ABE中，∵∠BAE=30°，BE=AE.‎ ‎∴BC=CE+BE=‎16m.‎