2007年中考数学湖南省娄底市试卷 10页

湖南省娄底市2007年初中毕业学业考试数学试卷 考生注意：本学科试卷共六道大题，满分120分，考试时量120分钟．‎ B C A D 一、填空题（本大题共8个小题，每小题3分，满分24分）‎ ‎1．16的平方根是__________．‎ ‎2．如图，在△ABC中，∠ABC＝90º，∠C＝40º，‎ AC∥BD，则∠ABD＝__________．‎ ‎3．根据国务院全面实行农村义务教育经费保障机制改革的精神，据《潇湘晨报》‎2月28日报道：2007年春季开学，我省投入19.8114亿元，对农村义务教育阶段的学生实行“两免一补”．19.8114亿元用科学记数法（保留两个有效数字）表示为___________元．‎ ‎60cm D D ‎4．如右图所示：用一个半径为‎60cm，圆心角为150º的扇形围成一个圆锥，则这个圆锥的底面半径 为___________．‎ ‎5．我国著名的珠穆朗玛峰海拔高达‎8844米，在它周围‎2千米的附近，耸立的几座著名山峰的高度如下表：‎ 山峰名 珠穆 朗玛 洛子峰 卓穷峰 马卡 鲁峰 章子峰 努子峰 普莫 里峰 海拔高度 ‎8844m ‎8516m ‎7589m ‎8463m ‎7543m ‎7855m ‎7145m 则这七座山峰海拔高度的极差为___________米．‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎6．如右图所示，圆盘被分成8个全等的小扇形，分别写上数字 ‎1，2，3，4，5，6，7，8，自由转动圆盘，指针指向的数字小于 ‎3的概率是___________．‎ ‎7．下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第n个图案中白色正方形的个数为___________．‎ 第一个 第二个 第三个 ‎……‎ 第n个 ‎8．如图所示，在四边形ABCD中，AD∥BC，如果要使△ABC∽△DCA，那么还要补充的一个条件是_____________（只要求写出一个条件即可）．‎ A D C B 二、选择题（本大题共8个小题，每小题3分，满分24分．每小题给出四个选项，选出符合题设要求的一项，将其代号填入对应的题号下）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 ‎9．若|a－1|＝1－a，则a的取值范围为（ ）‎ ‎（A）a≥1 （B）a≤1 （C）a＞1 （D）a＜1‎ ‎10．下列各图中，是中心对称图形的是（ ）‎ A．‎ Ｂ．‎ Ｃ．‎ Ｄ．‎ ‎11．下列命题中正确的是（ ）‎ ‎（A）半圆或直径所对的圆周角是直角 ‎（B）相等的角是对顶角 ‎（C）两条直线被第三条直线所截，同位角相等 ‎（D）对角线互相垂直的平行四边形是正方形 ‎12．不等式组的解集是（ ）‎ ‎（A）2＜x≤3 （B）－2＜x＜3‎ A D E C B ‎（C）－2＜x≤3 （D）－2≤x＜3‎ ‎13．如图，将一张等腰直角三角形纸片沿中位线DE剪开后，‎ 可以拼成的四边形是（ ）‎ ‎（A）矩形或等腰梯形 ‎（B）矩形或平行四边形 ‎（C）平行四边形或等腰梯形 ‎（D）矩形或等腰梯形或平行四边形 ‎14．已知△ABC的内切圆⊙O如图，若∠DEF＝54º，则∠BAC等于（ ）‎ ‎（A）96º （B）48º ‎（C）24º （D）72º ‎15．为了吸收国民的银行存款，今年中国人民银行对一年期银行存款利率进行了两次调整，由原来的2.52%提高到3.06%．现李爷爷存入银行a万元钱，一年后，将多得利息（ ）万元．‎ ‎（A）0.44%a （B）0.54%a （C）0.54a （D）0.54%‎ B C G H A E F ‎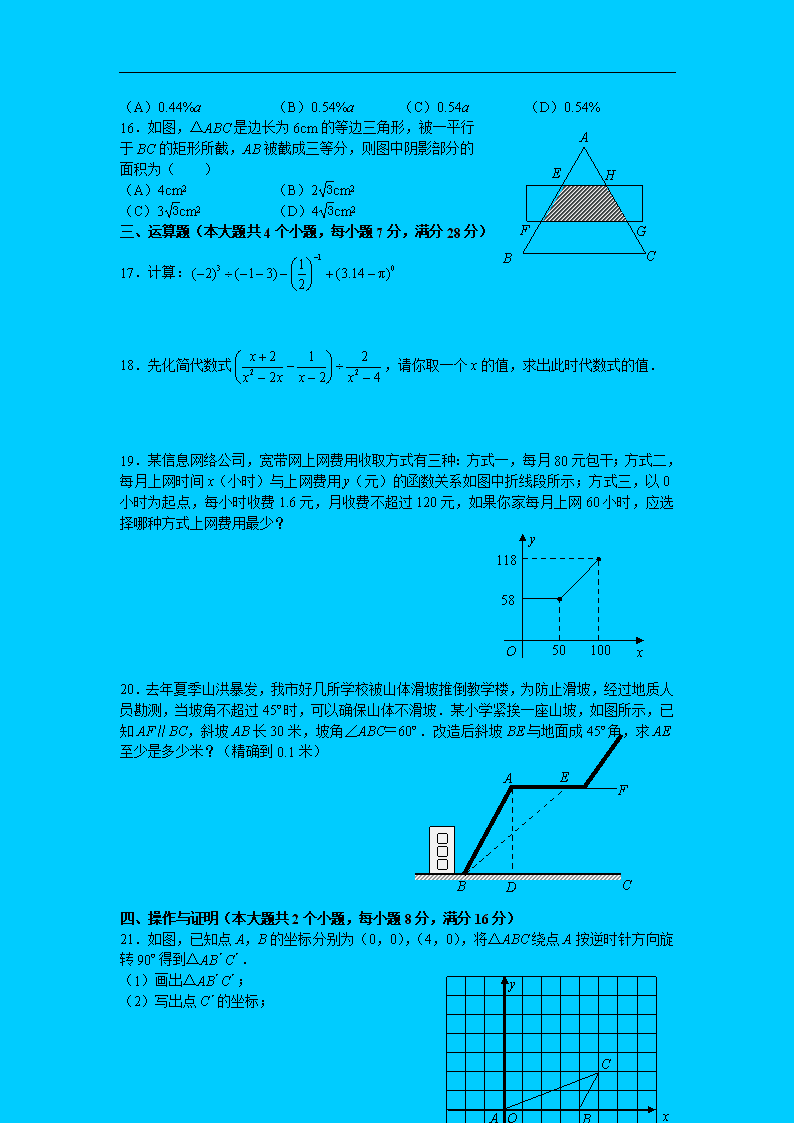16．如图，△ABC是边长为‎6cm的等边三角形，被一平行 于BC的矩形所截，AB被截成三等分，则图中阴影部分的 面积为（ ）‎ ‎（A）4cm2 （B）2cm2 ‎ ‎（C）3cm2 （D）4cm2‎ 三、运算题（本大题共4个小题，每小题7分，满分28分）‎ ‎17．计算：‎ ‎18．先化简代数式，请你取一个x的值，求出此时代数式的值．‎ O ‎50‎ ‎100‎ ‎58‎ ‎118‎ y x ‎19．某信息网络公司，宽带网上网费用收取方式有三种：方式一，每月80元包干；方式二，每月上网时间x（小时）与上网费用y（元）的函数关系如图中折线段所示；方式三，以0小时为起点，每小时收费1.6元，月收费不超过120元，如果你家每月上网60小时，应选择哪种方式上网费用最少？‎ ‎20．去年夏季山洪暴发，我市好几所学校被山体滑坡推倒教学楼，为防止滑坡，经过地质人员勘测，当坡角不超过45º时，可以确保山体不滑坡．某小学紧挨一座山坡，如图所示，已知AF∥BC，斜坡AB长‎30米，坡角∠ABC＝60º．改造后斜坡BE与地面成45º角，求AE至少是多少米？（精确到‎0.1米）‎ B D C F E A 四、操作与证明（本大题共2个小题，每小题8分，满分16分）‎ ‎21．如图，已知点A，B的坐标分别为（0，0），（4，0），将△ABC绕点A按逆时针方向旋转90º得到△AB´C´．‎ B A O C y x ‎（1）画出△AB´C´；‎ ‎（2）写出点C´的坐标；‎ ‎（3）求BB´的长．‎ ‎22．如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．‎ ‎（1）求证：AE＝DF；‎ ‎（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．‎ E A F C D B 五、实验与应用（本大题共2个小题，每小题8分，满分16分）‎ ‎23．某市篮球队到市一中选拔一名队员．教练对王亮和李刚两名同学进行5次3分投篮测试，每人每次投10个球，下图记录的是这两名同学5次投篮中所投中的个数．‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 投中个数 测试序号 王亮 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 投中个数 测试序号 李刚 姓名 平均数 众数 方差 王亮 ‎7‎ 李刚 ‎7‎ ‎2.8‎ ‎（1）请你根据图中的数据，填写右表．‎ ‎（2）你认为谁的成绩比较稳定，为什么？‎ ‎（3）若你是教练，你打算选谁？简要说明理由．‎ ‎24．高速公路有一次抢修任务，竞标资料显示：若由甲、乙两队合作施工，6天可以完成，共需工程费用10200元，若由甲队或乙队单独施工，那么甲队比乙队少用5天施工时间，但甲队每天的工作费用比乙队多300元，问应选哪个队施工经费较少？‎ 六、综合探究（本题满分12分）‎ ‎25．经过x轴上A（－1，0）B（3，0）两点的抛物线y＝ax2＋bx＋c交y轴于点C，设抛物线的顶点为D，若以DB为直径的⊙G经过点C，求解下列问题：‎ ‎（1）用含a的代数式表示出C，D的坐标；‎ ‎（2）求抛物线的解析式；‎ D C O G y x ‎（3）如图，当a＜0时，能否在抛物线上找到一点Q，使△BDQ为直角三角形？你能写出Q点的坐标吗？‎ ‎[参考答案]‎ 一、填空题：本题共8个小题，每小题答对记3分，满分24分．‎ ‎1．　　2．　　3．　　4．‎25cm　　5．1699　　6．　　‎ ‎7．或（的整数）‎ ‎8．或或 二、选择题：本题共8个小题，每小题3分，满分24分．答题选对记3分，选错、多选、不选均记0分．‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 B B A C D D B C 三、运算题（本大题共4个小题，每小题7分，满分28分）‎ ‎17．解：原式 5分 ‎ 6分 ‎ 7分 ‎18．原式 3分 ‎ 5分 ‎（取的值时，注意） 7分 ‎19．解：设用户上网小时，月上网费为元． 1分 按方式一 当时，元．‎ 按方式二 则 ‎ 因直线过和两点 ‎ 解得 ‎ ‎ ‎ 当时，（元）‎ 按方式三 则 且 ‎ 当时，（元） 6分 ‎ 而 ‎ 该选择方式二上网费用少． 7分 ‎20．解：在中，米 ‎ ‎（米） 2分 米 B D C F E A N 连接，过作于 四边形是矩形 米 4分 在中，由已知，‎ 当时 米 6分 米 7分 答：至少是11米．‎ 四、操作与证明（本大题共2个小题，每小题8分，满分16分）‎ ‎21．解：（1）见下图 B A O C y x ‎ 3分 ‎（2）点的坐标为 6分 ‎（3） 8分 ‎22．解：（1），‎ 同理 ‎ 4分 ‎（2）若平分，四边形是菱形．‎ 证明：，‎ 四边形是平行四边形 平行四边形为菱形 8分 五、实践与应用（本大题共2个小题，每小题8分，满分16分）‎ ‎23．解：（1）见下表 姓名 平均数 众数 方差 王亮 ‎7‎ ‎0.4‎ 李刚 ‎7‎ ‎（平均数、众数各1分，方差给2分） （2）两人的平均数、众数相同，从方差上看，王亮投篮成绩的方差小于李刚投篮成绩的方 差．王亮的成绩较稳定． 6分 ‎（3）选王亮的理由是成绩较稳定，选李刚的理由是他具有发展潜力，李刚越到后面投中个数越多．（学生答题时，任选一个，只要理由充分都给2分） 8分 ‎24．解：设甲单独施工需天，则乙单独施工为天 1分 可列出方程 4分 得解之，（不合题意舍去） 5分 设甲队每天费用元，乙队每天费用元 则 解之得 7分 甲队施工经费为（元）‎ 乙队施工经费为（元）‎ 答：应选甲队施工费较少． 8分 六、综合探究（本题满分12分）‎ ‎25．解：（1）设抛物线的解析式为 1分 则 2分 则点的坐标为 3分 D C O G y x E 图①‎ 点的坐标为 4分 ‎（2）过点作轴于，如图①所示：‎ 则有 5分 ‎ 7分 抛物线的解析式为或 8分 D H O G y x E F Q 图②‎ ‎（3）时，，抛物线，‎ 这时可以找到点，很明显，点即在抛物线上，‎ 又在上，，这时与点重合 点坐标为 9分 如图②，若为，作轴于，‎ 轴于 可证 有 则点坐标 即 化简为 即 解之为或 由得坐标： 10分 若为 如图③，延长交轴于，‎ D M O G y x E H 图③‎ 作轴于，‎ 轴于 可证明 即 则 得，点的坐标为 所在的直线方程为 则与的解为，得交点坐标为 11分 即满足题意的点有三个，， 12分