高中数学第一章解三角形1-2-2高度角度问题课时作业含解析新人教A版必修5 8页

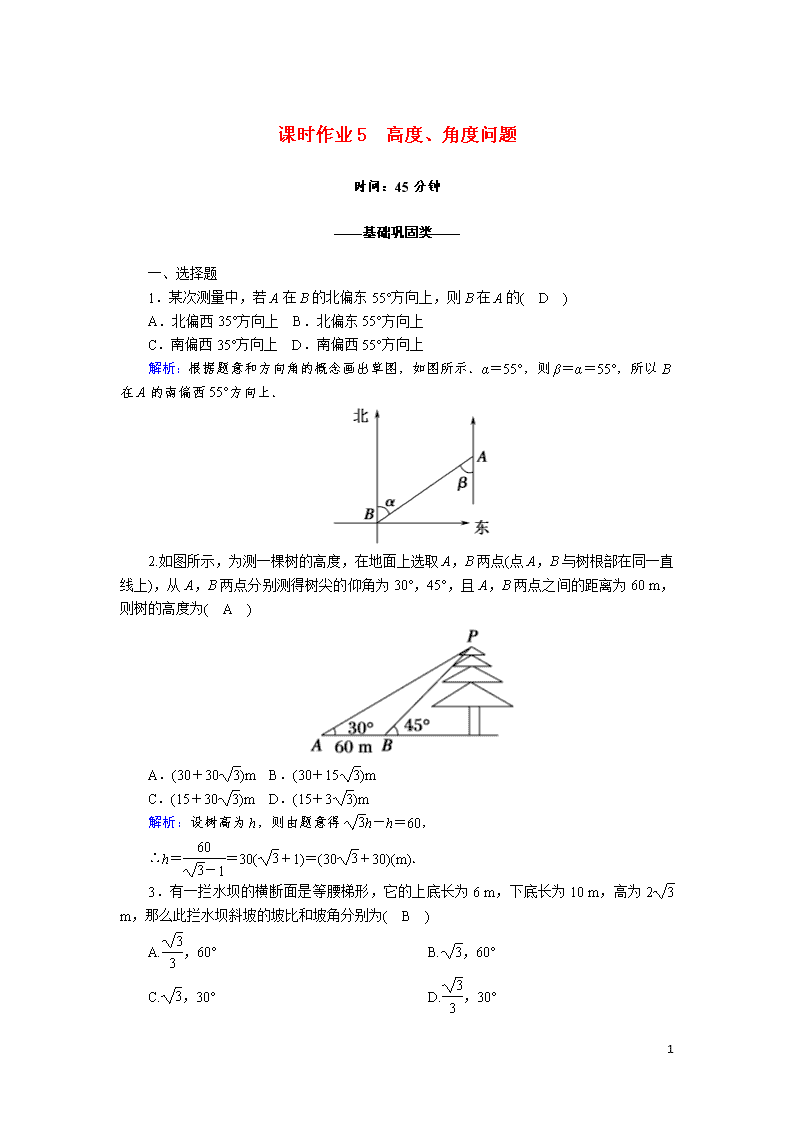
课时作业5　高度、角度问题 时间：45分钟 ‎——基础巩固类——‎ 一、选择题 ‎1．某次测量中，若A在B的北偏东55°方向上，则B在A的(　D　)‎ A．北偏西35°方向上 B．北偏东55°方向上 C．南偏西35°方向上 D．南偏西55°方向上 解析：根据题意和方向角的概念画出草图，如图所示．α＝55°，则β＝α＝55°，所以B在A的南偏西55°方向上．‎ ‎2.如图所示，为测一棵树的高度，在地面上选取A，B两点(点A，B与树根部在同一直线上)，从A，B两点分别测得树尖的仰角为30°，45°，且A，B两点之间的距离为60 m，则树的高度为(　A　)‎ A．(30＋30)m B．(30＋15)m C．(15＋30)m D．(15＋3)m 解析：设树高为h，则由题意得h－h＝60，‎ ‎∴h＝＝30(＋1)＝(30＋30)(m)．‎ ‎3．有一拦水坝的横断面是等腰梯形，它的上底长为6 m，下底长为10 m，高为2 m，那么此拦水坝斜坡的坡比和坡角分别为(　B　)‎ A.，60° B.，60°‎ C.，30° D.，30°‎ 8‎ 解析：如图所示，横断面是等腰梯形ABCD，AB＝10 m，CD＝6 m，高DE＝2 m，则AE＝＝2 m，‎ ‎∴tan∠DAE＝＝＝，∴∠DAE＝60°.‎ ‎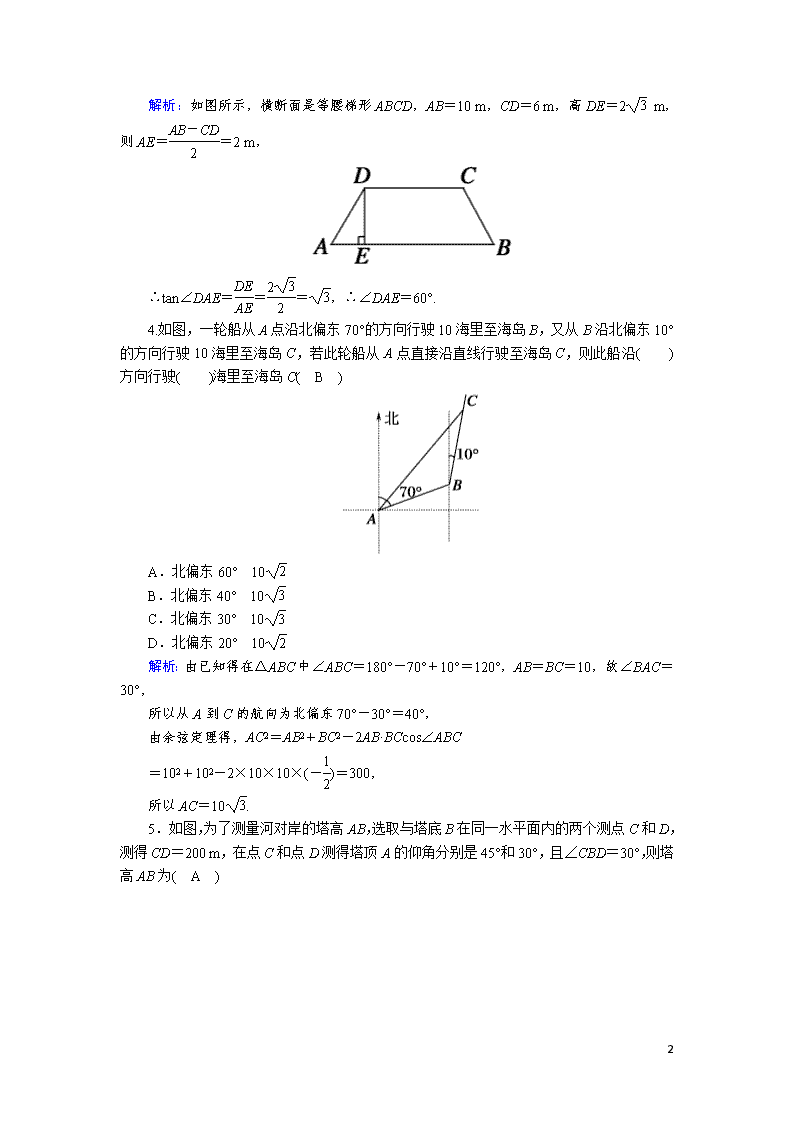4.如图，一轮船从A点沿北偏东70°的方向行驶10海里至海岛B，又从B沿北偏东10°的方向行驶10海里至海岛C，若此轮船从A点直接沿直线行驶至海岛C，则此船沿(　　)方向行驶(　　)海里至海岛C(　B　)‎ A．北偏东60°　10 B．北偏东40°　10 C．北偏东30°　10 D．北偏东20°　10 解析：由已知得在△ABC中∠ABC＝180°－70°＋10°＝120°，AB＝BC＝10，故∠BAC＝30°，‎ 所以从A到C的航向为北偏东70°－30°＝40°，‎ 由余弦定理得，AC2＝AB2＋BC2－2AB·BCcos∠ABC ‎＝102＋102－2×10×10×(－)＝300，‎ 所以AC＝10.‎ ‎5．如图，为了测量河对岸的塔高AB，选取与塔底B在同一水平面内的两个测点C和D，测得CD＝200 m，在点C和点D测得塔顶A的仰角分别是45°和30°，且∠CBD＝30°，则塔高AB为(　A　)‎ 8‎ A．200 m B．100 m C．200 m D．300 m 解析：在Rt△ABC中，∠ACB＝45°，设AB＝h，则BC＝h.在Rt△ABD中，∠ADB＝30°，则BD＝h，在△BCD中，由余弦定理，得CD2＝BC2＋BD2－2·BC·BD·cos∠CBD，即2002＝h2＋(h)2－2·h·h·，解得h＝200(h＝－200舍去)，即塔高AB＝200 m.‎ ‎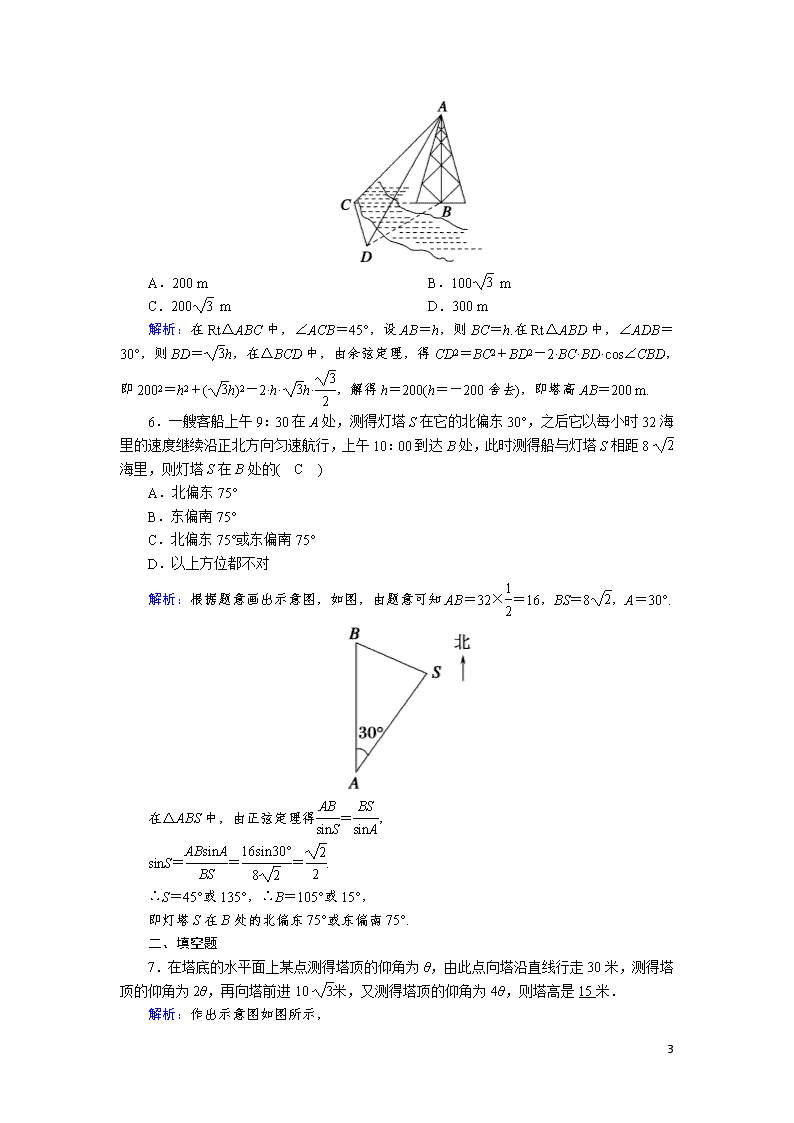6．一艘客船上午9：30在A处，测得灯塔S在它的北偏东30°，之后它以每小时32海里的速度继续沿正北方向匀速航行，上午10：00到达B处，此时测得船与灯塔S相距8海里，则灯塔S在B处的(　C　)‎ A．北偏东75°‎ B．东偏南75°‎ C．北偏东75°或东偏南75°‎ D．以上方位都不对 解析：根据题意画出示意图，如图，由题意可知AB＝32×＝16，BS＝8，A＝30°.‎ 在△ABS中，由正弦定理得＝，‎ sinS＝＝＝.‎ ‎∴S＝45°或135°，∴B＝105°或15°，‎ 即灯塔S在B处的北偏东75°或东偏南75°.‎ 二、填空题 ‎7．在塔底的水平面上某点测得塔顶的仰角为θ，由此点向塔沿直线行走30米，测得塔顶的仰角为2θ，再向塔前进10米，又测得塔顶的仰角为4θ，则塔高是15米．‎ 解析：作出示意图如图所示，‎ 8‎ 由题意知∠ABC＝θ，∠ACD＝2θ，∠ADE＝4θ，‎ AC＝BC＝30米，AD＝CD＝10米．‎ 在△ACD中，cos2θ＝＝＝，‎ 所以sin2θ＝.‎ 在Rt△ACE中，AE＝ACsin2θ＝30×＝15(米)．‎ ‎8．若某人从A处出发，沿北偏东60°方向行走3 km到B处，再沿正东方向行走2 km到C处，则A，C两地之间的距离为7 km.‎ 解析：画出草图，如图所示，由题意可知AB＝3，BC＝2，∠ABC＝150°.在△ABC中，由余弦定理，得AC2＝27＋4－2×3×2×cos150°＝49，所以AC＝7，所以A，C两地之间的距离为7 km.‎ ‎9．一船以24 km/h的速度向正北方向航行，在点A处望见灯塔S在船的北偏东30°方向上，15 min后到点B处望见灯塔在船的北偏东75°方向上，则船在点B时与灯塔S的距离是3km.‎ 解析：如图，由条件知，‎ AB＝24×＝6.‎ 8‎ 在△ABS中，∠BAS＝30°，AB＝6，∠ABS＝180°－75°＝105°，‎ ‎∴∠ASB＝45°.‎ 由正弦定理，得＝，‎ ‎∴BS＝＝3.‎ 三、解答题 ‎10．某人在塔的正东沿着南偏西60°的方向前进40 m后，望见塔在东北方向，若沿途测得塔的最大仰角为30°，求塔高．‎ 解：设B为塔正东方向一点，AE为塔，沿南偏西60°行走40 m后到达C处，即BC＝40，‎ 且∠CAB＝135°，∠ABC＝30°.‎ 如图在△ABC中，‎ ＝，即＝.‎ ‎∴AC＝20.‎ 由点A向BC作垂线AG，此时仰角∠AGE最大等于30°.‎ 在△ABC中，∠ACB＝180°－135°－30°＝15°，‎ AG＝ACsin15°＝20sin15°＝10(－1)．‎ ‎∴AE＝AG·tan30°＝.‎ 即塔高为 m.‎ ‎11．某单位有A，B，C三个工作点，需要建立一个公共无线网络发射点O，使得发射点到三个工作点的距离相等．已知AB＝80 m，BC＝70 m，CA＝50 m．假定A，B，C，O四点在同一平面内．‎ ‎(1)求∠BAC的大小；‎ ‎(2)求点O到直线BC的距离．‎ 解：(1)在△ABC中，因为AB＝80 m，BC＝70 m，CA＝50 m，所以由余弦定理得 cos∠BAC＝＝＝.‎ 因为∠BAC为△ABC的内角，所以∠BAC＝.‎ 8‎ ‎(2)设△ABC外接圆的半径为R，由(1)知A＝，‎ 所以sinA＝，由正弦定理得2R＝＝＝，即R＝.‎ 过点O作边BC的垂线，垂足为D，‎ 在Rt△OBD中，OB＝R＝，BD＝＝35，‎ 所以OD＝＝＝，‎ 所以点O到直线BC的距离为 m.‎ ‎——能力提升类——‎ ‎12．如图所示，在地面上共线的三点A，B，C处测得一建筑物的仰角分别为30°，45°，60°，且AB＝BC＝60 m，则建筑物的高度为(　D　)‎ A．15 m B．20 m C．25 m D．30 m 解析：设建筑物的高度为h m，由题图知，PA＝2h m，PB＝h m，PC＝h m，∴在△PBA和△PBC中，分别由余弦定理，得cos∠PBA＝，①‎ cos∠PBC＝.②‎ ‎∵∠PBA＋∠PBC＝180°，‎ ‎∴cos∠PBA＋cos∠PBC＝0.③‎ 由①②③，解得h＝30或h＝－30(舍去)，‎ 即建筑物的高度为30 m.‎ ‎13.如下图所示，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高度是60 m，则河流的宽度BC等于(　C　)‎ 8‎ A．240(－1) m B．180(－1) m C．120(－1) m D．30(＋1) m 解析：由题意可知，AC＝＝120.因为∠BAC＝75°－30°＝45°，∠ABC＝180°－45°－30°＝105°，所以sin∠ABC＝sin105°＝sin(60°＋45°)＝sin60°cos45°＋cos60°sin45°＝.在△ABC中，由正弦定理得＝，所以BC＝＝＝120(－1)．‎ ‎14．一只蜘蛛沿东北方向爬行x cm捕捉到一只小虫，然后向右转105°，爬行10 cm捕捉到另一只小虫，这时它向右转135°爬行回它的出发点，那么x＝.‎ 解析：如图所示，设蜘蛛原来在O点，先爬行到A点，再爬行到B点，易知在△AOB中，AB＝10 cm，∠OAB＝75°，∠ABO＝45°，‎ 则∠AOB＝60°.由正弦定理知：‎ x＝＝＝(cm)．‎ ‎15．在海岛A上有一座海拔1 km的山峰，山顶设有一个观察站P.有一艘船按一固定方向做匀速直线航行，上午11：00时，测得此船在岛北偏东15°，俯角为30°的B处，到11：10时，又测得该船在岛北偏西45°且俯角为60°的C处．‎ ‎(1)求船的航行速度；‎ ‎(2)求船从B到C的行驶过程中与观察站P的最短距离．‎ 解：(1)如图，在Rt△PAB中，∠PBA＝30°，‎ ‎∴AB＝＝(km)．‎ 8‎ 同理，在Rt△PCA中，AC＝＝(km)．‎ 在△ACB中，∠CAB＝15°＋45°＝60°，‎ ‎∴由余弦定理得BC＝‎ ＝(km)，‎ ‎∴÷＝2 (km/h)，‎ ‎∴船的航行速度为2 km/h.‎ ‎(2)作AD⊥BC于点D，连接PD.当船行驶到D时，离A点距离最小，从而离P点距离最小．此时，cos∠CBA＝＝＝，‎ ‎∴sin∠CBA＝，即＝，∴AD＝(km)．‎ ‎∴PD＝＝ (km)．‎ 即船在行驶过程中与观察站P的最短距离为 km.‎ 8‎