2020_2021学年新教材高中数学第五章三角函数5 38页

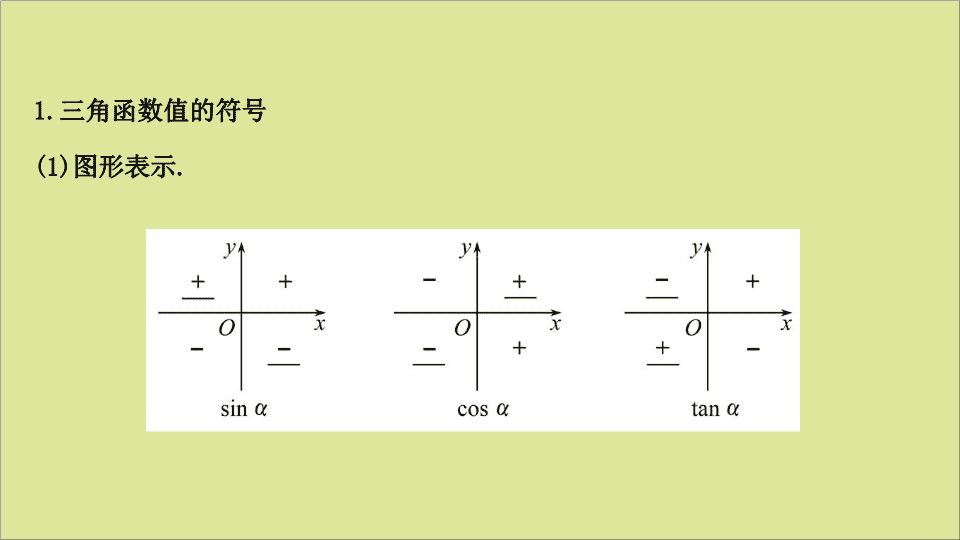
5.2.1 　三角函数的概念 ( 二 ) 　 必备知识 · 自主学习 1. 三角函数值的符号 (1) 图形表示 . (2) 记忆口诀：一全正、二正弦、三正切、四余弦 . (3) 本质：三角函数值在各个象限内的符号，是根据单位圆与角的终边在各个象限内的交点坐标的符号决定的 . (4) 应用：根据三角函数值在各个象限内的符号，可以在不求三角函数值的情况下，判断三角函数的正负 . 2. 公式一 (1) 公式： sin(α+k·2π)=_______ ， cos(α+k·2π)=_______ ， tan(α+k·2π)=_______(k∈Z).  (2) 本质：终边相同的角的终边与单位圆交点相同，因此同一三角函数值相等 . (3) 应用：将角的三角函数转化为终边相同的特殊角的同一三角函数求值 . sin α cos α tan α 【 思考 】 根据三角函数的公式一，终边相同的角的同一三角函数值有何关系？ 提示： 终边相同的角，其同一三角函数的值相等 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 已知 α 是三角形的内角，则必有 cos α>0. ( 　　 ) (2) 终边相同的角的同一三角函数值相等 . ( 　　 ) (3) 若 sin α>0 ，则 α 一定在第一或第二象限 . ( 　　 ) 提示： (1) ×. 当 α 为钝角时， cos α<0. (2) √. (3) ×. 终边落在 y 轴的非负半轴上，也有 sin α>0. 2. 若 sin θ·cos θ>0 ，则角 θ 在 ( 　　 ) A. 第一或第四象限 B. 第一或第三象限 C. 第一或第二象限 D. 第二或第四象限 【 解析 】 选 B. 因为 sin θ · cos θ>0 ，所以 sin θ>0 ， cos θ>0 或 sin θ<0 ， cos θ<0 ，所以角 θ 在第一象限或第三象限 . 3.( 教材二次开发：例题改编 )sin(-315°) 的值是 ( 　　 ) 【 解析 】 选 C.sin(-315°)=sin(-360°+45°)=sin 45°= . 关键能力 · 合作学习 类型一　三角函数值符号的应用 ( 数学抽象、直观想象 ) 【 题组训练 】 1.(2020 · 珠海高一检测 ) 已知点 M(sin θ ， tan θ) 在第三象限，则角 θ 在 ( 　　 ) A. 第一象限　　　　　　　 B. 第二象限 C. 第三象限 D. 第四象限 2.(2020 · 南宁高一检测 ) 若 sin α·cos α<0 ，则角 α 的终边在 ( 　　 ) A. 第一或第二象限 B. 第一或第三象限 C. 第一或第四象限 D. 第二或第四象限 3. 判断下列各式的符号： ① tan 191°-cos 191° ； ② sin 3·cos 4·tan 5. 【 解析 】 1. 选 D. 因为点 M(sin θ ， tan θ) 在第三象限，所以 由①知， θ 为第三象限、第四象限或 y 轴非正半轴上的角； 由②知， θ 为第二或第四象限角 . 综上，角 θ 在第四象限 . 2. 选 D. 因为 sin α · cos α<0 ，则 sin α>0 ， cos α<0 或 sin α<0 ， cos α>0. 若 sin α>0 ， cos α<0 ，则角 α 的终边在第二象限 . 若 sin α<0 ， cos α>0 ， 则角 α 的终边在第四象限 . 综上，角 α 的终边在第二或第四象限 . 3.① 正；因为 191° 是第三象限角； 所以 tan 191°>0 ， cos 191°<0. 所以 tan 191°-cos 191°>0. ② 正；因为 <3<π ， π<4< ， <5<2π ， 所以 sin 3>0 ， cos 4<0 ， tan 5<0 ， 所以 sin 3 · cos 4 · tan 5>0. 【 解题策略 】 判断三角函数的符号的常用方法 (1) 定象限：根据题目给出的条件，确定角所在的象限 . (2) 定符号：根据角所在象限，结合题目的具体特点，最终确定符号 . 【 补偿训练 】 已知角 α 的终边过点 (3a-9 ， a+2) ，且 cos α≤0 ， sin α>0 ， 则实数 a 的取值范围是 _______.  【 解析 】 因为 cos α≤0 ， sin α>0 ，所以角 α 的终边在第二象限或 y 轴非负 半轴上，因为 α 终边过 (3a-9 ， a+2) ，所以 所以 -20.② 由①②得角 α 在第四象限 . (2) 因为点 M 在单位圆上， 所以 +m 2 =1 ，解得 m=± . 又角 α 是第四象限角， 所以 m<0 ，所以 m= . 由三角函数定义知， sin α= . 所以 sin(α+6π)=sin α= . 【 解题策略 】 三角函数求值与角的终边相关联 (1) 角 α 的三角函数值的符号只与角 α 所在象限有关，角 α 所在象限确定，则三角函数值的符号一定确定 . (2) 终边相同的三角函数值一定相等，但两个角的某一个函数值相等，不一定有角的终边相同，更不一定有两角相等 . 【 题组训练 】 1. 若三角形的两内角 α ， β 满足 sin αcos β<0 ，则此三角形必为 ( 　　 ) A. 锐角三角形　　　　　　 B. 钝角三角形 C. 直角三角形 D. 以上三种情况都可能 【 解析 】 选 B. 因为 sin αcos β<0 ， α ， β∈(0 ， π) ， 所以 sin α>0 ， cos β<0 ，所以 β 为钝角 . 2. 已知 α∈ 且 sin α>0 ，则下列不等式一定成立的是 ( 　　 ) A.cos α·tan α<0 B.sin α·tan α>0 C.cos α-tan α<0 D.sin α-tan α>0 【 解析 】 选 D. 已知 α∈ 且 sin α>0 ，则 α∈ ，所以 cos α<0 ， tan α<0. 所以对于选项 A ： cos α · tan α>0 ，故选项 A 错误 . 对于选项 B ： sin α · tan α<0 ，故选项 B 错误 . 对于选项 C ： cos α-tan α 不能确定符号，故选项 C 错误 . 对于选项 D ： sin α-tan α>0 ，故选项 D 正确 . 3. 使得 lg(cos αtan α) 有意义的角 α 是第 _______ 象限角 .  【 解析 】 要使原式有意义，必须 cos αtan α>0 ，即需 cos α ， tan α 同号，所以 α 是第一或第二象限角 . 答案： 一或二 【 补偿训练 】 若 tan x<0 ，且 sin x-cos x<0 ，则角 x 的终边在 ( 　　 ) A. 第一象限　　　　　　 B. 第二象限 C. 第三象限 D. 第四象限 【 解析 】 选 D. 因为 tan x<0 ，所以角 x 的终边在第二、四象限，又 sin x-cos x <0 ，所以角 x 的终边在第四象限 . 三角函数的 概念（二） 弧度制给出的角应转化成角度制，再判断其三角函数值的符号 利用三角函数定义求三角函数值题型：（ 1 ）已知角终边上的点求三角函数值；（ 2 ）已知角终边的位置求三角函数值； （ 3 ）已知三角函数值求参数 三角函数的定义 三角函数值的符号 坐标法 单位圆法 诱导公式（一） 核心知识 方法总结 易错提醒 核心素养 数学运算：通过诱导公式（一）的应用，培养数学运算的核心素养 数学抽象：通过三角函数定义的引入，培养数学抽象的核心素养 课堂检测 · 素养达标 1. 若 cos α<0 ， tan α>0 ，则 α 在 ( 　　 ) A. 第一象限　　　　　 B. 第二象限 C. 第三象限 D. 第四象限 【 解析 】 选 C. 由余弦、正切函数值在各象限内的符号知，角 α 是第三象限角 . 2.cos(-1 410°) 的值为 ( 　　 ) 【 解析 】 选 C.cos(-1 410°)=cos(-4×360°+30°)=cos 30°= . 3.( 教材二次开发：练习改编 ) 设△ ABC 的三个内角为 A ， B ， C ，则下列各组数 中有意义且均为正值的是 ( 　　 ) A.tan A 与 cos B 　　　　　 B.cos B 与 sin C C.sin C 与 tan A D.tan 与 sin C 【 解析 】 选 D. 因为 00 ；又因为 00. 4.sin =_______.  【 解析 】 答案： 5. 判断下列各式的符号 ( 填上“ >” 或“ <”) ： (1)sin328°_______0.(2)cos π_______0.(3)tan π_______0.  【 解析 】 (1) 因为 270°<328°<360° ，所以 328° 在第四象限，所以 sin 328°<0. (2) 因为 π< ，所以 π 在第三象限， 所以 cos π<0. (3) 因为 <π ，所以 π 在第二象限， 所以 tan π<0. 答案： (1)< 　 (2)< 　 (3)<