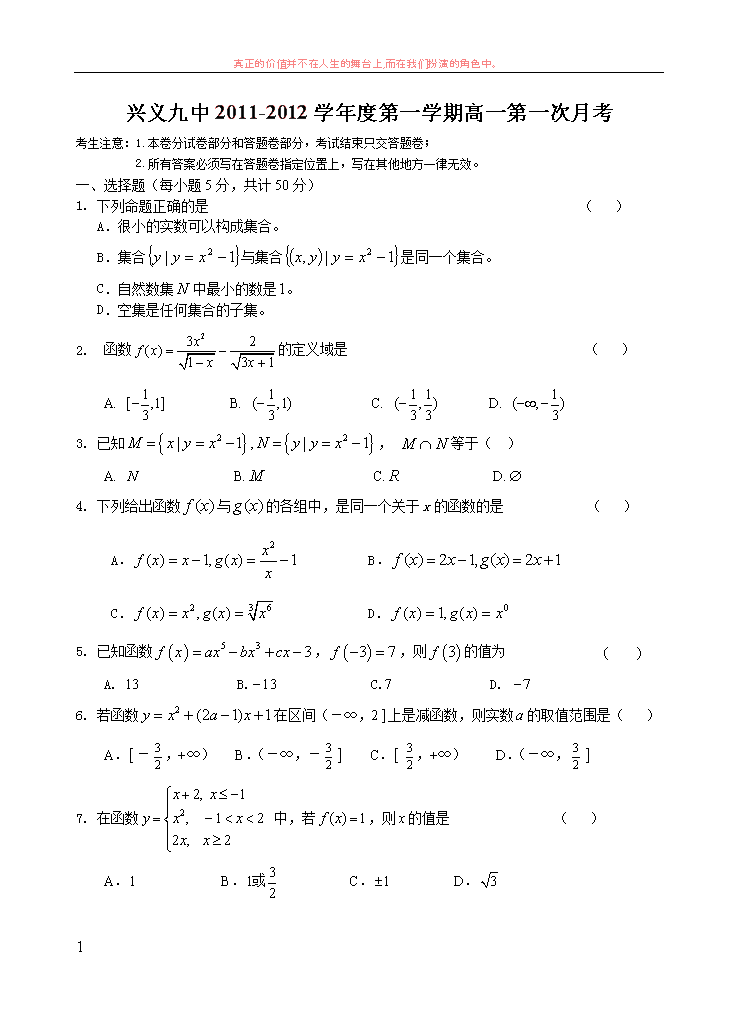高一数学必修一第一次月考及答案 12页

真正的价值并不在人生的舞台上,而在我们扮演的角色中。 1 兴义九中 2011-2012 学年度第一学期高一第一次月考 考生注意：1.本卷分试卷部分和答题卷部分，考试结束只交答题卷； 2.所有答案必须写在答题卷指定位置上，写在其他地方一律无效。 一、选择题（每小题 5 分，共计 50 分） 1. 下列命题正确的是 （ ） A．很小的实数可以构成集合。 B．集合 1| 2  xyy 与集合   1|, 2  xyyx 是同一个集合。 C．自然数集 N 中最小的数是1。 D．空集是任何集合的子集。 2. 函数 23 2( ) 1 3 1     xf x x x 的定义域是 （ ） A. 1[ ,1] 3  B. 1( ,1) 3  C. 1 1( , ) 3 3  D. 1( , ) 3   3. 已知    2 2| 1 , | 1     M x y x N y y x ， NM  等于（ ） A. N B.M C. R D. 4. 下列给出函数 ( )f x 与 ( )g x 的各组中，是同一个关于 x 的函数的是 （ ） A． 2 ( ) 1, ( ) 1xf x x g x x     B． ( ) 2 1, ( ) 2 1f x x g x x    C． 32 6( ) , ( )f x x g x x  D． 0( ) 1, ( )f x g x x  5. 已知函数   5 3 3f x ax bx cx    ，  3 7f   ，则  3f 的值为 ( ) A. 13 B. 13 C.7 D. 7 6. 若函数 2 (2 1) 1   y x a x 在区间（－∞，2 ]上是减函数，则实数 a的取值范围是（ ） A．[ － 2 3 ，+∞） B．（－∞，－ 2 3 ] C．[ 2 3 ，+∞） D．（－∞， 2 3 ] 7. 在函数 2 2, 1 , 1 2 2 , 2 x x y x x x x          中，若 ( ) 1f x  ，则 x的值是 （ ） A．1 B． 31 2 或 C． 1 D． 3 8. 已知函数 2( ) 1  f x mx mx 的定义域是一切实数,则m的取值范围是 （ ） 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 2 B BAA U UU CBA A.00， 2 2( ) ( ) 2( ) 2f x x x x x        又 f（x）为奇函数，∴ 2( ) ( ) 2f x f x x x      ， ∴ f（x）＝x2＋2x，∴m＝2 ……………4 分 y＝f（x）的图象如右所示 ……………6 分 （2）由（1）知 f（x）＝ 2 2 2 ( 0) 0 ( 0) 2 ( 0) x x x x x x x         ，…8 分 由图象可知， ( )f x 在[－1，1]上单调递增，要使 ( )f x 在[－1，|a|－2]上单调递 增，只需 | | 2 1 | | 2 1 a a       ……………10 分 解之得 3 1 1 3a a     或 ……………12 分 21 解： 2 2( ) 2 ( )f x x ax a x a a a       ，对称轴 x a （1）当 1a  时，由题意得 ( )f x 在[ 1,1] 上是减函数 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 11 ( )f x 的值域为[1 ,1 3 ]a a  则有 1 2 1 3 2 a a       满足条件的 a不存在。 （2）当 0 1a  时，由定义域为[ 1,1] 知 ( )f x 的最大值为 ( 1) 1 3f a   。 ( )f x 的最小值为 2( )f a a a  2 1 3 2 2 a a a       1 3 2 1 a a a a        不存在 或 （3）当 1 0a   时，则 ( )f x 的最大值为 (1) 1f a  ， ( )f x 的最小值为 2( )f a a a  2 1 2 2 a a a       得 1a   满足条件 （4）当 1a   时，由题意得 ( )f x 在[ 1,1] 上是增函数 ( )f x 的值域为[1 3 ,1 ]a a  ，则有 1 3 2 1 2 a a       满足条件的 a不存在。 综上所述，存在 1a   满足条件。 22、（1）投资为 x万元，A产品的利润为 ( )f x 万元，B产品的利润为 ( )g x 万元， 由题设 ( )f x = 1k x ， ( )g x = 2k x ，. 由图知 1(1) 4 f   1 1 4 k  ，又 5(4) 2 g   2 5 4 k  从而 ( )f x = 1 , ( 0) 4 x x  ， ( )g x = 5 4 x， ( 0)x  ……………6 分 （2）设 A产品投入 x万元，则 B产品投入 10- x万元，设企业的利润为 y万元 Y= ( )f x + (10 )g x = 5 10 4 4 x x  ，（0 10x  ）， 令 2 210 5 1 5 2510 , ( ) , (0 10), 4 4 4 2 16 tx t y t t t          则 当 5 2 t  ， max 4y  ，此时 2510 4 x   =3.75 当 A产品投入 3.75 万元，B产品投入 6.25 万元时， 企业获得最大利润约为 4万元。 ……………12 分 真正的价值并不在人生的舞台上,而在我们扮演的角色中。 12