1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 高中数学必修1教案：第二章（第22课时）对数函数3

高中数学必修1教案：第二章（第22课时）对数函数3 5页

  • 254.00 KB
  • 2021-06-10 发布

高中数学必修1教案：第二章（第22课时）对数函数3

  • 5页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
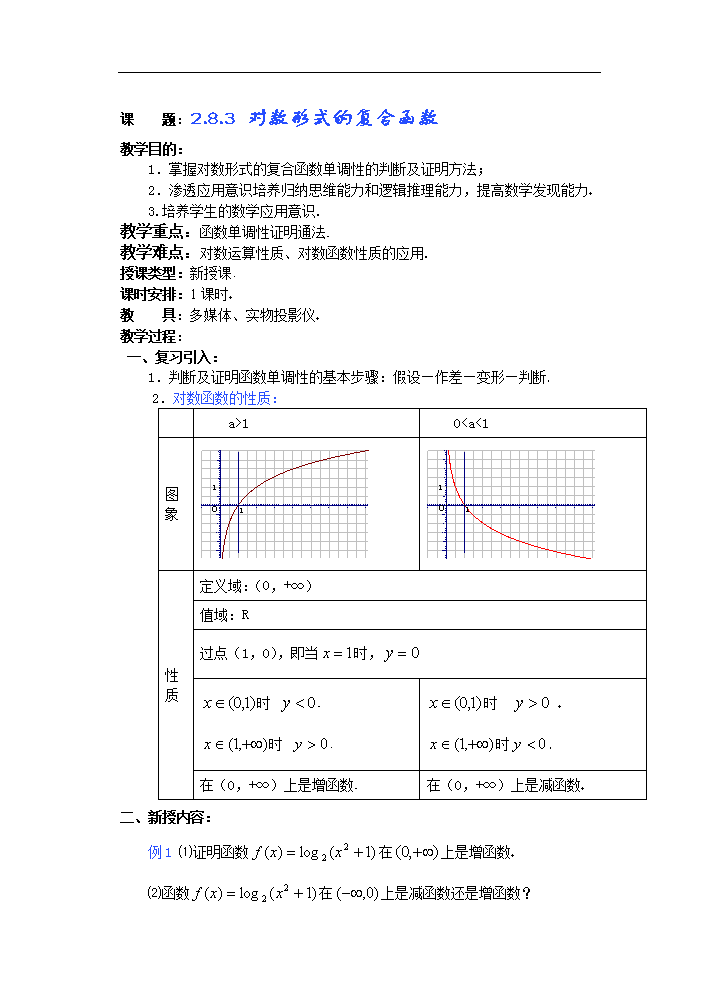
课 题：2.8.3 对数形式的复合函数 教学目的： ‎ ‎1．掌握对数形式的复合函数单调性的判断及证明方法；‎ ‎2．渗透应用意识培养归纳思维能力和逻辑推理能力，提高数学发现能力 ‎3.培养学生的数学应用意识.‎ 教学重点：函数单调性证明通法 教学难点：对数运算性质、对数函数性质的应用.‎ 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程： ‎ 一、复习引入：‎ ‎1．判断及证明函数单调性的基本步骤：假设—作差—变形—判断 ‎2．对数函数的性质：‎ a>1‎ ‎0 又底数 ‎ ‎∴ 即 ‎ ‎∴在上是减函数 同理可证：在上是增函数 三、练习：‎ ‎1.求y=(-2x)的单调递减区间 解：先求定义域：由-2x＞0,得x(x-2)＞0‎ ‎∴x＜0或x＞2‎ ‎∵函数y=t是减函数 故所求单调减区间即t=-2x在定义域内的增区间 又t=-2x的对称轴为x=1‎ ‎∴所求单调递减区间为（2，+∞）‎ ‎2.求函数y=(-4x)的单调递增区间 解：先求定义域：由-4x＞0得x(x-4)＞0‎ ‎∴x＜0或x＞4‎ 又函数y=t是增函数 故所求单调递增区间为t=-4x在定义域内的单调递增区间 ‎∵t=-4x的对称轴为x=2‎ ‎∴所求单调递增区间为：（4，+∞）‎ ‎3.已知y=(2-)在［0，1］上是x的减函数，求a的取值范围.‎ 解：∵a＞0且a≠1‎ 当a＞1时，函数t=2->0是减函数 由y= (2-)在［0，1］上x的减函数，知y=t是增函数，‎ ‎∴a＞1‎ 由x［0，1］时，2-2-a＞0,得a＜2,‎ ‎∴1＜a＜2‎ 当00是增函数 由y= (2-)在［0，1］上x的减函数，知y=t是减函数，‎ ‎∴0

您可能关注的文档

相关文档

最近下载