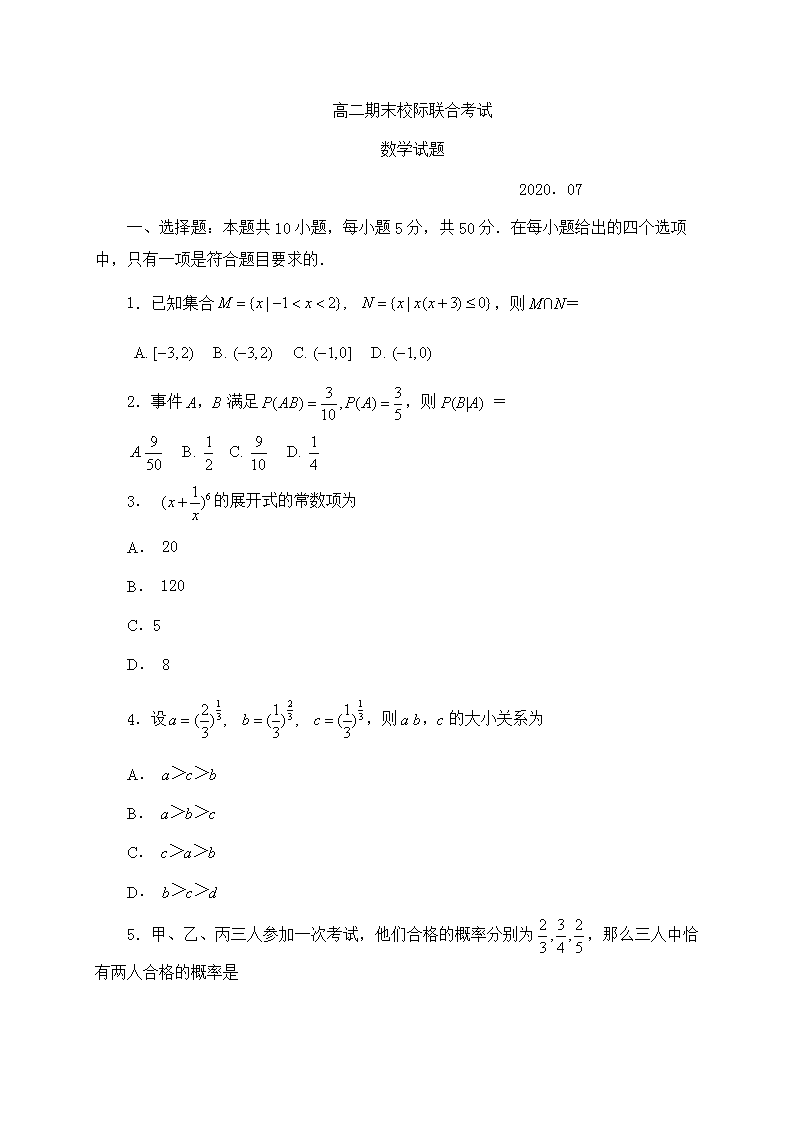山东省日照市2019-2020学年高二下学期期末校际联合考试数学试题 Word版含答案 17页

高二期末校际联合考试 数学试题 ‎2020．07‎ 一、选择题：本题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，则M∩N＝‎ ‎2．事件A，B满足，则P(B|A) ＝‎ ‎3． 的展开式的常数项为 A． 20‎ B． 120‎ C．5‎ D． 8‎ ‎4．设，则a b，c的大小关系为 A． a＞c＞b B． a＞b＞c C． c＞a＞b D． b＞c＞d ‎5．甲、乙、丙三人参加一次考试，他们合格的概率分别为，那么三人中恰有两人合格的概率是 ‎6．已知变量X， Y之间具有线性相关关系，若通过10组数据得到的回归方程为，且，则 A．2 B． 2．1 C． －2．1 D．－2‎ ‎7．万历十二年，中国明代音乐理论家和数学家朱载堉在其著作《律学新说》中，首次用珠算开方的办法计算出了十二个半音音阶的半音比例，这十二个半音音阶称为十二平均律十二平均律包括六个阳律（黄钟、太簇、姑洗、蕤宾、夷则、无射）和六个阴律（大吕、夹钟、中吕、林钟、南吕、应钟）．现从这十二平均律中取出2个阳律和2个阴律，排成一个序列，组成一种旋律，要求序列中的两个阳律相邻，两个阴律不相邻，则可组成不同的旋律 A． 450种 B． 900种 C． 1350种 D． 1800种 ‎8．函数的图象大致是 ‎9．已知函数在（1，3）内不是单调函数，则实数a的取值范围是 ‎10．若函数的值域为R，则m的取值范围为 二、选择题：本题共4小题，每小题5分，共20分》在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得3分，有选错的得0分．‎ ‎11． 若a＞b＞0，则 ‎12．2019年10月31日，工信部宣布全国5G商用正式启动，三大运营商公布5G套餐方案，中国正式跨入5G时代．某通信行业咨询机构对包括我国三大5G设备商进行了全面评估和比较，其结果如雷达图所示（每项指标值满分为5分，分值高者为优），则 A． P设备商的研发投入超过Q设备商与R设备商 B．三家设备商的产品组合指标得分相同 C．在参与评估的各项指标中， Q设备商均优于R ‎ 设备商 D．除产品组合外， P设备商其他4项指标均超过 Q设备商与R设备商 ‎13．已知函数f（x）是定义域为（－¥， ＋¥）的奇函数，函数f（x＋1）是偶函数，且当时， f（x）＝－x（x－2），则 A．函数f（x）是以2为周期的周期函数 B． f(2019) ＋f(2020) ＝－1‎ C．函数f(x)的值域为[－1，1]‎ D．函数f（x）的图象与曲线y＝cosx在（0，2π）上有4个交点 ‎14．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x∈R，用[x]表示不超过x的最大整数，则y＝[x]称为高斯函数，例如： [－3．5]＝4， [2．1]＝2．已知函数，则关于函数g（x）＝[f（x）]的叙述中正确的是 A． g（x）是偶函数 B．f（x）是奇函数 C．g(x)的值域是 D． g（x）在R上是增函数 三、填空题：本题共4小题，每小题5分，共20分．‎ ‎15．若随机变量 ，且，则________‎ ‎16．函数f（x）是定义在R上的奇函数，，当x＜0时，，则实数m＝________‎ ‎17．十六、十七世纪之交，随着天文、航海、工程、贸易及军事的发展，约翰·纳皮尔在研究天文学的过程中，为了简化其中的计算而发明了对数，改进了数字计算方法．后来天才数学家欧拉发现了对数与指数的关系，即．现已知，则________‎ ‎（第一空答对2分，第二空答对3分）‎ ‎18．已知函数，若，使得成立，则a的取值范围为________‎ 四、解答题：本题共5小题，共60分．解答应写出必要的文字说明、证明过程或演算步骤．‎ ‎19． （12 分）‎ 已知函数在点（1，f（1））处的切线与直线4x＋y—5＝0平行． ‎ ‎(1)求a的值；‎ ‎(2)求函数f(x)在区间[－4，4]的最大值和最小值．‎ ‎20． (12分) ‎ ‎2020年5月1日起，《北京市垃圾分类管理条例》正式实施，某社区随机对200种垃圾分类能否辨识进行了随机调查，经整理得到下表：‎ 辨识率是指：一类垃圾中能辨识种类的数量与该类垃圾的种类总数的比值．‎ ‎（1）从社区调查的200种垃圾中随机选取一种，求这种垃圾能辨识的概率；‎ ‎（2）从可回收物中有放回的抽取三种垃圾，记 X为其中能辨识的垃圾种数，求X的分布列和数学期望．‎ ‎21． (12 分)‎ 设函数，且函数f（x）的图象关于直线x＝1对称 ‎（1）求函数f（x）在区间[0，4]上的最小值；‎ ‎（2）设，不等式在x∈ [－1，1]上恒成立，求实数k的取值范围．‎ ‎22． （12分）‎ 某种疾病可分为Ⅰ、Ⅱ两种类型，为了解该疾病类型与性别的关系，在某地区随机抽取了患该疾病的病人进行调查，其中男性人数为z，女性人数为2z，男性患Ⅰ型病的人数占男性病人的，女性患Ⅰ型病的人数占女性病人的．‎ ‎（1）完成2x2联表若在犯错误的概率不超过 ‎0．005的前提下认为“所患疾病类型”与“性别”有关， ‎ 求男性患者至少有多少人？‎ ‎（2）某药品研发公司欲安排甲乙两个研发团队来研 发此疾病的治疗药物，两个团队各至多安排2个接种周期进行试验．每人每次接种花费m（m＞0）元．甲团队研发的药物每次接种后产生抗体的概率为p，根据以往试验统计，甲团队平均花费为；乙团队研发的药物每次接种后产生抗体的概率为q，每个周期必须完成3次接种，若一个周期内至少出现2次抗体，则该周期结束后终止试验，否则进入第二个接种周期．假设两个研发团队每次接种后产生抗体与否均相互独立．‎ 若p＝2q，从两个团队试验的平均花费考虑，该公司应选择哪个团队进行药品研发？‎ 附：‎ ‎ ‎ ‎23． （12分）‎ 已知 ‎（1）求f（x）的单调区间；‎ ‎（2）记F（x）＝f（x）－g（x），若函数F（x）存在两个零点，求实数a的取值范围．‎