1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 高二数学人教a必修5练习：第一章解三角形章末复习课word版含解析

高二数学人教a必修5练习：第一章解三角形章末复习课word版含解析 4页

  • 187.48 KB
  • 2021-06-11 发布

高二数学人教a必修5练习：第一章解三角形章末复习课word版含解析

  • 4页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
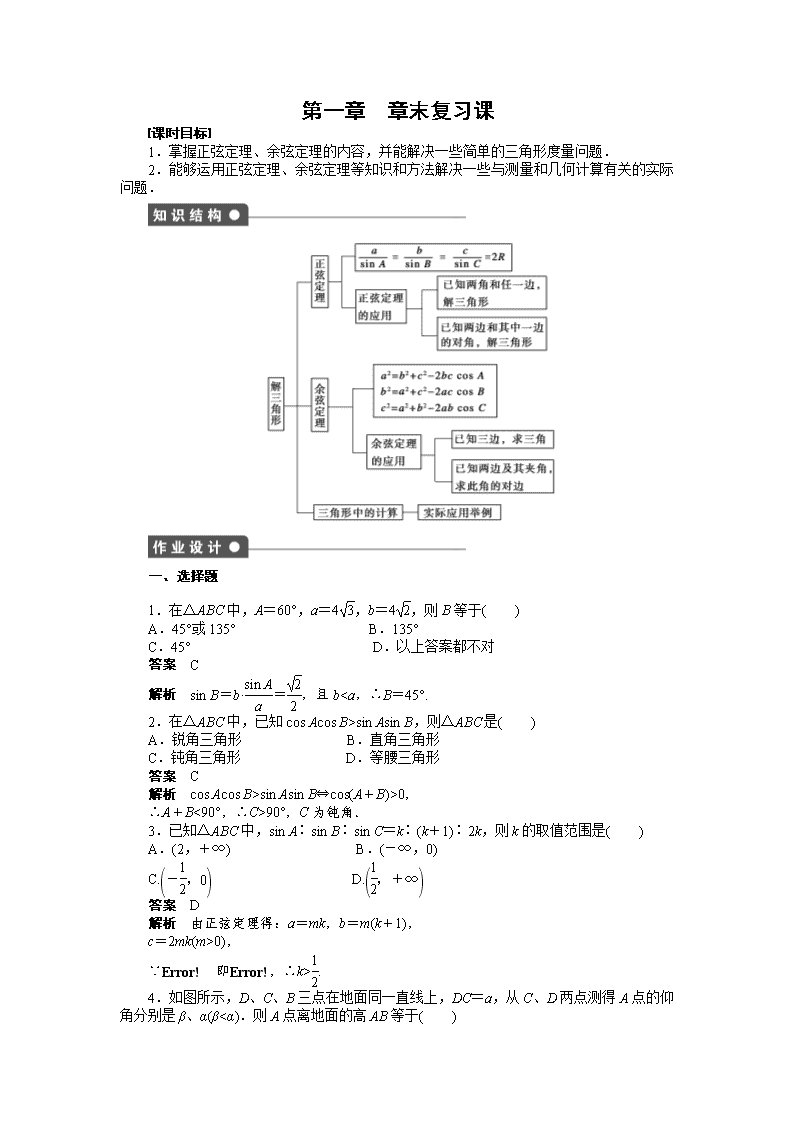
第一章 章末复习课 课时目标 1．掌握正弦定理、余弦定理的内容，并能解决一些简单的三角形度量问题． 2．能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际 问题． 一、选择题 1．在△ABC 中，A＝60°，a＝4 3，b＝4 2，则 B 等于( ) A．45°或 135° B．135° C．45° D．以上答案都不对 答案 C 解析 sin B＝b·sin A a ＝ 2 2 ，且 bsin Asin B，则△ABC 是( ) A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形 答案 C 解析 cos Acos B>sin Asin B⇔cos(A＋B)>0， ∴A＋B<90°，∴C>90°，C 为钝角． 3．已知△ABC 中，sin A∶sin B∶sin C＝k∶(k＋1)∶2k，则 k 的取值范围是( ) A．(2，＋∞) B．(－∞，0) C. －1 2 ，0 D. 1 2 ，＋∞ 答案 D 解析 由正弦定理得：a＝mk，b＝m(k＋1)， c＝2mk(m>0)， ∵ a＋b>c a＋c>b 即 m2k＋1>2mk 3mk>mk＋1 ，∴k>1 2. 4．如图所示，D、C、B 三点在地面同一直线上，DC＝a，从 C、D 两点测得 A 点的仰 角分别是β、α(β<α)．则 A 点离地面的高 AB 等于( ) A.asin αsin β sinα－β B.asin αsin β cosα－β C.asin αcos β sinα－β D.acos αcos β cosα－β 答案 A 解析 设 AB＝h，则 AD＝ h sin α ， 在△ACD 中，∵∠CAD＝α－β，∴ CD sinα－β ＝ AD sin β. ∴ a sinα－β ＝ h sin αsin β ，∴h＝asin αsin β sinα－β . 5．在△ABC 中，A＝60°，AC＝16，面积为 220 3，那么 BC 的长度为( ) A．25 B．51 C．49 3 D．49 答案 D 解析 S△ABC＝1 2AC·AB·sin 60°＝1 2 ×16×AB× 3 2 ＝220 3，∴AB＝55. ∴BC2＝AB2＋AC2－2AB·ACcos 60°＝552＋162－2×16×55×1 2 ＝2 401. ∴BC＝49. 6．(2010·天津)在△ABC 中，内角 A，B，C 的对边分别是 a，b，c.若 a2－b2＝ 3bc， sin C＝2 3sin B，则 A 等于( ) A．30° B．60° C．120° D．150° 答案 A 解析 由 sin C＝2 3sin B，根据正弦定理，得 c＝2 3b，把它代入 a2－b2＝ 3bc 得 a2－b2＝6b2，即 a2＝7b2. 由余弦定理，得 cos A＝b2＋c2－a2 2bc ＝b2＋12b2－7b2 2b·2 3b ＝ 6b2 4 3b2 ＝ 3 2 . 又∵0°1，不合题意．∴设夹角为θ，则 cos θ＝－3 5 ， 得 sin θ＝4 5 ，∴S＝1 2 ×3×5×4 5 ＝6 (cm2)． 8．在△ABC 中，A＝60°，b＝1，S△ABC＝ 3，则 a sin A ＝____________. 答案 2 39 3 解析 由 S＝1 2bcsin A＝1 2 ×1×c× 3 2 ＝ 3，∴c＝4. ∴a＝ b2＋c2－2bccos A＝ 12＋42－2×1×4cos 60° ＝ 13. ∴ a sin A ＝ 13 sin 60° ＝2 39 3 . 9．在△ABC 中，a＝x，b＝2，B＝45°，若三角形有两解，则 x 的取值范围是 ______________． 答案 2n＋2，∴n＝2. ∴cos θ＝4＋9－16 2×2×3 ＝－1 4. (2)设此平行四边形的一边长为 a，则夹θ角的另一边长为 4－a，平行四边形的面积为： S＝a(4－a)·sin θ＝ 15 4 (4a－a2)＝ 15 4 [－(a－2)2＋4]≤ 15. 当且仅当 a＝2 时，Smax＝ 15. 能力提升 13．在△ABC 中，角 A，B，C 所对的边分别为 a，b，c，已知 cos 2C＝－1 4. (1)求 sin C 的值； (2)当 a＝2,2sin A＝sin C 时，求 b 及 c 的长． 解 (1)∵cos 2C＝1－2sin2C＝－1 4 ，00)， 解得 b＝ 6或 2 6， ∴ b＝ 6， c＝4 或 b＝2 6， c＝4. 14．如图所示，已知在四边形 ABCD 中，AD⊥CD，AD＝10，AB＝14，∠BDA＝60°， ∠BCD＝135°，求 BC 的长． 解 设 BD＝x，在△ABD 中，由余弦定理有 AB2＝AD2＋BD2－2AD·BD·cos∠ADB， 即 142＝x2＋102－20xcos 60°， ∴x2－10x－96＝0，∴x＝16(x＝－6 舍去)， 即 BD＝16. 在△BCD 中，由正弦定理 BC sin∠CDB ＝ BD sin∠BCD ， ∴BC＝16sin 30° sin 135° ＝8 2. 1．在解三角形时，常常将正弦定理、余弦定理结合在一起用，要注意恰当的选取定理， 简化运算过程． 2．应用正、余弦定理解应用题时，要注意先画出平面几何图形或立体图形，再转化为 解三角形问题求解，即先建立数学模型，再求解．

您可能关注的文档

相关文档

最近下载