高一数学教案：第9讲 期中备考复习 10页

辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 期中备考复习 教学内容 ‎1. 熟练掌握对数函数的性质；‎ ‎2. 会应用对数函数的图像与性质解决综合问题。‎ 一、指对数函数：‎ ‎1. 若函数y=f(x)的定义域是[－1,1],则函数y=f(lgx－1)的定义域是 （ ） C ‎(A)(0,＋∞) (B)(0,100] (C)[1,100] (D)[2,＋∞)‎ ‎2. 函数的定义域是 （ ） D ‎(A)(－1,0) (B)(0,log45) (C)(－1,log45) (D) (－1,0)∪(0,log45)‎ ‎3. 函数的值域是（ ） B ‎(A) (B)[0,1] (C)[0,＋∞) (D){0}‎ ‎4. 若函数f(x)的定义域是[0,1),则F(x)=的定义域为（ ） B ‎(A)[0,1) (B)[2,) (C)[0,) (D)(－∞,3)‎ 此部分让学生回答，如出现学生不会的问题，可相互讨论，结合教师引导，5到10分钟完成。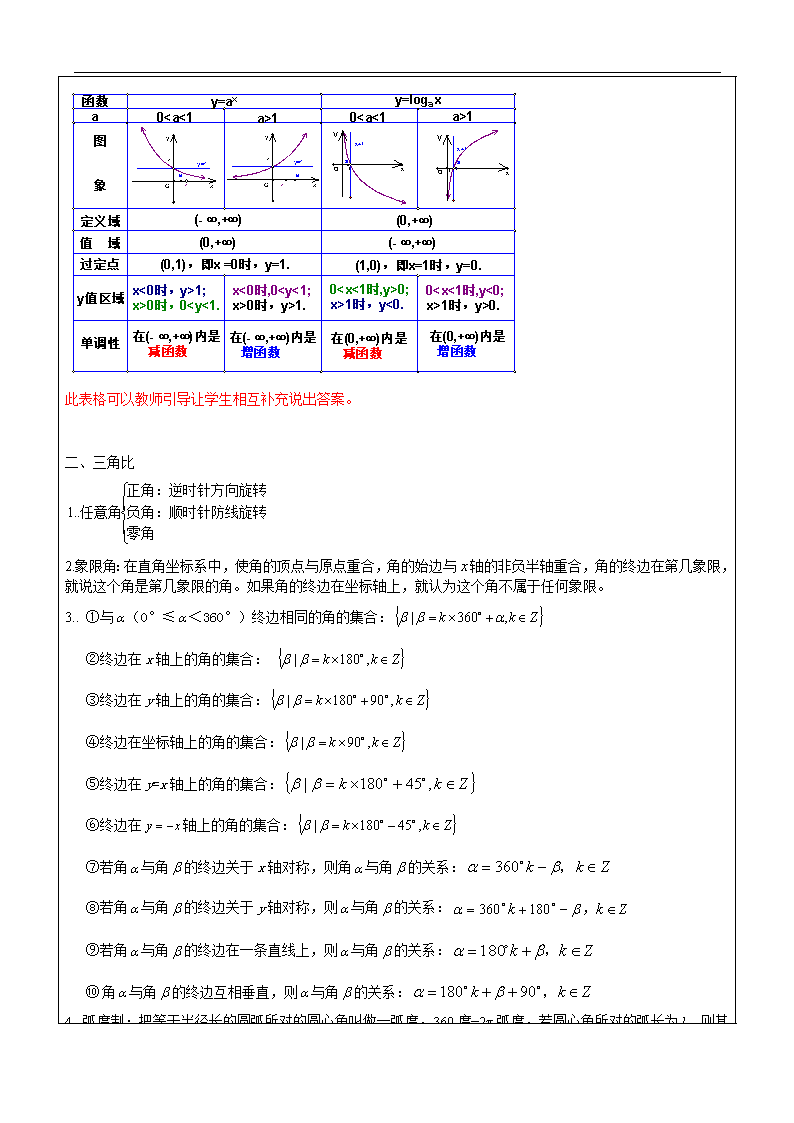‎ ‎5. 指数函数与对数函数的图象与性质 此表格可以教师引导让学生相互补充说出答案。‎ 二、三角比 ‎2.象限角：在直角坐标系中，使角的顶点与原点重合，角的始边与轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限的角。如果角的终边在坐标轴上，就认为这个角不属于任何象限。‎ ‎3.. ①与（0°≤＜360°）终边相同的角的集合：‎ ②终边在x轴上的角的集合： ‎ ③终边在y轴上的角的集合：‎ ④终边在坐标轴上的角的集合： ‎ ⑤终边在y=x轴上的角的集合： ‎ ⑥终边在轴上的角的集合：‎ ⑦若角与角的终边关于x轴对称，则角与角的关系：‎ ⑧若角与角的终边关于y轴对称，则与角的关系：‎ ⑨若角与角的终边在一条直线上，则与角的关系：‎ ⑩角与角的终边互相垂直，则与角的关系：‎ ‎4. 弧度制：把等于半径长的圆弧所对的圆心角叫做一弧度。360度=2π弧度。若圆心角所对的弧长为l ‎，则其弧度数的绝对值|,其中r是圆的半径。‎ ‎5. 弧度与角度互换公式： 1rad＝（）°≈57.30° 1°＝‎ 注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.‎ ‎6.. 第一象限的角： ‎ 锐角： ； 小于的角：（包括负角和零角）‎ ‎7. 弧长公式： 扇形面积公式：‎ ‎8. 任意角的三角函数的定义：设是任意一个角，P是的终边上的任意一点（异于原点），它与原点的距离是，那么， ‎ ‎ 三角函数值只与角的大小有关，而与终边上点P的位置无关。‎ ‎9. 三角函数线 ‎ 正弦线：MP; 余弦线：OM; 正切线： AT.‎ ‎10. 三角函数在各象限的符号：（一全二正弦，三切四余弦）‎ ‎ ＋ 　＋ －　　＋　　　　－　　＋‎ ‎　　－　　　－　　　－　　＋　　　　＋　　－‎ ‎ ‎ ‎11. 同角三角函数的基本关系式：‎ ‎（1）平方关系：‎ ‎（2）商数关系：（用于切化弦）‎ ‎※平方关系一般为隐含条件，直接运用。注意“1”的代换 ‎12. 诱导公式（把角写成形式，利用口诀：奇变偶不变，符号看象限）‎ Ⅰ） Ⅱ） Ⅲ） ‎ Ⅳ） Ⅴ） Ⅵ）‎ ‎13. 两角和差展开公式 ‎ ‎ ‎ ‎ ‎ ‎ ‎14. 正弦、余弦和正切的二倍角：‎ ‎ ；‎ ‎ ；‎ ‎ ‎ ‎ ；‎ ‎．‎ ‎15. 半角公式：‎ ‎，，．‎ ‎16.万能公式：‎ ‎17. 正余弦定理：‎ ‎（R是三角形外接圆的半径）‎ ‎，，‎ 知识点梳理部分教师可针对学生薄弱点重点详细讲解，没有问题就一带而过。‎ 例1. 已知函数.‎ ‎（1）求的定义域、值域，并判断的单调性；‎ ‎（2）解不等式．‎ 解：（1）为使函数有意义，需满足，即，又，∴，即函数定义域为（﹣∞，1）．‎ 又由，，∴函数的值域为（﹣∞，1）．‎ 设，则 即． ∴在（﹣∞，1）上是减函数． ‎ ‎（2）设，则．‎ ‎∴的反函数为 由，得，‎ ‎∴ 解得． 故所求不等式的解为．‎ 例2. 求证：．‎ 证明：左边 ‎ ‎ ‎ ，‎ 右边．‎ 所以，原式成立。‎ 例3. 已知，求．‎ 解：由等式两边平方：‎ ‎∴（*），‎ 即， 因此 ‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ 1、 函数的反函数是____________‎ 2、 若对数式：有意义，则实数x的取值范围是_____________‎ ‎3、已知 ‎4、化简：‎ ‎5、若，则角的取值范围是_____________‎ ‎6、如果点既在函数的图像上，又在它的反函数的图像上，则实数 ‎7、方程的解为____________‎ ‎8、若角终边落在射线上,则 ‎9、已知扇形的周长为20厘米，当扇形的中心角为____________弧度时，扇形面积最大 ‎10、已知函数在区间上存在反函数，则实数的取值范围是______________‎ ‎11、设 ‎12、已知面积求 面积的最大值 ‎13、已知 求 ‎11.‎ ‎12. ‎ ‎ ‎ ‎13．‎ ‎ ‎ 本节课主要知识：复习指对数函数图像与性质，三角比公式 ‎ ‎【巩固练习】‎ ‎1. 已知求的值。‎ 解： ‎ ‎2.已知，，且，求 解： ‎ ‎ ‎ ‎，，又 ‎ ‎ ‎3. 如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援（角度精确到）？‎ 解法一： 连接BC,由余弦定理得 BC2=202+102－2×20×10cos120°=700.‎ ‎ 于是,BC=10.‎ ‎ ∵, ∴sin∠ACB=,‎ ‎ ∵∠ACB<90°, ∴∠ACB=41°.‎ ‎∴乙船应朝北偏东71°方向沿直线前往B处救援.‎ 解法二：BC2=202+102－2×20×10COS120°=700， ‎ 有此得，∴乙船应朝北偏东71°方向沿直线前往B处救援. ‎ ‎4. 已知,且,求的最小值。‎ 解：由已知,, ‎ ‎ ‎ ‎ 当时,的最小值为 ‎【预习思考】‎ ‎1. _____________________________________________________________________叫做周期函数，___________________________________________叫这个函数的周期.‎ ‎2. _____________________________________叫做函数的最小正周期.‎ ‎3.正弦函数，余弦函数都是周期函数，周期是____________，最小正周期是________.‎ ‎4.由诱导公式_________________________可知正弦函数是奇函数.由诱导公式_________________________可知，余弦函数是偶函数.‎ ‎5.正弦函数图象关于____________________对称，正弦函数是_____________.余弦函数图象关于________________对称，余弦函数是_____________________.‎ ‎6.正弦函数在每一个闭区间_________________上都是增函数，其值从－1增大到1；在每一个闭区间_________________上都是减函数，其值从1减少到－1.‎ ‎7.余弦函数在每一个闭区间_________________上都是增函数，其值从－1增大到1；在每一个闭区间______________上都是减函数，其值从1减少到－1.‎ ‎8.正弦函数当且仅当x＝___________时取得最大值1；当且仅当x=__________时取得最小值－1.‎ ‎9.余弦函数当且仅当x＝___________时取得最大值1；当且仅当x=__________时取得最小值－1.‎