2020年数学全国统一高考 数学试卷（文科）（新课标Ⅱ）【word版；可编辑；含答案】 10页

1 / 10 2020 年全国统一高考数学试卷（文科）（新课标Ⅱ） 一、选择题 1.已知集合퐴 = {푥||푥| < 3，푥 ∈ 퐙}，퐵 = {푥||푥| > 1，푥 ∈ 퐙}， 则퐴 ∩ 퐵 =() A.⌀ B.{−3， − 2，2，3} C.{−2，0，2} D.{−2，2} 2.(1 − 푖)4 =() A.−4 B.4 C.−4푖 D.4푖 3.如图，将钢琴上的12个键依次记为푎1，푎2，⋯，푎12，设1 ≤ 푖 ≤ 푗 ≤ 푘 ≤ 12．若푘 − 푗 = 3且푗 − 푖 = 4，则称푎푖，푎푗，푎푘为原位大 三和弦；若푘 − 푗 = 4且푗 − 푖 = 3，则称푎푖，푎푗，푎푘为原位小三和 弦．用这12个键可以构成的原位大三和弦与原位小三和弦的个数之 和为() A.5 B.8 C.10 D.15 4.在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天 能完成1200份订单的配货，由于订单量大幅增加，导致订单积 压．为解决困难，许多志愿者踊跃报名参加配货工作．已知该超市 某日积压500份订单未配货，预计第二天的新订单超过1600份的概 率为0.05，志愿者每人每天能完成50份订单的配货，为使第二天完 成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿 者() A.10名 B.18名 C.24名 D.32名 5.己知单位向量푎→，푏 → 的夹角为60∘，则下列向量中，与푏 → 垂直的 是() A.푎→ + 2푏 → B.2푎→ + 푏 → C.푎→ − 2푏 → D.2푎→ − 푏 → 6.记푆푛为等比数列{푎푛}的前푛项和．若푎5 − 푎3 = 12，푎6 − 푎4 = 24，则푆푛 푎푛 =() A.2푛 − 1 B.2 − 21−푛 C.2 − 2푛−1 D.21−푛 − 1 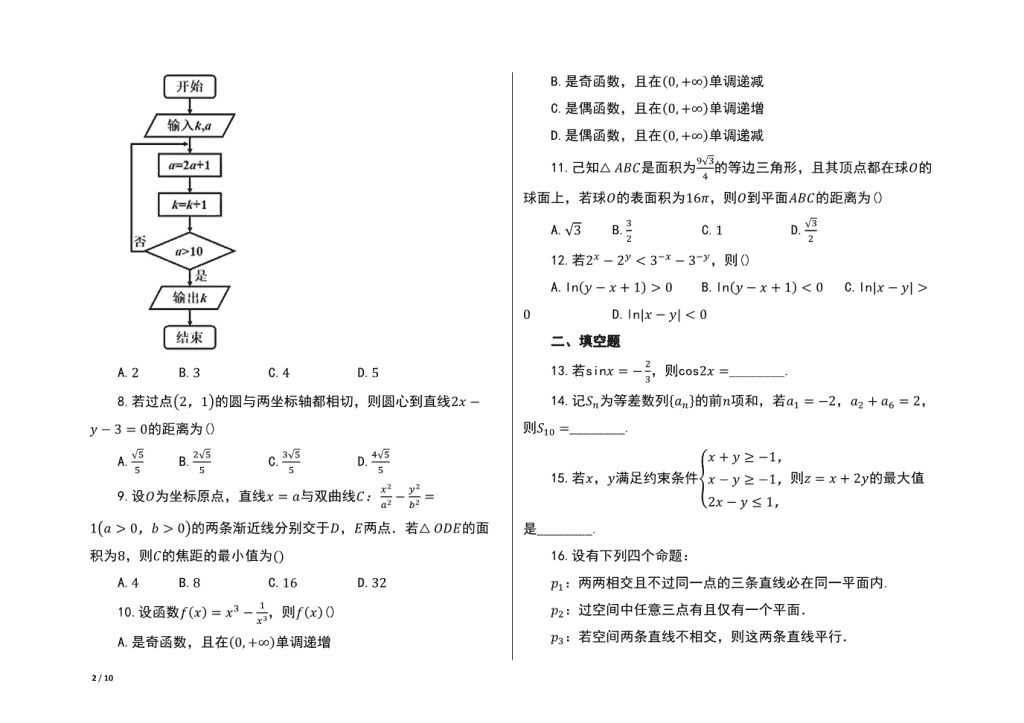7.执行下面的程序框图，若输入푘 = 0，푎 = 0，则输出的푘为() 2 / 10 A.2 B.3 C.4 D.5 8.若过点(2，1)的圆与两坐标轴都相切，则圆心到直线2푥 − 푦 − 3 = 0的距离为() A.√5 5 B.2√5 5 C.3√5 5 D.4√5 5 9.设푂为坐标原点，直线푥 = 푎与双曲线퐶： 푥2 푎2 − 푦2 푏2 = 1(푎 > 0，푏 > 0)的两条渐近线分别交于퐷，퐸两点．若△ 푂퐷퐸的面 积为8，则퐶的焦距的最小值为() A.4 B.8 C.16 D.32 10.设函数푓(푥) = 푥3 − 1 푥3，则푓(푥)() A.是奇函数，且在(0, +∞)单调递增 B.是奇函数，且在(0, +∞)单调递减 C.是偶函数，且在(0, +∞)单调递增 D.是偶函数，且在(0, +∞)单调递减 11.己知△ 퐴퐵퐶是面积为9√3 4 的等边三角形，且其顶点都在球푂的 球面上，若球푂的表面积为16휋，则푂到平面퐴퐵퐶的距离为() A.√3 B.3 2 C.1 D.√3 2 12.若2푥 − 2푦 < 3−푥 − 3−푦，则() A.ln(푦 − 푥 + 1) > 0 B.ln(푦 − 푥 + 1) < 0 C.ln|푥 − 푦| > 0 D.ln|푥 − 푦| < 0 二、填空题 13.若sin푥 = − 2 3 ，则cos2푥 =________. 14.记푆푛为等差数列{푎푛}的前푛项和，若푎1 = −2，푎2 + 푎6 = 2， 则푆10 =________. 15.若푥，푦满足约束条件{ 푥 + 푦 ≥ −1， 푥 − 푦 ≥ −1， 2푥 − 푦 ≤ 1， 则푧 = 푥 + 2푦的最大值 是________. 16.设有下列四个命题： 푝1：两两相交且不过同一点的三条直线必在同一平面内. 푝2：过空间中任意三点有且仅有一个平面． 푝3：若空间两条直线不相交，则这两条直线平行． 3 / 10 푝4：若直线푙 ⊂平面훼，直线푚 ⊥平面훼，则푚 ⊥ 푙. 则下述命题中所有真命题的序号是________. ①푝1 ∧ 푝4；②푝1 ∧ 푝2；③¬푝2 ∨ 푝3；④¬푝3 ∧ ¬푝4. 三、解答题 17.△ 퐴퐵퐶的内角퐴，퐵，퐶的对边分别为푎，푏，푐，己知 cos2 (휋 2 + 퐴) + cos퐴 = 5 4 . (1)求퐴； (2)푏 − 푐 = √3 3 푎，证明：△ 퐴퐵퐶是直角三角形． 18.某沙漠地区经过治理，生态系统得到很大改善，野生动物数 量有所增加．为调查该地区某种野生动物的数量，将其分成面积相 近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作 为样区，调查得到样本数据(푥1, 푦1)(푖 = 1,2, ⋯ ,20)，其中푥푖和푦푖分别 表示第푖个样区的植物覆盖面积（单位：公顷）和这种野生动物的数 量，并计算得∑ 푥푖 20 푖=1 = 60，∑ 푦푖 20 푖=1 = 1200，∑ (푥푖 − 푥¯ ) 220 푖=1 = 80， ∑ (푦푖 − 푦¯ ) 220 푖=1 = 9000，∑ (푥푖 − 푥¯ )20 푖=1 (푦푖 − 푦¯ ) = 800. (1)求该地区这种野生动物数量的估计值（这种野生动物数量的 估计值等于样区这种野生动物数量的平均数乘以地块数）； (2)求样本(푥푖, 푦푖)(푖 = 1,2, ⋯ ,20)的相关系数（精确到0.01）； (3)根据现有统计资料，各地块间植物覆盖面积差异很大．为提 高样本的代表性以获得该地区这种野生动物数量更准确的估计，请 给出一种你认为更合理的抽样方法，并说明理由． 附：相关系数푟 = ∑ (푥푖−푥¯ )푛 푖=1 (푦푖−푦¯ ) √∑ (푥푖−푥¯ ) 2푛 푖=1 ∑ (푦푖−푦¯ ) 2푛 푖=1 ，√2 ≈ 1.414. 4 / 10 19.已知椭圆퐶1: 푥2 푎2 + 푦2 푏2 = 1(푎 > 푏 > 0)的右焦点퐹与抛物线퐶2的 焦点重合，퐶1的中心与퐶2的顶点重合，过퐹且与푥轴垂直的直线交퐶1 于퐴，퐵两点，交퐶2于퐶，퐷两点，且|퐶퐷| = 4 3 |퐴퐵|. (1)求퐶1的离心率； (2)若퐶1的四个顶点到퐶2的准线距离之和为12，求퐶1与퐶2的标准 方程． 20.如图，已知三棱柱퐴퐵퐶 − 퐴1퐵1퐶1的底面是正三角形，侧面 퐵퐵1퐶1퐶是矩形，푀，푁分别为퐵퐶，퐵1퐶1的中点，푃为퐴푀上一点，过 퐵1퐶1和푃的平面交퐴퐵于퐸，交퐴퐶于퐹. 5 / 10 (1)证明：퐴퐴1//푀푁，且平面퐴1퐴푀푁 ⊥平面퐸퐵1퐶1퐹； (2)设푂为△ 퐴1퐵1퐶1的中心，若퐴푂 = 퐴퐵 = 6，퐴푂//平面 퐸퐵1퐶1퐹，且∠푀푃푁 = 휋 3 ，求四棱锥퐵 − 퐸퐵1퐶1퐹的体积． 21.已知函数푓(푥) = 2ln푥 + 1. (1)若푓(푥) ≤ 2푥 + 푐，求푐的取值范围； (2)设푎 > 0，讨论函数푔(푥) = 푓(푥)−푓(푎) 푥−푎 的单调性． 6 / 10 22.已知퐶1，퐶2的参数方程分别为퐶1： {푥 = 4cos2휃, 푦 = 4sin2휃（휃为参数）， 퐶2： { 푥 = 푡 + 1 푡 , 푦 = 푡 − 1 푡 （푡为参数）． (1)将퐶1，퐶2的参数方程化为普通方程； (2)以坐标原点为极点，正轴正半轴为极轴建立极坐标系，设퐶1， 퐶2的交点为푃，求圆心在极轴上，且经过极点和푃的圆的极坐标方程． 7 / 10 参考答案与试题解析 2020 年全国统一高考数学试卷（文科）（新课标Ⅱ） 一、选择题 1.D 2.A 3.C 4.B 5.D 6.B 7.C 8.B 9.B 10.A 11.C 12.A 二、填空题 13.1 9 14.25 15.8 16.①③④ 三、解答题 17.解：(1)由cos2 (휋 2 + 퐴) + cos퐴 = 5 4 可得：sin2퐴 + cos퐴 = 5 4 ， 4cos2퐴 − 4cos퐴 + 1 = 0， ⇒ (2cos퐴 − 1)2 = 0， ⇒ cos퐴 = 1 2 . ∵퐴 ∈ (0, 휋)， ∴퐴 = 휋 3 . (2)由푏 − 푐 = √3 3 푎可得푎 = √3(푏 − 푐)， 又cos퐴 = 푏2+푐2−푎2 2푏푐 = 1 2 ，即푏2 + 푐2 − 푎2 = 푏푐， 푏2 + 푐2 − 3(푏 − 푐)2 = 푏푐 ⇒ (푏 − 2푐)(2푏 − 푐) = 0， ∴푏 = 2푐或푐 = 2푏（舍）， ∴푎 = √3푐， 即푎2 + 푐2 = 푏2. 故三角形为直角三角形． 18.解：(1)野生动物数量的估计值为1200 ÷ 20 × 200 = 12000； (2)将数据代入公式得푟 = 800 √80×9000 = 800 600√2 = 2√2 3 ≈ 0.94； (3)应使用分层抽样． 因为各地块间植物覆盖面积差异很大，为提高样本的代表性应 从植物覆盖面积不同的各地块间进行抽取 8 / 10 19.解：(1)由题意知： { 2푝 = 4 3 ⋅ 2푏2 푎 , 푐 = 푝 2 , 푎2 = 푏2 + 푐2, ∴4푐 = 4 3 ⋅ 2푏2 푎 ， ∴3푎푐 = 2(푎2 − 푐2)，即2푐2 + 3푎푐 − 2푎2 = 0， ∴2푒2 + 3푒 − 2 = 0， ∴푒 = 1 2 或푒 = −2． ∵0 < 푒 < 1， ∴퐶1的离心率为1 2 . (2)设퐶1的四个顶点到퐶2的准线距离为푑1，푑2，푑3，푑4， 则： { 푑1 = 푎 − 푐, 푑2 = 푎 + 푐, 푑3 = 푐 = 푝 2 , 푑4 = 푐 = 푃 2 . 又∵푑1 + 푑2 + 푑3 + 푑4 = 12， ∴{ 푎 − 푐 + 푎 + 푐 + 푐 + 푐 = 12, 푐 = 푝 2 , ∴푎 + 푐 = 6． ∵푐 푎 = 1 2 ， ∴2푐 + 푐 = 6， ∴푎2 = 16，푐2 = 4，푝 = 2푐 = 4， ∴푏2 = 12， ∴퐶1： 푥2 16 + 푦2 12 = 1，퐶2：푦2 = 8푥. 20.(1)证明：由题意知퐴퐴1//퐵퐵1//퐶퐶1. 又因为侧面퐵퐵1퐶1퐶是矩形，且푀，푁分别是퐵퐶，퐵1퐶1的中点， 所以푀푁//퐵퐵1，퐵퐵1 ⊥ 퐵퐶， 所以퐴퐴1//푀푁，푀푁 ⊥ 퐵1퐶1. 又因为底面是正三角形， 所以퐴푀 ⊥ 퐵퐶，퐴푁 ⊥ 퐵1퐶1. 又因为푀푁 ∩ 퐴푀 = 푀， 所以퐵1퐶1 ⊥平面퐴1퐴푀푁. 又因为平面퐸퐵1퐶1퐹 ∩平面퐴1퐵1퐶1 = 퐵1퐶1，平面퐸퐵1퐶1퐹 ∩平面 퐴퐵퐶 = 퐸퐹，平面퐴퐵퐶//平面퐴1퐵1퐶1， 所以퐸퐹//퐵1퐶1， 所以퐸퐹 ⊥平面퐴1퐴푀푁. 又因为퐸퐹 ⊂平面퐸퐵1퐶1퐹， 所以平面퐴1퐴푀푁 ⊥平面퐸퐵1퐶1퐹. (2)解：因为퐴푂//平面퐸퐵1퐶1퐹，퐴푂 ⊂平面퐴1푁푀퐴， 平面퐴1푁푀퐴 ∩平面퐸퐵1퐶1퐹 = 푁푃， 所以퐴푂//푁푃. 又因为푁푂//퐴푃， 所以四边形퐴푃푁푂是平行四边形， 9 / 10 所以퐴푂 = 푁푃 = 6，푂푁 = 퐴푃 = √3. 过푀做푀퐻垂直푁푃于퐻. 因为平面퐸퐵1퐶1퐹 ⊥平面퐴1퐴푀푁，平面퐸퐵1퐶1퐹 ∩平面퐴1퐴푀푁 = 푁푃，푀퐻 ⊂平面퐴1퐴푀푁， 所以푀퐻 ⊥平面퐸퐵1퐶1퐹. 因为∠푀푃푁 = 휋 3 ， 所以푀퐻 = 푀푃 ⋅ sin 휋 3 = 3，푆퐸퐵1퐶1퐹 = 1 2 (퐵1퐶1 + 퐸퐹) ⋅ 푁푃 = 24. 因为퐵퐶//平面퐸퐵1퐶1퐹， 所以푉퐵−퐸퐵1퐶1퐹 = 푉푀−퐸퐵1퐶1퐹 = 1 3 ⋅ 푆퐸퐵1퐶1퐹 ⋅ 푀퐻 = 24. 21.解：(1)푓(푥) ≤ 2푥 + 푐等价于2ln푥 − 2푥 ≤ 푐 − 1， 设ℎ(푥) = 2ln푥 − 2푥，则ℎ′(푥) = 2 푥 − 2 = 2(1−푥) 푥 ， 所以ℎ(푥)在(0，1)上单调递增，在(1， + ∞)上单调递减， 所以ℎ(푥)max = ℎ(1) = −2. 所以푐 − 1 ≥ −2，即푐 ≥ −1， 所以푐的取值范围是[−1, +∞). (2)푔(푥) = 2(ln푥−ln푎) 푥−푎 (푥 > 0，푥 ≠ 푎，푎 > 0)， 所以푔′(푥) = 2 푥(푥−푎)−2ln푥+2ln푎 (푥−푎)2 = −2푎 푥 −2ln푥+2ln푎+2 (푥−푎)2 . 令푤(푥) = − 2푎 푥 − 2ln푥 + 2ln푎 + 2(푥 > 0)， 则푤′(푥) = 2푎 푥2 − 2 푥 = 2(푎−푥) 푥2 . 令푤′(푥) > 0，得0 < 푥 < 푎， 所以，푤(푥)在(0，푎)上单调递增，在(푎， + ∞)上递减， 所以，푤(푥) ≤ 푤(푎) = 0，即푔′(푥) ≤ 0， 所以，푔(푥)在(0，푎)和(푎， + ∞)上单调递减． 22.解：(1)由题：퐶1的普通方程为：푥 + 푦 − 4 = 0, (푥 ≥ 0, 푦 > 0)； 因为퐶2： { 푥2 = 푡2 + 1 푡2 + 2, 푦2 = 푡2 + 1 푡2 − 2, ， 故퐶2的普通方程为：푥2 − 푦2 = 4. (2)联立퐶1，퐶2，{푥 + 푦 − 4 = 0, 푥2 − 푦2 = 4, 解得：{ 푥 = 5 2 , 푦 = 3 2 , 所以点푃坐标为：푃 (5 2 , 3 2). 10 / 10 设所求圆圆心为푄(푎, 0)，半径为푎， 故圆心푄(푎, 0)到푃 (5 2 , 3 2)的距离为 √(5 2 − 푎) 2 + (3 2 − 0) 2 = 푎，解得푎 = 17 10 ， 所以圆푄的圆心为푄 (17 10 , 0)，半径为17 10 ， 圆푄的直角坐标方程为：(푥 − 17 10) 2 = (17 10) 2 ， 将方程化为一般形式为：푥2 − 17 5 푥 + 푦2 = 0， 化为极坐标方程为：휌2 = 17 5 cos휃.