函数y=Asin（ωx+ψ）教案2 6页

‎ ‎ ‎ 函数y＝Asin(ωx＋)的图象教案 ‎●教学目标 ‎(一)知识目标 ‎1.相位变换中的有关概念； 2.y＝sin(x＋)的图象的画法.‎ ‎(二)能力目标 ‎1.理解相位变换中的有关概念；‎ ‎2.会用相位变换画出函数的图象；‎ ‎3.会用“五点法”画出y＝sin(x＋)的简图.‎ ‎(三)德育目标 ‎1.数形结合思想的渗透；‎ ‎2.辩证观点的培养；‎ ‎3.数学修养的培养.‎ ‎●教学重点 ‎1.相位变换中的有关概念；‎ ‎2.会用相位变换画函数图象；‎ ‎3.“五点法”画y＝sin(x＋)的简图.‎ ‎●教学难点 理解并利用相位变换画图象.‎ ‎●教学方法 引导学生体会作图过程从而理解相位变换.(讲练结合法)‎ ‎●教学过程 Ⅰ.课题导入 师：我们随着学习三角函数的深入，还会遇到形如y＝sin(x＋)的三角函数，这种函数的图象又该如何得到呢?今天，我们一起来探讨一下.‎ Ⅱ.讲授新课 师：下面看例子 ‎［例］画出函数 y＝sin(x＋)，x∈R y＝sin(x－)，x∈R 的简图.‎ 解：列表 x ‎-‎ X=x+‎ ‎0‎ ‎2‎ 6‎ ‎ ‎ sin(x+)‎ ‎0‎ ‎1‎ ‎0‎ ‎–1‎ ‎0‎ 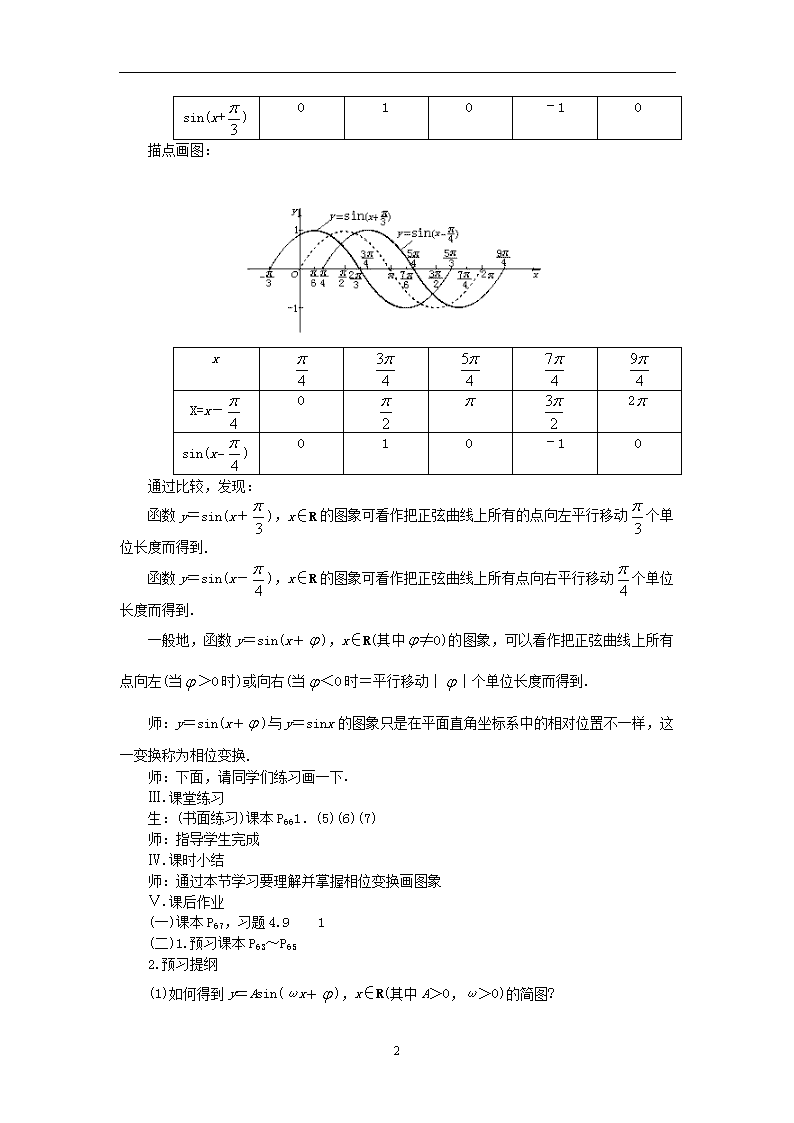描点画图：‎ x X=x－‎ ‎0‎ ‎2‎ sin(x–)‎ ‎0‎ ‎1‎ ‎0‎ ‎–1‎ ‎0‎ 通过比较，发现：‎ 函数y＝sin(x＋)，x∈R的图象可看作把正弦曲线上所有的点向左平行移动个单位长度而得到.‎ 函数y＝sin(x－)，x∈R的图象可看作把正弦曲线上所有点向右平行移动个单位长度而得到.‎ 一般地，函数y＝sin(x＋)，x∈R(其中≠0)的图象，可以看作把正弦曲线上所有点向左(当＞0时)或向右(当＜0时＝平行移动｜｜个单位长度而得到.‎ 师：y＝sin(x＋)与y＝sinx的图象只是在平面直角坐标系中的相对位置不一样，这一变换称为相位变换.‎ 师：下面，请同学们练习画一下.‎ Ⅲ.课堂练习 生：(书面练习)课本P661．(5)(6)(7)‎ 师：指导学生完成 Ⅳ.课时小结 师：通过本节学习要理解并掌握相位变换画图象 Ⅴ.课后作业 ‎(一)课本P67，习题4.9 1‎ ‎(二)1.预习课本P63～P65‎ ‎2.预习提纲 ‎(1)如何得到y＝Asin(ωx＋)，x∈R(其中A＞0，ω＞0)的简图?‎ 6‎ ‎ ‎ ‎(2)作图步骤为何?‎ ‎(3)多种变换的顺序又如何?‎ ‎●板书设计 课题 课时小结 例 ‎●备课资料 ‎1.(1)y＝sin(x＋)是由y＝sinx向左平移个单位得到的.‎ ‎(2)y＝sin(x－)是由y＝sinx向右平移个单位得到的.‎ ‎(3)y＝sin(x－)是由y＝sin(x＋)向右平移个单位得到的.‎ ‎2.若将某函数的图象向右平移以后所得到的图象的函数式是y＝sin(x＋)，则原来的函数表达式为( )‎ A.y＝sin(x＋) B.y＝sin(x＋)‎ C.y＝sin(x－) D.y＝sin(x＋)－‎ 答案：A ‎3.把函数y＝cos(3x＋)的图象适当变动就可以得到y＝sin(－3x)的图象，这种变动可以是( )‎ A.向右平移 B.向左平移 C.向右平移 D.向左平移 分析：三角函数图象变换问题的常规题型是：已知函数和变换方法，求变换后的函数或图象，此题是已知变换前后的函数，求变换方式的逆向型题目，解题的思路是将异名函数化为同名函数，且须x的系数相同.‎ 解：∵y＝cos(3x＋)＝sin(－3x)＝sin［－3(x－)］‎ ‎∴由y＝sin［－3(x-)］向左平移才能得到y＝sin(－3x)的图象.‎ 答案：D ‎4.将函数y＝f(x)的图象沿x轴向右平移，再保持图象上的纵坐标不变，而横坐标变为原来的2倍，得到的曲线与y＝sinx的图象相同，则y＝f(x)是( )‎ A.y＝sin(2x＋) B.y＝sin(2x－)‎ 6‎ ‎ ‎ C.y＝sin(2x＋) D.y＝sin(2x－)‎ 分析：这是三角图象变换问题的又一类逆向型题，解题的思路是逆推法.‎ 解：y＝f(x)可由y＝sinx，纵坐标不变，横坐标压缩为原来的1/2，得y=sin2x;再沿x轴向左平移得y＝sin2(x＋)，即f(x)＝sin(2x＋).‎ 答案：C ‎5.若函数f(x)＝sin2x＋acos2x的图象关于直线x＝－对称，则a＝–1.‎ 分析：这是已知函数图象的对称轴方程，求函数解析式中参数值的一类逆向型题，解题的关键是如何巧用对称性.‎ 解：∵x1＝0，x2＝－是定义域中关于x＝－对称的两点 ‎∴f(0)＝f(－)‎ 即0＋a＝sin(－)＋acos(－)‎ ‎∴a＝－1‎ ‎6.若对任意实数a，函数y＝5sin(πx－)(k∈Ｎ)在区间［a，a＋3］上的值出现不少于4次且不多于8次，则k的值是( )‎ A.2 B.4 C.3或4 D.2或3‎ 分析：这也是求函数解析式中参数值的逆向型题，解题的思路是：先求出与k相关的周期T的取值范围，再求k.‎ 解：∵T＝‎ 又因每一周期内出现值时有2次，出现4次取2个周期，出现值8次应有4个周期.‎ ‎∴有4T≥3且2T≤3‎ 即得≤T≤，∴≤≤‎ 解得≤k≤，∵k∈Ｎ，∴k＝2或3.‎ 答案：D 附：巧求初相角 求初相角是高中数学学习中的一个难点，怎样求初相角?初相角有几个?下面通过错解剖析，介绍四种方法.‎ 如图，它是函数y＝Asin(ωx＋)(A＞0，ω＞0)，｜｜＜π的图象，‎ 由图中条件，写出该函数解析式.‎ 6‎ ‎ ‎ 错解：‎ 由图知：A＝5‎ 由 得T＝3π，∴ω＝＝‎ ‎∴y＝5sin(x＋)‎ 将(π，0)代入该式得：5sin(π＋)＝0‎ 由sin(＋)＝0，得＋＝kπ ‎＝kπ－ (k∈Z)‎ ‎∵｜｜＜π，∴＝－或＝‎ ‎∴y＝5sin(x－)或y＝5sin(x＋)‎ 分析：由题意可知，点(，5)在此函数的图象上，但在y＝5sin(x－)中，令x＝，则y＝5sin(－)＝5sin(－)＝－5，由此可知：y＝5sin(x－)不合题意.‎ 那么，问题出在哪里呢?我们知道，已知三角函数值求角，在一个周期内一般总有两个解，只有在限定的范围内才能得出惟一解.‎ 正解一：(单调性法)‎ ‎∵点(π，0)在递减的那段曲线上 ‎∴＋∈［＋2kπ，＋2kπ］(k∈Z)‎ 由sin(＋)＝0得＋＝2kπ＋π ‎∴＝2kπ＋ (k∈Z)‎ ‎∵｜｜＜π，∴＝‎ 正解二：(最值点法)‎ 将最高点坐标(，5)代入y＝5sin(x＋)得5sin(＋)＝5‎ ‎∴＋＝2kπ＋‎ ‎∴＝2kπ＋ (k∈Z)取＝‎ 正解三：(起始点法)‎ 函数y＝Asin(ωx＋)的图象一般由“五点法”作出，而起始点的横坐标x正是由ωx+‎ 6‎ ‎ ‎ ‎=0解得的，故只要找出起始点横坐标x0,就可以迅速求得角.由图象求得x0=-,∴=-ωx0=- (-)=.‎ 正解四：(平移法)‎ 由图象知，将y=5sin(x)的图象沿x轴向左平移个单位，就得到本题图象，故所求函数为y＝5sin(x＋)，即y＝5sin(x＋).‎ ‎●教学后记 6‎