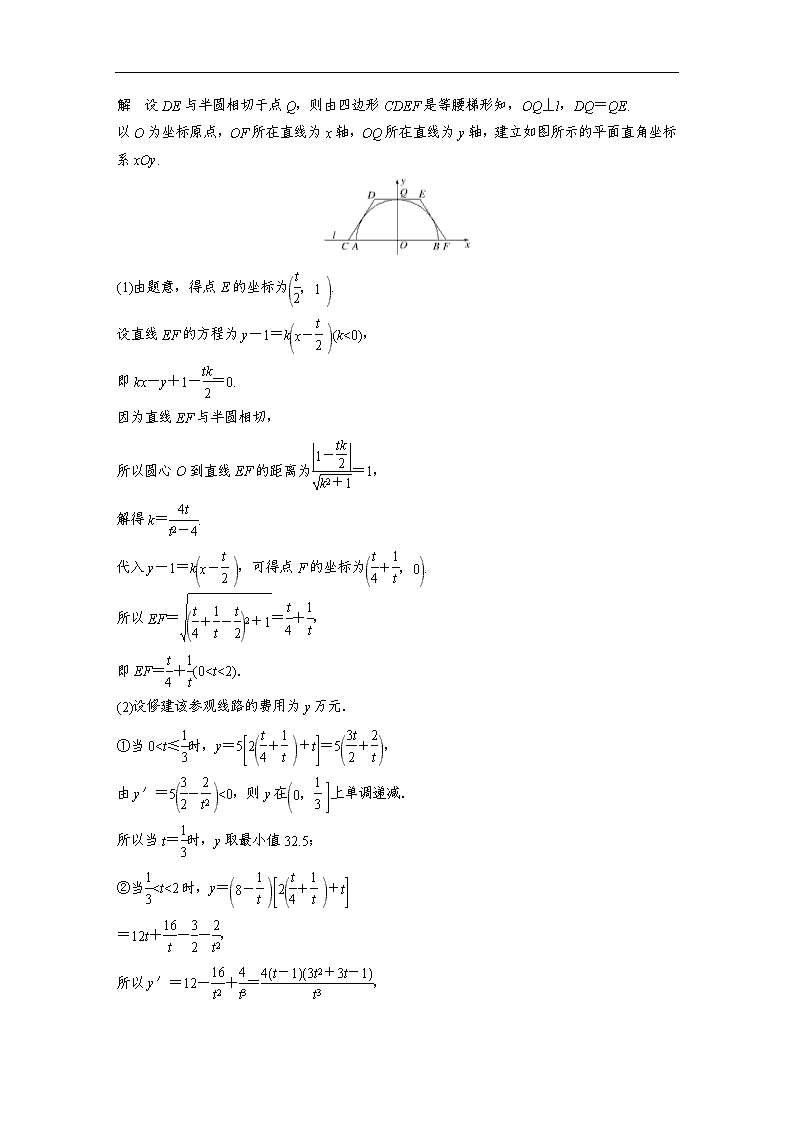2019年高考数学练习题汇总高考解答题仿真练1 8页

高考解答题仿真练1‎ ‎1．已知向量m＝(cos x,1)，n＝，f(x)＝m·n.‎ ‎(1)求f(x)在[0，π]上的单调递增区间；‎ ‎(2)在△ABC中，若角A，B，C的对边分别是a，b，c，且f(B)＝，sin Asin C＝sin2B，求a－c的值．‎ 解　由题意得，f(x)＝cos xsin＋1‎ ‎＝cos x＋1‎ ‎＝sin 2x－×＋1‎ ‎＝sin 2x－cos 2x＋ ‎＝sin＋.‎ ‎(1)由2kπ－≤2x－≤2kπ＋，k∈Z，‎ 得kπ－≤x≤kπ＋，k∈Z，‎ 又x∈[0，π]，‎ ‎∴f(x)在[0，π]上的单调递增区间是和.‎ ‎(2)由f(B)＝sin＋＝，‎ 得sin＝1.‎ 又B是△ABC的内角，∴2B－＝，B＝.‎ 又sin Asin C＝sin2B，∴由正弦定理可得ac＝b2.‎ 在△ABC中，由余弦定理b2＝a2＋c2－2accos B，‎ 可得ac＝(a－c)2＋2ac－ac，则a－c＝0.‎ ‎2.如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，平面ABP⊥平面BCP，∠APB＝90°，BP＝BC，M为PC的中点．求证：‎ ‎(1)AP∥平面BDM；‎ ‎(2)BM⊥平面ACP.‎ 证明　(1)设AC∩BD＝O，连结OM，‎ 因为ABCD是平行四边形，‎ 所以O为AC的中点．‎ 因为M为PC的中点，所以AP∥OM.‎ 又因为AP⊄平面BDM，OM⊂平面BDM，‎ 所以AP∥平面BDM.‎ ‎(2)因为∠APB＝90°，所以AP⊥BP.‎ 又因为平面ABP⊥平面BCP，平面ABP∩平面BCP＝BP，AP⊂平面ABP，‎ 所以AP⊥平面BCP.‎ 又因为BM⊂平面BCP，所以AP⊥BM.‎ 因为BP＝BC，M为PC的中点，所以BM⊥CP.‎ 又因为AP∩CP＝P，AP，CP⊂平面ACP，‎ 所以BM⊥平面ACP.‎ ‎3．如图，半圆AOB是某爱国主义教育基地一景点的平面示意图，半径OA的长为1百米．为了保护景点，基地管理部门从道路l上选取一点C，修建参观线路C－D－E－F，且CD，DE，EF均与半圆相切，四边形CDEF是等腰梯形．设DE＝t百米，记修建每1百米参观线路的费用为f(t)万元，经测算f(t)＝ ‎(1)用t表示线段EF的长；‎ ‎(2)求修建该参观线路的最低费用．‎ 解　设DE与半圆相切于点Q，则由四边形CDEF是等腰梯形知，OQ⊥l，DQ＝QE.‎ 以O为坐标原点，OF所在直线为x轴，OQ所在直线为y轴，建立如图所示的平面直角坐标系xOy.‎ ‎(1)由题意，得点E的坐标为.‎ 设直线EF的方程为y－1＝k(k<0)，‎ 即kx－y＋1－＝0.‎ 因为直线EF与半圆相切，‎ 所以圆心O到直线EF的距离为＝1，‎ 解得k＝. ‎ 代入y－1＝k，可得点F的坐标为.‎ 所以EF＝＝＋，‎ 即EF＝＋(00，‎ 所以当t∈时，y′<0，当t∈(1,2)时，y′>0，‎ 所以y在上单调递减；在(1,2)上单调递增．‎ 所以当t＝1时，y取最小值24.5.‎ 由①②知，修建该参观线路的最低费用为24.5 万元．‎ ‎4．(2018·江苏金陵中学调研)如图，在平面直角坐标系xOy中，已知椭圆＋＝1(a>b>0)的离心率为，且过点.设F为椭圆的右焦点，A，B为椭圆上关于原点对称的两点，连结AF，BF并延长，分别交椭圆于C，D两点．‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设直线AB，CD的斜率分别为k1，k2，是否存在实数m，使得k2＝mk1？若存在，求出实数m的值；若不存在，请说明理由．‎ 解　(1)设椭圆的半焦距为c，‎ 则c＝，‎ 由题意知 解得所以椭圆的标准方程为＋y2＝1.‎ ‎(2)①当AF⊥x轴时，A，B，‎ C，F(，0)．‎ 则kBF＝，直线BD的方程为y＝(x－)．‎ 由消去y，‎ 得13x2－2x－45＝0，‎ 因为x＝－是该方程的一个解，‎ 所以点D的横坐标xD＝，‎ 则yD＝，即D.‎ 所以k2＝＝，‎ 又k1＝，所以k2＝7k1，即m＝7.‎ ‎②当AF与x轴不垂直时，‎ 设A(x0，y0)，则B(－x0，－y0)，k1＝，‎ 又F(，0)，‎ 所以直线AF的方程为y＝(x－)．‎ 由消去y，‎ 得(7－2x0)x2－8yx －7x＋8x0＝0.‎ 因为x＝x0是该方程的一个解，‎ 所以点C的横坐标xC＝.‎ 又点C(xC，yC)在直线y＝(x－)上，‎ 所以yC＝(xC－)＝，‎ 从而点C的坐标为，‎ 同理，点D的坐标为，‎ 所以k2＝ ＝＝7k1，即m＝7.‎ 综合①②可知，存在m＝7，使得k2＝7k1.‎ ‎5．已知函数f(x)＝xln x，g(x)＝λ(x2－1)(λ为常数)．‎ ‎(1)若函数y＝f(x)与函数y＝g(x)在x＝1处有相同的切线，求实数λ的值；‎ ‎(2)若λ＝，且x≥1，证明：f(x)≤g(x)；‎ ‎(3)若对任意x∈[1，＋∞)，不等式f(x)≤g(x)恒成立，求实数λ的取值范围．‎ ‎(1)解　f′(x)＝ln x＋1，则f′(1)＝1且f(1)＝0，‎ 所以函数y＝f(x)在x＝1处的切线方程为y＝x－1，‎ 从而g′(1)＝2λ＝1，即λ＝.‎ ‎(2)证明　设函数h(x)＝xln x－(x2－1)，x∈[1，＋∞)，‎ 则h′(x)＝ln x＋1－x.‎ 设p(x)＝ln x＋1－x，从而p′(x)＝－1≤0对任意x∈[1，＋∞)恒成立，‎ 所以p(x)＝ln x＋1－x≤p(1)＝0，即h′(x)≤0，‎ 因此函数h(x)＝xln x－(x2－1)在[1，＋∞)上单调递减，‎ 即h(x)≤h(1)＝0，所以当x≥1时，f(x)≤g(x)成立．‎ ‎(3)解　设函数H(x)＝xln x－λ(x2－1)，x∈[1，＋∞)，‎ 从而对任意x∈[1，＋∞)，不等式H(x)≤0＝H(1)恒成立．‎ 又H′(x)＝ln x＋1－2λx，‎ 当H′(x)＝ln x＋1－2λx≤0，即≤2λ恒成立时，函数H(x)单调递减．‎ 设r(x)＝，x∈[1，＋∞)，‎ 则r′(x)＝≤0，‎ 所以r(x)max＝r(1)＝1，即2λ≥1，‎ 所以λ≥，符合题意；‎ 当λ≤0时，H′(x)＝ln x＋1－2λx≥0恒成立，此时函数H(x)单调递增．‎ 于是，不等式H(x)≥H(1)＝0对任意x∈[1，＋∞)恒成立，不符合题意；‎ 当0<λ<时，设q(x)＝H′(x)＝ln x＋1－2λx，x≥1，‎ 则由q′(x)＝－2λ＝0，得x＝>1.‎ 当x∈时，q′(x)＝－2λ>0，‎ 此时q(x)＝H′(x)＝ln x＋1－2λx单调递增，‎ 所以H′(x)＝ln x＋1－2λx>H′(1)＝1－2λ>0，‎ 故当x∈时，函数H(x)单调递增．‎ 于是当x∈时，H(x)>0成立，不符合题意．‎ 综上所述，实数λ的取值范围为.‎ ‎6．(2018·苏州调研)已知等差数列{an}的前2m－1项中，奇数项的和为56，偶数项的和为48，且a2＝3(其中m∈N*)．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)若ak1，ak2，…，akn，…是一个等比数列，其中k1＝1，k2＝5，求数列{kn}的通项公式；‎ ‎(3)若存在实数a，b，使得a≤≤b对任意n∈N*恒成立，求b－a的最小值．‎ 解　(1)由题意，·m＝56，‎ ·(m－1)＝48，‎ 因为a2＋a2m－2＝a1＋a2m－1，‎ 所以＝，解得m＝7.‎ 所以a1＋a13＝16，‎ 因为a1＋a13＝a2＋a12，且a2＝3，‎ 所以a12＝13.‎ 设数列{an}的公差为d，则10d＝a12－a2＝10，‎ 所以d＝1.‎ 所以a1＝2，通项公式an＝n＋1(n∈N*)．‎ ‎(2)由题意，ak1＝a1＝2，ak2＝a5＝6，‎ 设这个等比数列的公比为q，则q＝＝3.‎ 那么akn＝2×3n－1，‎ 另一方面akn＝kn＋1，所以kn＝2×3n－1－1(n∈N*)．‎ ‎(3)记cn＝＝，‎ 则cn＋1－cn＝－ ＝.‎ 因为n∈N*，‎ 所以当n≥2时，－2n2＋2n＋3＝－2n(n－1)＋3<0，‎ 即cn＋10，‎ 所以当n＝2时，cn取最大值c2＝，‎ 所以b≥.‎ 又c1＝0，当n>1时，cn>0，‎ 所以当n＝1时，cn取最小值c1＝0，所以a≤0.‎ 综上，b－a的最小值为.‎