2020版高中数学 第2章 数列 第1课时 等比数列的前n项和 9页

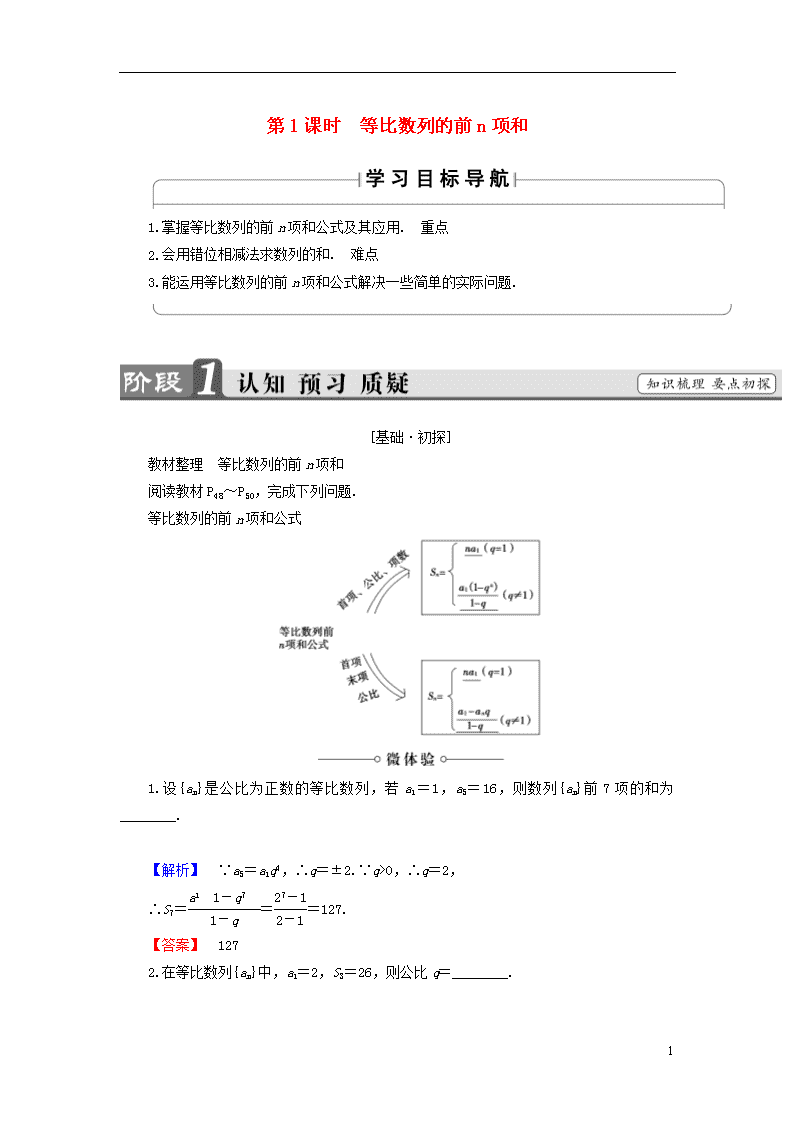
第1课时　等比数列的前n项和 ‎1.掌握等比数列的前n项和公式及其应用.(重点) ‎2.会用错位相减法求数列的和.(难点) ‎3.能运用等比数列的前n项和公式解决一些简单的实际问题.‎ ‎[基础·初探]‎ 教材整理　等比数列的前n项和 阅读教材P48～P50，完成下列问题.‎ 等比数列的前n项和公式 ‎1.设{an}是公比为正数的等比数列，若a1＝1，a5＝16，则数列{an}前7项的和为________.‎ ‎【解析】　∵a5＝a1q4，∴q＝±2.∵q>0，∴q＝2，‎ ‎∴S7＝＝＝127.‎ ‎【答案】　127‎ ‎2.在等比数列{an}中，a1＝2，S3＝26，则公比q＝________.‎ ‎【解析】　∵S3＝＝＝26，∴q2＋q－12＝0，∴q＝3或－4.‎ 9‎ ‎【答案】　3或－4‎ ‎3.等比数列{an}中，公比q＝－2，S5＝44，则a1＝________.‎ ‎【解析】　由S5＝＝44，‎ 得a1＝4.‎ ‎【答案】　4‎ ‎4.设Sn为等比数列{an}的前n项和，‎8a2＋a5＝0，则＝________.‎ ‎【解析】　由‎8a2＋a5＝0，‎ 得＝－8，即q3＝－8，‎ 所以q＝－2.‎ ＝＝＝－11.‎ ‎【答案】　－11‎ ‎[小组合作型]‎ 等比数列的前n项和公式的基本运算 ‎　在等比数列{an}中，‎ ‎(1)若Sn＝189，q＝2，an＝96，求a1和n；‎ ‎(2)若a3＝，S3＝，求a1和公比q.‎ ‎【精彩点拨】　利用等比数列的前n项和公式及通项公式，列出方程组求相应各个量.‎ ‎【自主解答】　(1)法一：由Sn＝，an＝a1qn－1以及已知条件得 ‎∴a1·2n＝192，‎ ‎∴2n＝.‎ ‎∴189＝a1(2n－1)＝a1，‎ ‎∴a1＝3.‎ 9‎ 又∵2n－1＝＝32，∴n＝6.‎ 法二：由公式Sn＝及条件得 ‎189＝，解得a1＝3，‎ 又由an＝a1·qn－1，‎ 得96＝3·2n－1，解得n＝6.‎ ‎(2)①当q≠1时，S3＝＝，‎ 又a3＝a1·q2＝，‎ ‎∴a1(1＋q＋q2)＝，‎ 即(1＋q＋q2)＝，‎ 解得q＝－(q＝1舍去)，∴a1＝6.‎ ‎②当q＝1时，S3＝‎3a1，∴a1＝.‎ 综上得或 ‎1.在等比数列 {an}的五个量a1，q，an，n，Sn中，已知其中的三个量，通过列方程组求解，就能求出另外两个量，这是方程思想与整体思想在数列中的具体应用.‎ ‎2.在解决与前n项和有关的问题时，首先要对公比q＝1或q≠1进行判断，若两种情况都有可能，则要分类讨论.‎ ‎[再练一题]‎ ‎1.在等比数列{an}中，‎ ‎(1)若q＝2，S4＝1，求S8; ‎ ‎【导学号：18082035】‎ ‎(2)若a1＋a3＝10，a4＋a6＝，求a4和S5.‎ ‎【解】　(1)法一：设首项为a1，∵q＝2，‎ S4＝1，∴＝1，即a1＝，‎ 9‎ ‎∴S8＝＝＝17.‎ 法二：∵S4＝＝1，且q＝2，‎ ‎∴S8＝＝(1＋q4)＝S4·(1＋q4)＝1×(1＋24)＝17.‎ ‎(2)设公比为q，由通项公式及已知条件得 即 ‎∵a1≠0,1＋q2≠0，‎ ‎∴②÷①得，q3＝，即q＝，‎ ‎∴a1＝8.‎ ‎∴a4＝a1q3＝8×＝1，‎ S5＝＝＝.‎ 等比数列前n项和公式的实际应用 ‎　借贷10 000元，以月利率为1%，每月以复利计息借贷，王老师从借贷后第二个月开始等额还贷，分6个月付清，试问每月应支付多少元？(1.016≈1.061,1.015≈1.051)‎ ‎【精彩点拨】　解决等额还贷问题关键要明白以下两点 ‎(1)所谓复利计息，即把上期的本利和作为下一期本金，在计算时每一期本金的数额是不同的，复利的计算公式为S＝P(1＋r)n，其中P代表本金，n代表存期，r代表利率，S代表本利和.‎ ‎(2)从还贷之月起，每月还贷金额是构成等比数列还是等差数列，首项是什么，公比或公差是多少.‎ ‎【自主解答】　法一：设每个月还贷a元，第1个月后欠款为a0元，以后第n个月还贷a元后，还剩下欠款an元(1≤n≤6)，‎ 则a0＝10 000，a1＝‎1.01a0－a，‎ a2＝‎1.01a1－a＝‎1.012a0－(1＋1.01)a，‎ ‎…‎ a6＝‎1.01a5－a＝…＝‎1.016a0－[1＋1.01＋…＋1.015]a.‎ 由题意，可知a6＝0，‎ 9‎ 即‎1.016a0－[1＋1.01＋…＋1.015]a＝0，‎ a＝.‎ ‎∵1.016＝1.061，‎ ‎∴a＝≈1 739.‎ 故每月应支付1 739元.‎ 法二：一方面，借款10 000元，将此借款以相同的条件存储6个月，则它的本利和为 S1＝104(1＋0.01)6＝104×(1.01)6(元).‎ 另一方面，设每个月还贷a元，分6个月还清，到贷款还清时，其本利和为 S2＝a(1＋0.01)5＋a(1＋0.01)4＋…＋a ‎＝ ‎＝a[1.016－1]×102(元).‎ 由S1＝S2，得a＝.‎ 以下解法同法一，得a≈1 739，故每月应支付1 739元.‎ 解数列应用题的具体方法步骤：‎ (1)认真审题，准确理解题意，达到如下要求,①明确问题属于哪类应用问题，即明确是等差数列问题还是等比数列问题，还是含有递推关系的数列问题？是求an，还是求Sn？特别要注意准确弄清项数是多少.,②弄清题目中主要的已知事项.‎ (2)抓住数量关系，联想数学知识和数学方法，恰当引入参数变量，将文字语言翻译成数学语言，将数量关系用数学式子表达 (3)将实际问题抽象为数学问题，将已知与所求联系起来，列出满足题意的数学关系式.‎ ‎[再练一题]‎ ‎2.为保护我国的稀土资源，国家限定某矿区的出口总量不能超过80吨，该矿区计划从2014年开始出口，当年出口a吨，以后每年出口量均比上一年减少10%.‎ ‎(1)以2014年为第一年，设第n年出口量为an吨，试求an的表达式；‎ ‎(2)因稀土资源不能再生，国家计划10年后终止该矿区的出口，问2014年最多出口多少吨？(保留一位小数.参考数据：0.910≈0.35.)‎ ‎【解】　(1)由题意知每年的出口量构成等比数列，且首项a1＝a，公比q＝1－10%＝0.9，∴an＝a·0.9n－1(n≥1).‎ 9‎ ‎(2)10年的出口总量 S10＝＝‎10a(1－0.910).‎ ‎∵S10≤80，‎ ‎∴‎10a(1－0.910)≤80，即a ≤，‎ ‎∴a≤12.3，故2014年最多出口12.3吨.‎ ‎[探究共研型]‎ 错位相减法求和 探究1　由项数相等的等差数列{n}与等比数列{2n}相应项的积构成新的数列{n·2n}是等比数列吗？是等差数列吗？该数列的前n项和Sn的表达式是什么？‎ ‎【提示】　由等差数列及等比数列的定义可知数列{n·2n}既不是等差数列，也不是等比数列.该数列的前n项和Sn的表达式为Sn＝1·21＋2·22＋3·23＋…＋n·2n.‎ 探究2　在等式 Sn＝1·21＋2·22＋3·23＋…＋n·2n两边同乘以数列{2n}的公比后，该等式的变形形式是什么？认真观察两式的结构特征，你能将求Sn的问题转化为等比数列的前n项和问题吗？‎ ‎【提示】　在等式Sn＝1·21＋2·22＋3·23＋…＋n·2n ①‎ 两边同乘以{2n}的公比可变形为 ‎2Sn＝1·22＋2·23＋3·24＋…＋(n－1)·2n＋n·2n＋1 ②‎ ‎②－①得：Sn＝－1·21－22－23－24－…－2n＋n·2n＋1‎ ‎＝－(21＋22＋23＋…＋2n)＋n·2n＋1.‎ 此时可把求Sn的问题转化为求等比数列{2n}的前n项和问题.我们把这种求由一个等差数列{an}和一个等比数列{bn}相应项的积构成的数列{anbn}前n项和的方法叫错位相减法.‎ ‎　已知数列{an}的前n项和Sn＝3n2＋8n，{bn}是等差数列，且an＝bn＋bn＋1.‎ ‎(1)求数列{bn}的通项公式；‎ ‎(2)令cn＝，求数列{cn}的前n项和Tn.‎ ‎【精彩点拨】　(1)利用Sn与an的关系求出an，再利用待定系数法求出bn.(2)先化简cn，再利用错位相减法求和.‎ ‎【自主解答】　(1)由题意知，当n≥2时，an＝Sn－Sn－1＝6n＋5，‎ 当n＝1时，a1＝S1＝11，满足上式，‎ 所以an＝6n＋5.‎ 设数列{bn}的公差为d.‎ 由即 可解得所以bn＝3n＋1.‎ 9‎ ‎(2)由(1)知cn＝＝3(n＋1)·2n＋1，‎ 又Tn＝c1＋c2＋…＋cn，‎ 得Tn＝3×[2×22＋3×23＋…＋(n＋1)×2n＋1]，‎ ‎2Tn＝3×[2×23＋3×24＋…＋(n＋1)×2n＋2]，‎ 两式作差，得－Tn＝3×[2×22＋23＋24＋…＋2n＋1－(n＋1)×2n＋2]‎ ‎＝3× ‎＝－3n·2n＋2，‎ 所以Tn＝3n·2n＋2.‎ 错位相减法的适用范围及注意事项：‎ (1)适用范围：它主要适用于{an}是等差数列，{bn}是等比数列，求数列{anbn}的前n项和.‎ (2)注意事项：‎ ‎①利用“错位相减法”时，在写出Sn与qSn的表达式时，应注意使两式错对齐，以便于作差，正确写出(1－q)Sn的表达式.‎ ‎②利用此法时要注意讨论公比q是否等于1的情况.‎ ‎[再练一题]‎ ‎3.＋＋＋…＋＝________.‎ ‎【解析】　令Sn＝＋＋＋…＋，①‎ 则Sn＝＋＋＋…＋＋，②‎ 由①－②得，Sn＝＋＋＋…＋－ ‎＝－，‎ 得Sn＝2－－＝.‎ 9‎ ‎【答案】　 ‎1.数列 {2n－1}的前99项和为(　　)‎ A.2100－1 B.1－2100‎ C.299－1 D.1－299‎ ‎【解析】　数列{2n－1}为等比数列，首项为1，公比为2，故其前99项和为S99＝＝299－1.‎ ‎【答案】　C ‎2.等比数列{an}中，a3＝3S2＋2，a4＝3S3＋2，则公比q等于(　　) ‎ ‎【导学号：18082036】‎ A.2 B. C.4 D. ‎【解析】　a3＝3S2＋2，a4＝3S3＋2，等式两边分别相减得，a4－a3＝‎3a3即a4＝‎4a3，∴q＝4.‎ ‎【答案】　C ‎ ‎3.已知等比数列{an}中，q＝2，n＝5，Sn＝62，则a1＝________.‎ ‎【解析】　∵q＝2，n＝5，Sn＝62，‎ ‎∴＝62，‎ 即＝62，‎ ‎∴a1＝2.‎ ‎【答案】　2‎ ‎4.设等比数列{an}的前n项和为Sn，若S3＝‎3a3，则公比q＝________.‎ ‎【解析】　∵S3＝a1＋a2＋a3＝‎3a3，∴a1＋a2＝‎2a3，∵a1≠0，∴1＋q＝2q2，即2q2－q－1＝0，∴q＝－或1.‎ ‎【答案】　－或1‎ ‎5.已知{an}是公差为3的等差数列，数列{bn}满足b1＝1，b2＝，anbn＋1＋bn＋1＝nbn.‎ 9‎ ‎(1)求{an}的通项公式；‎ ‎(2)求{bn}的前n项和.‎ ‎【解】　(1)由已知，a1b2＋b2＝b1，b1＝1，b2＝，得a1＝2.‎ 所以数列{an}是首项为2，公差为3的等差数列，通项公式为an＝3n－1.‎ ‎(2)由(1)知anbn＋1＋bn＋1＝nbn，得bn＋1＝，‎ 因此{bn}是首项为1，公比为的等比数列.‎ 记{bn}的前n项和为Sn，‎ 则Sn＝＝－.‎ 9‎