高中数学（人教版必修5）配套练习：3-3二元一次不等式组与简单的线性规划问题第1课时 7页

第三章 3.3 第 1 课时 一、选择题 1．不在 3x＋2y＜6 表示的平面区域内的点是( ) A．(0,0) B．(1,1) C．(0,2) D．(2,0) [答案] D [解析] 将点的坐标代入不等式中检验可知，只有(2,0)点不满足 3x＋2y＜6. 2．不等式组 y＜x x＋y≤1 y≥3 ，表示的区域为 D，点 P1(0，－2)，点 P2(0,0)，则( ) A．P1∉D，P2∉D B．P1∉D，P2∈D C．P1∈D，P2∉D D．P1∈D，P2∈D [答案] A [解析] P1 点不满足 y≥3.P2 点不满足 y＜x.和 y≥3 ∴选 A． 3．已知点 P(x0，y0)和点 A(1,2)在直线 l：3x＋2y－8＝0 的异侧，则( ) A．3x0＋2y0>0 B．3x0＋2y0<0 C．3x0＋2y0<8 D．3x0＋2y0>8 [答案] D [解析] ∵3×1＋2×1－8＝－3<0，P 与 A 在直线 l 异侧，∴3x0＋2y0－8>0. 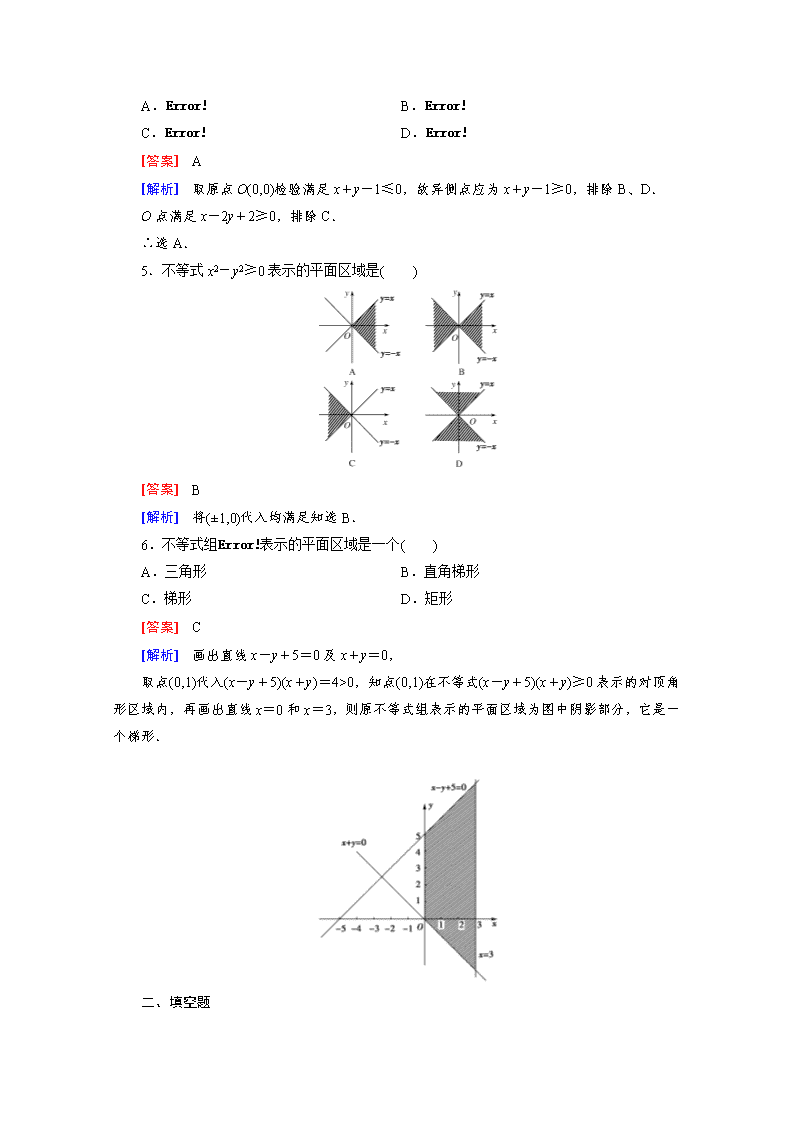4．图中阴影部分表示的区域对应的二元一次不等式组为( ) A． x＋y－1≥0 x－2y＋2≥0 B． x＋y－1≤0 x－2y＋2≤0 C． x＋y－1≥0 x－2y＋2≤0 D． x＋y－1≤0 x－2y＋2≥0 [答案] A [解析] 取原点 O(0,0)检验满足 x＋y－1≤0，故异侧点应为 x＋y－1≥0，排除 B、D． O 点满足 x－2y＋2≥0，排除 C． ∴选 A． 5．不等式 x2－y2≥0 表示的平面区域是( ) [答案] B [解析] 将(±1,0)代入均满足知选 B． 6．不等式组 x－y＋5x＋y≥0 0≤x≤3 表示的平面区域是一个( ) A．三角形 B．直角梯形 C．梯形 D．矩形 [答案] C [解析] 画出直线 x－y＋5＝0 及 x＋y＝0， 取点(0,1)代入(x－y＋5)(x＋y)＝4>0，知点(0,1)在不等式(x－y＋5)(x＋y)≥0 表示的对顶角 形区域内，再画出直线 x＝0 和 x＝3，则原不等式组表示的平面区域为图中阴影部分，它是一 个梯形． 二、填空题 7．已知 x，y 为非负整数，则满足 x＋y≤2 的点(x，y)共有________个． [答案] 6 [解析] 符合条件的点有(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(2,0)共 6 个． 8．用三条直线 x＋2y＝2,2x＋y＝2，x－y＝3 围成一个三角形，则三角形内部区域(不包括 边界)可用不等式表示为________． [答案] x＋2y＜2 2x＋y＞2 x－y＜3 三、解答题 9．画出不等式组 x＋y－6≥0 x－y≥0 y≤3 x＜5 表示的平面区域． [解析] 不等式 x＋y－6≥0 表示在直线 x＋y－6＝0 上及右上方的点的集合，x－y≥0 表 示在直线 x－y＝0 上及右下方的点的集合，y≤3 表示在直线 y＝3 上及其下方的点的集合，x ＜5 表示直线 x＝5 左方的点的集合，所以不等式组 x＋y－6≥0 x－y≥0 y≤3 x＜5 表示的平面区域为如图 阴影部分． 10．经过点 P(0，－1)作直线 l，若直线 l 与连结 A(1，－2)、B(2,1)的线段总有公共点，求 直线 l 的斜率 k 的取值范围． [解析] 由题意知直线 l 斜率存在，设为 k. 则可设直线 l 的方程为 kx－y－1＝0， 由题知：A、B 两点在直线 l 上或在直线 l 的两侧，所以有： (k＋1)(2k－2)≤0 ∴－1≤k≤1. 一、选择题 1．在平面直角坐标系中，若点 A(－2，t)在直线 x－2y＋4＝0 的上方，则 t 的取值范围是 ( ) A．(－∞，1) B．(1，＋∞) C．(－1，＋∞) D．(0,1) [答案] B [解析] 在直线方程 x－2y＋4＝0 中，令 x＝－2，则 y＝1，则点 P(－2,1)在直线 x－2y＋4 ＝0 上，又点(－2，t)在直线 x－2y＋4＝0 的上方，如图知，t 的取值范围是 t>1，故选 B． 2．不等式组 x－y＋1x＋y＋1≥0 －1≤x≤4 表示的平面区域是( ) A．两个三角形 B．一个三角形 C．梯形 D．等腰梯形 [答案] B [解析] 如图 ∵(x－y＋1)(x＋y＋1)≥0 表示如图(1)所示的对顶角形区域．且两直线交于点 A(－1,0)．故 添加条件－1≤x≤4 后表示的区域如图(2)． 3．不等式组 x－y＋6≥0 x＋y≥0 x≤3 表示的平面区域的面积是( ) A．18 B．36 C．72 D．144 [答案] B [解析] 作出平面区域如图． 交点 A(－3,3)、B(3、9)、C(3，－3)， ∴S△ABC＝1 2[9－(－3)]×[3－(－3)]＝36. 4．在平面直角坐标系中，若不等式组 x＋y－1≥0 x－1≤0 ax－y＋1≥0 (a 为常数)所表示的平面区域的面 积等于 2，则 a 的值为( ) A．－5 B．1 C．2 D．3 [答案] D [解析] 画出 x＋y－1≥0 x－1≤0 表示的平面区域如图，直线 l：y＝ax＋1 过定点(0,1)，由于 ax －y＋1≥0 与 x＋y－1≥0 x－1≤0 围成平面区域的面积为 2，∴a>0，令 x＝1 得 y＝a＋1，∴1 2 ×(a＋1)×1＝ 2，∴a＝3. 二、填空题 5．点 P(1，a)到直线 x－2y＋2＝0 的距离为3 5 5 ，且 P 在 3x＋y－3＞0 表示的区域内，则 a＝________. [答案] 3 [解析] 由条件知，|1－2a＋2| 5 ＝3 5 5 ，∴a＝0 或 3，又点 P 在 3x＋y－3＞0 表示的区域内， ∴3＋a－3＞0， ∴a＞0，∴a＝3. 6．不等式 x≤1 x－y＋1≥0 2x＋y＋2≥0 表示的平面区域的面积是________． [答案] 6 [解析] 作出平面区域如图△ABC，A(－1,0)、B(1,2)、C(1，－4)，S△ABC＝1 2·|BC|·d＝1 2 ×6×2 ＝6. (d 表示 A 到直线 BC 的距离．) 三、解答题 7．求由约束条件 x＋y≤5 2x＋y≤6 x≥0 y≥0 确定的平面区域的面积 S 和周长 C． [解析] 可行域如图所示，其四个顶点为 O(0,0)，B(3,0)，A(0,5)，P(1,4)．过点 P 作 y 轴 的垂线，垂足为 C，则 AC＝1，PC＝1， OC＝4，OB＝3，AP＝ 2，PB＝ 4－02＋1－32＝2 5，得周长 C＝AO＋BO＋AP＋PB ＝8＋ 2＋2 5. ∵S△ACP＝1 2AC·PC＝1 2 ， S 梯形 COBP＝1 2(CP＋OB)·OC＝8，∴面积 S＝S△ACP＋S 梯形 COBP＝17 2 . 8．画出不等式(x＋2y＋1)(x－y＋4)＜0 表示的平面区域． [解析] (x＋2y＋1)(x－y＋4)＜0 表示 x＋2y＋1 与 x－y＋4 的符号相反，因此原不等式等 价于两个不等式组 x＋2y＋1＞0， x－y＋4＜0， 与 x＋2y＋1＜0， x－y＋4＞0， 在同一直角坐标内作出两个不等式 组表示的平面区域，就是原不等式表示的平面区域． 在直角坐标系中画出直线 x＋2y＋1＝0 与 x－y＋4＝0，(画成虚线)取原点(0,0)可以判断． 不等式 x＋2y＋1＞0 表示直线 x＋2y＋1＝0 的右上方区域，x＋2y＋1＜0 表示直线 x＋2y ＋1＝0 的左下方区域；x－y＋4＜0 表示直线 x－y＋4＝0 的左上方区域，x－y＋4＞0 表示直线 x－y＋4＝0 的右下方区域． 所以不等式组表示的平面区域，即原不等式表示的平面区域如图所示．