2020_2021学年新教材高中数学第5章函数概念与性质5 9页

第2课时　函数的图象 学 习 目 标 核 心 素 养 ‎1．理解函数图象的概念，并能画出一些比较简单的函数的图象．(重点)‎ ‎2．能够利用图象解决一些简单的函数问题．(难点)‎ 通过学习本节内容培养学生的逻辑推理和直观想象核心素养．‎ 作出下列两个函数的的图象，并比较定义域和值域．‎ ‎(1)f(x)＝x2＋1，x∈{－1,0,1}；‎ ‎(2)f(x)＝x2＋1．‎ ‎1．函数的图象 将自变量的一个值x0作为横坐标，相应的函数值f(x0)作为纵坐标，就得到坐标平面上的一个点(x0，f(x0))．当自变量取遍函数定义域A中的每一个值时，就得到一系列这样的点．所有这些点组成的集合(点集)为{(x，f(x))|x∈A}，即{(x，y)|y＝f(x)，x∈A}，所有这些点组成的图形就是函数y＝f(x)的图象．‎ 思考1：函数的图象是否可以关于x轴对称？‎ ‎[提示]　不可以，如果关于x轴对称，则在定义域内一定存在一个自变量x0，有两个值和x0相对应，不符合函数的定义．‎ 思考2：函数y＝f(x)，x∈A的图象与直线x＝m(垂直于x轴的直线)的交点有几个？‎ ‎[提示]　0或1个，具体来说，当m∈A，由函数的定义，它们有唯一交点，当mA，它们无交点．‎ ‎2．作图、识图与用图 ‎(1)画函数图象常用的方法是描点作图，其步骤是列表、描点、连线．‎ ‎(2)正比例函数与一次函数的图象是一条直线，反比例函数的图象是双曲线，二次函数y＝ax2＋bx＋c(a≠0)的图象是抛物线，开口方向由a值符号决定，a>0，图象开口向上，a<0时，图象开口向下，对称轴为x＝－．‎ ‎1．思考辨析(正确的打“√”，错误的打“×”)‎ - 9 -‎ ‎(1)直线x＝a和函数y＝f(x)，x∈[m，n]的图象有1个交点． (　　)‎ ‎(2)设函数y＝f(x)的定义域为A，则集合P＝{(x，y)|y＝f(x)，x∈A}与集合Q＝{y|y＝f(x)，x∈A}相等，且集合P的图形表示的就是函数y＝f(x)的图象． (　　)‎ ‎[提示]　(1)若a∈[m，n]，则x＝a与y＝f(x)有一个交点，若a[m，n]，则x＝a与y＝f(x)无交点，故(1)错误．‎ ‎(2)Q是一个数集，P是一个点集，显然P≠Q，故(2)错误，但是P的图形表示的是函数y＝f(x)的图象．‎ ‎[答案]　(1)×　(2)×‎ ‎2．下列坐标系中的曲线或直线，能作为函数y＝f(x)的图象的有　　　　．(填序号)‎ ‎②④　[能作为函数的图象，必须符合函数的定义，即定义域内的每一个x只能有唯一的y与x对应，故②④可以，①③不可以．]‎ ‎3．函数y＝x＋1，x∈Z，且|x|<2的图象是　　　　．(填序号)‎ ‎③　[由题意知，函数的定义域是{－1,0,1}，值域是{0,1,2}，函数的图象是三个点，故③正确．]‎ 作函数的图象 ‎【例1】　作出下列函数的图象，并求函数的值域．‎ ‎(1)y＝3－x(|x|∈N*且|x|<3)；‎ ‎(2)y＝x2－2x＋2(－1≤x<2)．‎ ‎[思路点拨]　(1)中函数的定义域为{－2，－1,1,2}，图象为直线上的四个孤立点．‎ ‎(2)中函数图象为抛物线的一部分．‎ ‎[解]　(1)∵|x|∈N*且|x|<3，∴定义域为{－2，－1,1,2}，‎ - 9 -‎ ‎∴图象为直线y＝3－x上的4个孤立点，如图．‎ 由图象可知，值域为{5,4,2,1}．‎ ‎(2)y＝x2－2x＋2＝(x－1)2＋1(x∈[－1,2))，‎ 故函数图象为二次函数y＝(x－1)2＋1图象上在区间[－1,2)上的部分，如图，‎ x＝1时，y＝1，x＝－1时，y＝5，∴函数的值域为[1,5]．‎ ‎(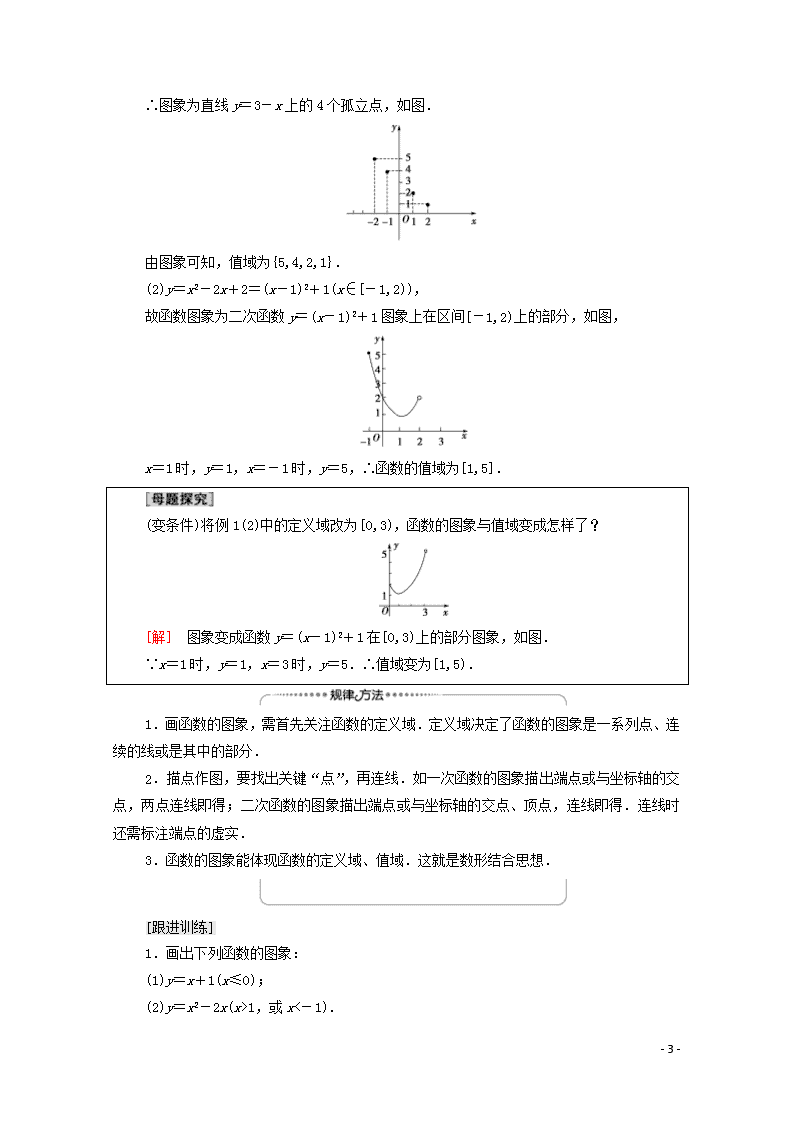变条件)将例1(2)中的定义域改为[0,3)，函数的图象与值域变成怎样了？‎ ‎[解]　图象变成函数y＝(x－1)2＋1在[0,3)上的部分图象，如图．‎ ‎∵x＝1时，y＝1，x＝3时，y＝5．∴值域变为[1,5)．‎ ‎1．画函数的图象，需首先关注函数的定义域．定义域决定了函数的图象是一系列点、连续的线或是其中的部分．‎ ‎2．描点作图，要找出关键“点”，再连线．如一次函数的图象描出端点或与坐标轴的交点，两点连线即得；二次函数的图象描出端点或与坐标轴的交点、顶点，连线即得．连线时还需标注端点的虚实．‎ ‎3．函数的图象能体现函数的定义域、值域．这就是数形结合思想．‎ ‎1．画出下列函数的图象：‎ ‎(1)y＝x＋1(x≤0)；‎ ‎(2)y＝x2－2x(x>1，或x<－1)．‎ - 9 -‎ ‎[解]　(1)y＝x＋1(x≤0)表示一条射线，图象如图①．‎ ‎(2)y＝x2－2x＝(x－1)2－1(x>1，或x<－1)是抛物线y＝x2－2x去掉－1≤x≤1之间的部分后剩余曲线．如图②．‎ ‎①　　　　　　②　‎ 函数图象的应用 ‎【例2】　已知函数f(x)＝－x2＋2x＋3的图象如图所示，据图回答以下问题：‎ ‎(1)比较f(－2)，f(0)，f(3)的大小；‎ ‎(2)求f(x)在[－1,2]上的值域；‎ ‎(3)求f(x)与y＝x的交点个数；‎ ‎(4)若关于x的方程f(x)＝k在[－1,2]内仅有一个实根，求k的取值范围．‎ ‎[思路点拨]　从图象上找到对应问题的切入点进而求解．‎ ‎[解]　(1)由题图可得f(－2)＝－5，f(0)＝3，f(3)＝0，‎ ‎∴f(－2)0时，y＝f(x＋a)可由y＝f(x)向左移动a个单位．当a<0时，y＝f(x＋a)可由y＝f(x)向右移动|a|个单位．‎ ‎4．若f(x)＝x2，写出y＝f(x)＋1和y＝f(x)－2的表达式，并在同一坐标系中作出三者的图象，观察其形状和位置的异同，由此，结合探究3，若已知f(x)的图象，如何得到y＝f(x)＋b的图象？‎ ‎[提示]　y＝f(x)＋1＝x2＋1，y＝f(x)－2＝x2－2，如图(3)．‎ 图(3)‎ 由y＝f(x)的图象得到y＝f(x)＋b的图象时，‎ 若b>0，把f(x)的图象向上移动b个单位得y＝f(x)＋b的图象．若b<0，把f(x)的图象向下移动|b|个单位得y＝f(x)＋b的图象．‎ - 9 -‎ ‎【例3】　用平移图象的方式作出y＝2＋的图象，并说明函数y＝2＋的值域．‎ ‎[思路点拨]　y＝2＋可以看作y＝先向右移动一个单位，又向上移动2个单位得到．‎ ‎[解]　‎ 从图象可以看出y＝2＋的值域为(－∞，2)∪(2，＋∞)．‎ 函数图象的平移变换 (1)左右平移：a＞0时，y＝f(x)的图象向左平移a个单位得到y＝f(x＋a)的图象；a＞0时，y＝f(x)的图象向右平移a个单位得到y＝f(x－a)的图象.‎ (2)上下平移：b＞0时，y＝f(x)的图象向上平移b个单位得到y＝f(x)＋b的图象；b＞0时，y＝f(x)的图象向下平移b个单位得到y＝f(x)－b的图象.‎ ‎3．已知函数y＝，将其图象向左平移a(a>0)个单位，再向下平移b(b>0)个单位后图象过坐标原点，则ab的值为　　　　．‎ ‎1　[y＝y＝y＝－b过(0,0)，故－b＝0，‎ ‎∴1－ab＝0，∴ab＝1．]‎ ‎1．作图象时一般应先确定函数的定义域，再在定义域内化简函数解析式，再列表描点，画出图象，并在画图象的同时注意一些关键点，如与坐标轴的交点、最高点或最低点，要分清这些关键点是实心点还是空心点．‎ ‎2．在利用图象研究函数时，准确地作出函数的图象是解决问题的关键，只有这样，对性质的研究才更准确．‎ ‎3．分析所给图象是不是函数图象的方法是：作一系列平行于y - 9 -‎ 轴的直线，若直线与图象最多只有一个交点，则该图象是函数的图象，否则就不是函数的图象．‎ ‎1．对于集合A＝{x|0≤x≤2}，B＝{y|0≤y≤3}，则由下列图形给出的对应f中，能构成从A到B的函数的是(　　)‎ D　[A中有一部分x值没有与之对应的y值；B中出现“一对多”的关系，不是函数关系；C中当x＝1时对应两个不同的y值，不构成函数；D中对应关系符合函数定义．]‎ ‎2．下列图形是函数y＝－|x|(x∈[－2,2])的图象的是(　　)‎ B　[y＝－|x|，当x＝2时，y＝－2，当x＝－2时，y＝－2．故选B．]‎ ‎3．函数y＝f(x)的图象如图所示．填空：‎ ‎(1)f(0)＝　　　　；‎ ‎(2)f(－1)＝　　　　；‎ ‎(3)f(－3)＝　　　　；‎ ‎(4)f(－2)＝　　　　；‎ ‎(5)f(2)＝　　　　；‎ ‎(6)f(4)＝　　　　；‎ ‎(7)若2