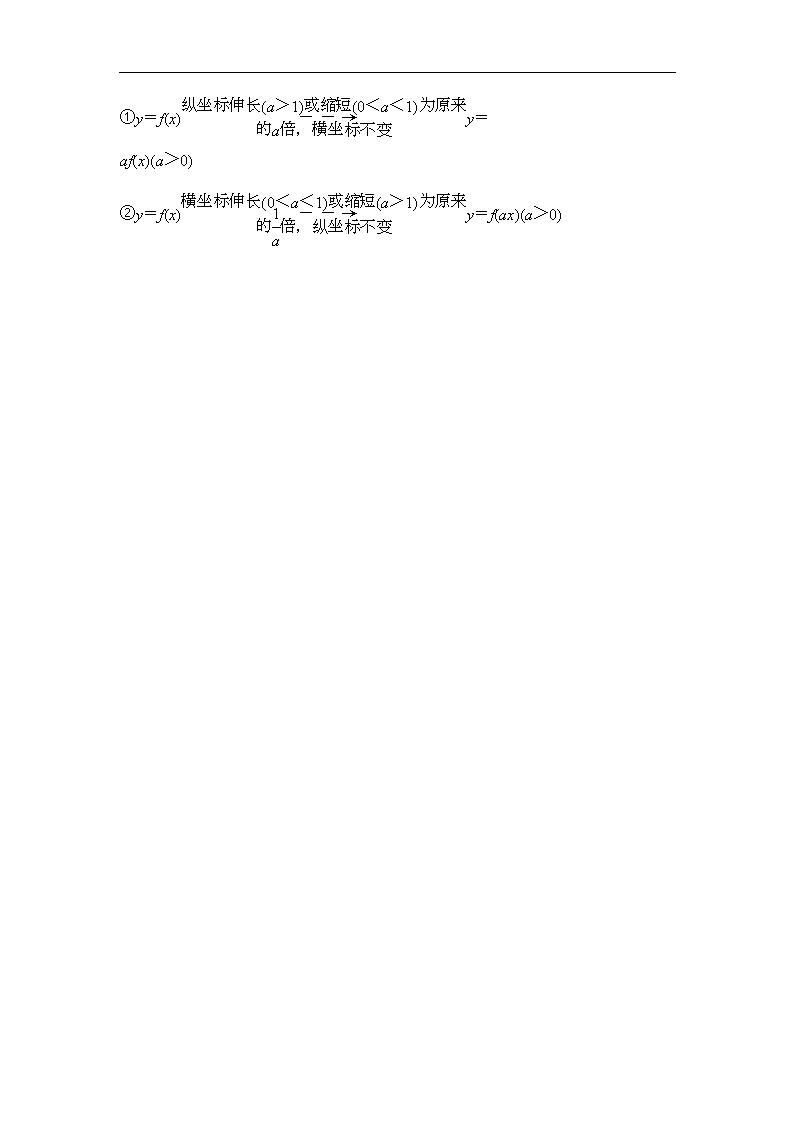高考数学专题复习教案： 函数的图象 3页

函数的图象 主标题：函数的图象 副标题：为学生详细的分析函数的图象的高考考点、命题方向以及规律总结。‎ 关键词：图象，变换，图象应用 难度：4‎ 重要程度：5‎ 考点剖析：‎ ‎1．在实际情境中，会根据不同的需要选择图象法、列表法、解析法表示函数．‎ ‎2．会运用函数图象理解和研究函数的性质，解决方程解的个数与不等式的解的问题.‎ 命题方向：常考查：①由函数的性质(如单调性、对称性、最值)及图象的变换选图象；②在解方程或不等式问题时，利用图象求交点个数或解集的范围，是高考考查的热点，常以选择题形式考查，难度中档．‎ 规律总结：1．掌握平移变换、伸缩变换、对称变换、翻折变换、周期变换等常用的方法技巧，来帮助我们简化作图过程．‎ ‎2．识图的要点：重点根据图象看函数的定义域、值域、奇偶性、单调性、特殊点(与x、y轴的交点，最高、最低点等)．‎ ‎3．识图的方法 ‎(1)定性分析法：对函数进行定性分析，从而得出图象的上升(或下降)的趋势，利用这一特征分析解决；‎ ‎(2)定量计算法：通过定量的计算来分析解决；‎ ‎(3)排除法：利用本身的性能或特殊点进行排除验证．‎ ‎4．研究函数性质时一般要借助于函数图象，体现了数形结合思想；‎ ‎5．方程解的问题常转化为两熟悉的函数图象的交点个数问题来解决．‎ ‎　　　‎ 知 识 梳 理 ‎1．函数的图象及作法 ‎2．图象变换 ‎(1)平移变换 ‎(2)对称变换 ‎①y＝f(x)y＝－f(x)；‎ ‎②y＝f(x)y＝f(－x)；‎ ‎③y＝f(x)y＝－f(－x)；‎ ‎④y＝ax(a＞0且a≠1)y＝logax(a＞0且a≠1)．‎ ‎(3)翻折变换 ‎①y＝f(x)y＝|f(x)|.‎ ‎②y＝f(x)y＝f(|x|)．‎ ‎(4)伸缩变换 ‎①y＝f(x)y＝‎ af(x)(a＞0)‎ ‎②y＝f(x)y＝f(ax)(a＞0)‎