2020年高中数学新教材同步必修第一册 第3章3．3 幂函数 13页

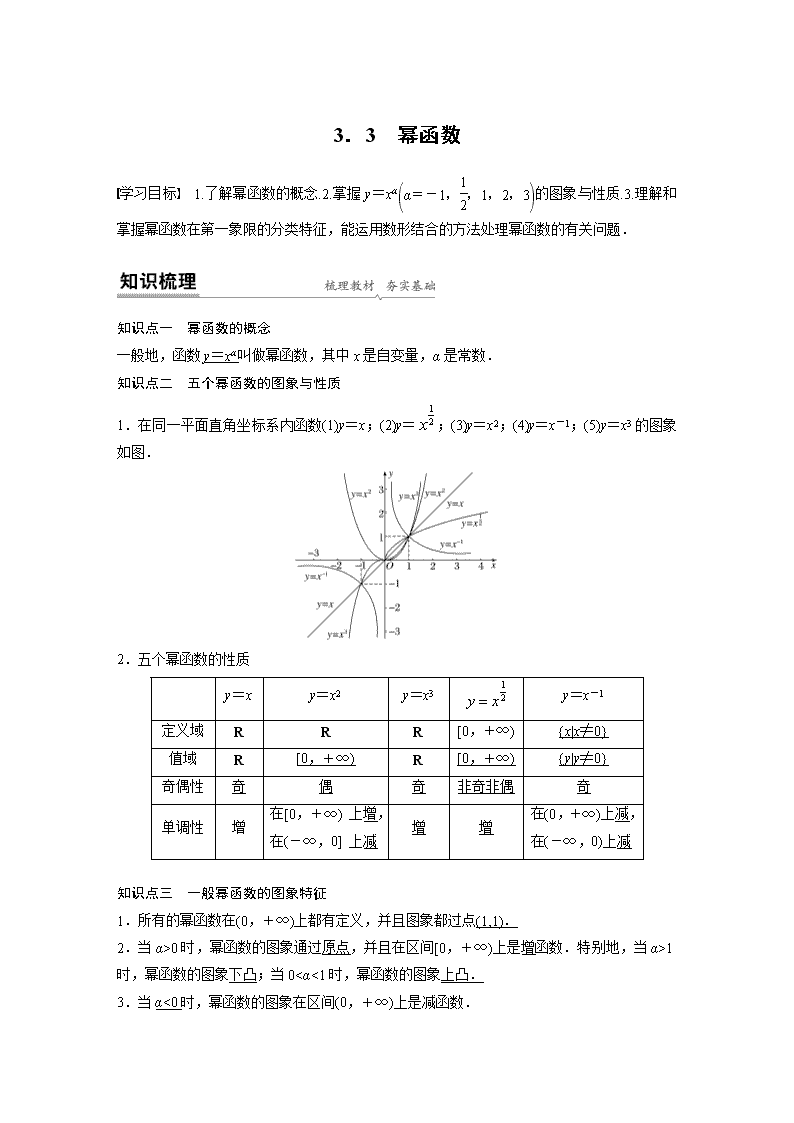
3．3 幂函数 学习目标 1.了解幂函数的概念.2.掌握 y＝xα α＝－1，1 2 ，1，2，3 的图象与性质.3.理解和 掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题． 知识点一 幂函数的概念 一般地，函数 y＝xα叫做幂函数，其中 x 是自变量，α是常数． 知识点二 五个幂函数的图象与性质 1．在同一平面直角坐标系内函数(1)y＝x；(2)y＝ 1 2x ；(3)y＝x2；(4)y＝x－1；(5)y＝x3 的图象如 图． 2．五个幂函数的性质 y＝x y＝x2 y＝x3 1 2y x y＝x－1 定义域 R R R [0，＋∞) {x|x≠0} 值域 R [0，＋∞) R [0，＋∞) {y|y≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 在[0，＋∞) 上增， 在(－∞，0] 上减 增 增 在(0，＋∞)上减， 在(－∞，0)上减 知识点三 一般幂函数的图象特征 1．所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)． 2．当α>0 时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1 时， 幂函数的图象下凸；当 0<α<1 时，幂函数的图象上凸． 3．当α<0 时，幂函数的图象在区间(0，＋∞)上是减函数． 4．幂指数互为倒数的幂函数在第一象限内的图象关于直线 y＝x 对称． 5．在第一象限，作直线 x＝a(a>1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指 数按从小到大的顺序排列． 预习小测 自我检验 1．下列函数中不是幂函数的是________． ①y＝x0； ②y＝x3； ③y＝2x； ④y＝x－1. 答案 ③ 2．设α∈ －1，1，1 2 ，3 ，则使函数 y＝xα的定义域为 R 且为奇函数的所有α的值为________． 答案 1,3 解析 当幂函数为奇函数时，α＝－1,1,3， 又函数的定义域为 R， 所以α≠－1，所以α＝1,3. 3．当 x∈(0,1)时，x2________x3.(填“>”“＝”或“<”) 答案 > 4．已知幂函数 f(x)＝xα图象过点 2， 2 2 ，则 f(4)＝________. 答案 1 2 一、幂函数的概念 例 1 (1)下列函数： ①y＝x3；②y＝ 1 2 x；③y＝4x2；④y＝x5＋1；⑤y＝(x－1)2；⑥y＝x；⑦y＝ax(a>1)．其中幂函 数的个数为( ) A．1 B．2 C．3 D．4 答案 B 解析 幂函数有①⑥两个． (2)已知 22 2( )2 2 2 3my m m x n－＝ ＋ － ＋ － 是幂函数，求 m，n 的值． 考点 幂函数的概念 题点 由幂函数定义求参数值 解 由题意得 m2＋2m－2＝1， 2n－3＝0， 解得 m＝－3， n＝3 2 或 m＝1， n＝3 2. 所以 m＝－3 或 1，n＝3 2. 反思感悟 判断函数为幂函数的方法 (1)自变量 x 前的系数为 1. (2)底数为自变量 x. (3)指数为常数． 跟踪训练 1 (1)已知幂函数 f(x)＝k·xα的图象过点 1 2 ， 2 2 ，则 k＋α等于( ) A.1 2 B．1 C.3 2 D．2 答案 C 解析 由幂函数的定义知 k＝1. 又 f 1 2 ＝ 2 2 ，所以 1 2 α＝ 2 2 ， 解得α＝1 2 ，从而 k＋α＝3 2. (2)已知 f(x)＝ax2a＋1－b＋1 是幂函数，则 a＋b 等于( ) A．2 B．1 C.1 2 D．0 答案 A 解析 因为 f(x)＝ax2a＋1－b＋1 是幂函数， 所以 a＝1，－b＋1＝0， 即 a＝1，b＝1，则 a＋b＝2. 二、幂函数的图象及应用 例 2 (1)已知幂函数 f(x)＝xα的图象过点 P 2，1 4 ，试画出 f(x)的图象并指出该函数的定义域 与单调区间． 解 因为 f(x)＝xα的图象过点 P 2，1 4 ， 所以 f(2)＝1 4 ，即 2α＝1 4 ， 得α＝－2，即 f(x)＝x－2， f(x)的图象如图所示， 定义域为(－∞，0)∪(0，＋∞)，单调减区间为(0，＋∞)，单调增区间为(－∞，0)． (2)下列关于函数 y＝xα与 y＝αx α∈ －1，1 2 ，2，3 的图象正确的是( ) 答案 C 反思感悟 (1)幂函数图象的画法 ①确定幂函数在第一象限内的图象：先根据α的取值，确定幂函数 y＝xα在第一象限内的图象． ②确定幂函数在其他象限内的图象：根据幂函数的定义域及奇偶性确定幂函数 f(x)在其他象 限内的图象． (2)解决与幂函数有关的综合性问题的方法 首先要考虑幂函数的概念，对于幂函数 y＝xα(α∈R)，由于α的取值不同，所以相应幂函数的 单调性和奇偶性也不同．同时，注意分类讨论思想的应用． 跟踪训练 2 (1)如图所示，C1，C2，C3 为幂函数 y＝xα在第一象限内的图象，则解析式中的 指数α依次可以取( ) A.4 3 ，－2，3 4 B．－2，3 4 ，4 3 C．－2，4 3 ，3 4 D.3 4 ，4 3 ，－2 答案 C (2)在同一坐标系内，函数 y＝xa(a≠0)和 y＝ax－1 a 的图象可能是( ) 考点 幂函数的图象 题点 幂函数有关的知图选式问题 答案 C 解析 选项 A 中，幂函数的指数 a<0，则直线 y＝ax－1 a 应为减函数，A 错误； 选项 B 中，幂函数的指数 a>1，则直线 y＝ax－1 a 应为增函数，B 错误； 选项 D 中，幂函数的指数 a<0，则－1 a>0，直线 y＝ax－1 a 在 y 轴上的截距为正，D 错误． 三、比较幂值的大小 例 3 比较下列各组数的大小． (1) 2 5 0.5 与 1 3 0.5； (2) －2 3 －1 与 －3 5 －1； (3) 1 33 2      与 1 41 3      . 解 (1)因为幂函数 y＝x0.5 在(0，＋∞)上是单调递增的， 又2 5>1 3 ，所以 2 5 0.5> 1 3 0.5. (2)因为幂函数 y＝x－1 在(－∞，0)上是单调递减的， 又－2 3<－3 5 ，所以 －2 3 －1> －3 5 －1. (3)因为 1 3y x 在(0，＋∞)上是单调递增的， 所以 1 13 33 2 1       ＝1， 又 1 4y x 在(0，＋∞)上是单调递增的， 所以 1 14 41 3 1       ＝1，所以 1 3 1 43 2 1 3        . 反思感悟 此类题在构建函数模型时要注意幂函数的特点：指数不变．比较大小的问题主要 是利用函数的单调性，特别是要善于应用“搭桥”法进行分组，常数 0 和 1 是常用的中间量． 跟踪训练 3 比较下列各组数的大小： (1) 5 23  和 5 23.1  ； (2) 2 54.1 ， 2 33.8  和 3 51.9 . 解 (1)函数 y＝ 5 2x  在(0，＋∞)上为减函数， 又 3<3.1，所以 5 2 5 2 33 .1   . (2) 5 2 5 2 1 14.1  ＝； 2 3 2 30 1 1;3.8       3 51.9 0,  所以  2 2 3 5 3 5 3.8 1 .1.9 4.    幂函数性质的应用 典例 已知幂函数 y＝x3m－9 (m∈N*)的图象关于 y 轴对称且在(0，＋∞)上单调递减，求满足    3 331 2 mm a a   的 a 的取值范围． 考点 幂函数的性质 题点 利用幂函数的性质解不等式 解 因为函数在(0，＋∞)上单调递减，所以 3m－9<0， 解得 m<3.又因为 m∈N*，所以 m＝1,2. 因为函数的图象关于 y 轴对称， 所以 3m－9 为偶数，故 m＝1. 则原不等式可化为   1 1 33 3 2 .1 aa    因为 1 3y x   在(－∞，0)，(0，＋∞)上单调递减， 所以 a＋1>3－2a>0 或 3－2a 3 2 2 D． 7 87 88 1 9       答案 A 3．函数 y＝x－3 在区间[－4，－2]上的最小值是________． 答案 －1 8 解析 因为函数 y＝x－3＝1 x3 在(－∞，0)上单调递减， 所以当 x＝－2 时，ymin＝(－2)－3＝ 1 －23 ＝－1 8. 4．若幂函数   22 2 31( ) m mf x m m x － －＝ － － 在(0，＋∞)上是减函数，则实数 m＝________. 答案 2 解析 令 m2－m－1＝1，得 m＝2 或 m＝－1. 当 m＝2 时，m2－2m－3＝－3 符合要求． 当 m＝－1 时，m2－2m－3＝0 不符合要求． 故 m＝2. 5．先分析函数 2 3y x 的性质，再画出其图象． 解 2 3 23y x x  ，定义域为 R，在[0，＋∞)上是上凸的增函数，且是偶函数，故其图象 如下： 1．知识清单： (1)幂函数的定义． (2)几个常见幂函数的图象． (3)幂函数的性质． 2．方法归纳： (1)运用待定系数法求幂函数的解析式． (2)根据幂函数的图象研究幂函数的性质即数形结合思想． 3．常见误区：对幂函数形式的判断易出错，只有形如 y＝xα(α为常数)为幂函数，其它形式都 不是幂函数． 1．下列函数中是幂函数的是( ) A．y＝x4＋x2 B．y＝10x C．y＝1 x3 D．y＝x＋1 考点 幂函数的概念 题点 判断函数是否为幂函数 答案 C 解析 根据幂函数的定义知，y＝1 x3 是幂函数， y＝x4＋x2，y＝10x，y＝x＋1 都不是幂函数． 2．下列幂函数中，既是偶函数，又在区间(0，＋∞)上单调递减的是( ) A．y＝x－2 B．y＝x－1 C．y＝x2 D．y＝ 1 3x 答案 A 解析 其中 y＝x－2 和 y＝x2 是偶函数，y＝x－1 和 y＝ 1 3x 不是偶函数，故排除选项 B，D，又 y ＝x2 在区间(0，＋∞)上单调递增，不合题意，y＝x－2 在区间(0，＋∞)上单调递减，符合题意， 故选 A. 3．已知 f(x)＝ 1 2x ，若 02.5α，则α的取值范围是________． 答案 α<0 解析 因为 0<2.4<2.5，而 2.4α>2.5α， 所以 y＝xα在(0，＋∞)上为减函数．故α<0. 7．已知 m＝(a2＋3)－1(a≠0)，n＝3－1，则 m 与 n 的大小关系为________． 答案 m3>0，f(x)在(0，＋∞)上是减函数， 则 f(a2＋3)g(x)；f(x)＝g(x)；f(x)g(x)； 当 x＝1 时，f(x)＝g(x)；当 x∈(0,1)时，f(x)